Codeforces Round 924 (Div. 2)

E - Modular Sequence

题意

给定 \(n, x, y, s\)，求是否有长为 \(n\) 的一个数列 \(\{a\}\) 满足 \(a_1 = x\) 且 \(\forall i > 1 : a_i = a_{i - 1} + y \lor a_i = a_{i - 1} \bmod y\) 且 \(\sum\limits_{i = 1}^{n} a_i = s\)。

\(\sum n, \sum s \le 2 \times 10^5\)

题解

观察到对任意的 \(i\) 都有 \(a_i \equiv x \pmod{y}\)，于是可以先给 \(s\) 减去 \(n \times (x \bmod y)\)，剩下的部分一定是非负的 \(y\) 的倍数，否则显然不合法。

令 \(c = \dfrac{s - n \times (x \bmod y)}{y}, c_0 = \left\lfloor\dfrac{x}{y}\right\rfloor\)，于是问题转化为：求一个数列 \(b\) 满足第一项为 \(c_0\)，和为 \(c\)，每一项要么等于前一项加一，要么为 \(0\)（这相当于若干个公差为 \(1\) 的等差数列拼起来）。

直接考虑每个位置做 DP 最少也要 2D 的状态（位置，上一个的值），但是观察到值域很小，于是不妨交换状态和答案，设 \(dp_i\) 表示得到和为 \(i\) 的数列 \(b\) 需要的最小长度。由于可以在后面补 \(0\)，所以有解的充要条件为 \(dp_c \le n\)。

转移考虑枚举下一个等差数列的长度，若当前计算 \(dp_i\)，枚举的长度为 \(j\)，则显然需要满足 \(i \ge \dfrac{j(j - 1)}{2}\)，于是有 \(j \le O(\sqrt{i})\)，那么暴力转移即可做到 \(O(s \sqrt{s})\)。

由于第一个等差数列的首项比较特别，但是仅有它一个特别的，于是先暴力枚举它的长度给 \(dp\) 数组赋初值即可。

于是处理一组数据的时间复杂度为 \(O(n + s\sqrt{s})\)。

Submission

F - Digital Patterns

题意

给定 \(a_1, a_2, \dots, a_n\) 和 \(b_1, b_2, \dots, b_n\)，构造 \(n\) 行 \(m\) 列的矩阵满足 \((i, j)\) 处的值为 \(a_i + b_j\)。定义答案为满足方阵中任意一条边两侧的数不同的子方阵个数。每次修改是对 \(a\) 或 \(b\) 中的一段区间加 \(x\)，求每次修改后和最初时的答案。

题解

首先考虑不带修怎么求。观察到 \((i, j)\) 处和 \((i, j + 1)\) 处值相同的充要条件为 \(b_j = b_{j + 1}\)，\((i, j)\) 和 \((i + 1, j)\) 同理，于是相当于在相邻且相同的两行中间切开，相邻且相同的两列中间切开，对得到的若干子矩阵求答案并求和。

文字有点抽象，可以看样例：

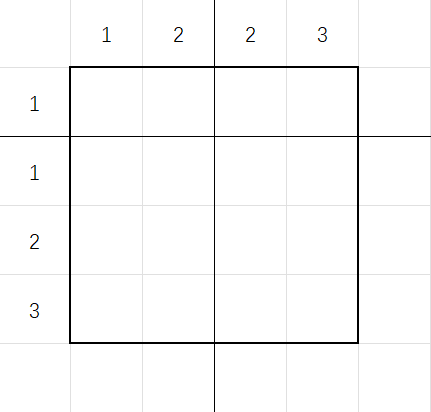
设 \(f(n, m)\) 表示 \(n \times m\) 矩阵的子方阵数目，则样例 \(1\) 的答案为 \(f(1, 2) + f(1, 2) + f(3, 2) + f(3, 2)\)。

考虑如何计算 \(f\)，容易枚举方阵大小计算，不失一般性，设 \(n \le m\)：

\[\begin{aligned} f(n, m) = \sum\limits_{i = 1}^{n} (n - i + 1) (m - i + 1) \end{aligned} \]

这个式子显然不好弄，我们需要更好算的式子，容易发现它是一个三次多项式，可以大力展开：

\[\begin{aligned} f(n, m) &= \sum\limits_{i = 1}^{n} (n - i + 1) (m - i + 1) \\ &= \sum\limits_{i = 1}^{n} i (m - n + i) \\ &= \sum\limits_{i = 1}^{n} (m - n) i + i ^ 2 \\ &= (m - n) \left(\sum\limits_{i = 1}^{n} i \right) + \left(\sum\limits_{i = 1}^{n} i^2 \right) \\ &= (m - n) \dfrac{n (n + 1)}{2} + \dfrac{n (n + 1) (2n + 1)}{6} \\ &= m \dfrac{n^2 + n}{2} + \dfrac{-n^3 + n}{6} \end{aligned} \]

这个式子已经很简洁了。注意到只要对 \(n, m\) 的大小分类讨论，并维护出它们对应的 \(0\) 到 \(3\) 次和就可以快速对一个固定的 \(m\) 求出 \(\sum\limits_{i} f(n_i, m)\)，固定的 \(n\) 同理。

于是可以先对行列分别按相等位置分段，对值域开数据结构维护一个方向的长度的 \(0\) 到 \(3\) 次和，并依次添加另一个方向的长度，同时计算答案即可。

对于修改，首先发现区间修改是骗人的，因为我们关注的只是相邻元素是否相同，于是区间修改相当于改变左右端点处的相等情况，相当于对相等情况的两次单点改。

单点改可以等价于先删再加，删除和添加都可以根据上面的式子讨论大小关系后求出答案变化量。删除和添加的区间长度容易用 set 维护。

至此我们得到了一个常数巨大的 \(O(n \log n + q \log n)\) 的做法，写得一般的线段树好像还过不了（zkw 可过），不过 \(0\) 到 \(3\) 次和可以用 \(8\) 个 BIT 分别维护，区间加可以用两个 BIT 维护差分（只有单点查），这里 set 因为操作少所以还不算瓶颈。

Submission