线段树优化建图

常见线段树 \(trick\)

一般是区间/点向区间/点连边

线段树的本质就是区间向点的映射，我们利用这一点优化

P6348 [PA2011] Journeys

我们建立一颗入树和出树，如下图

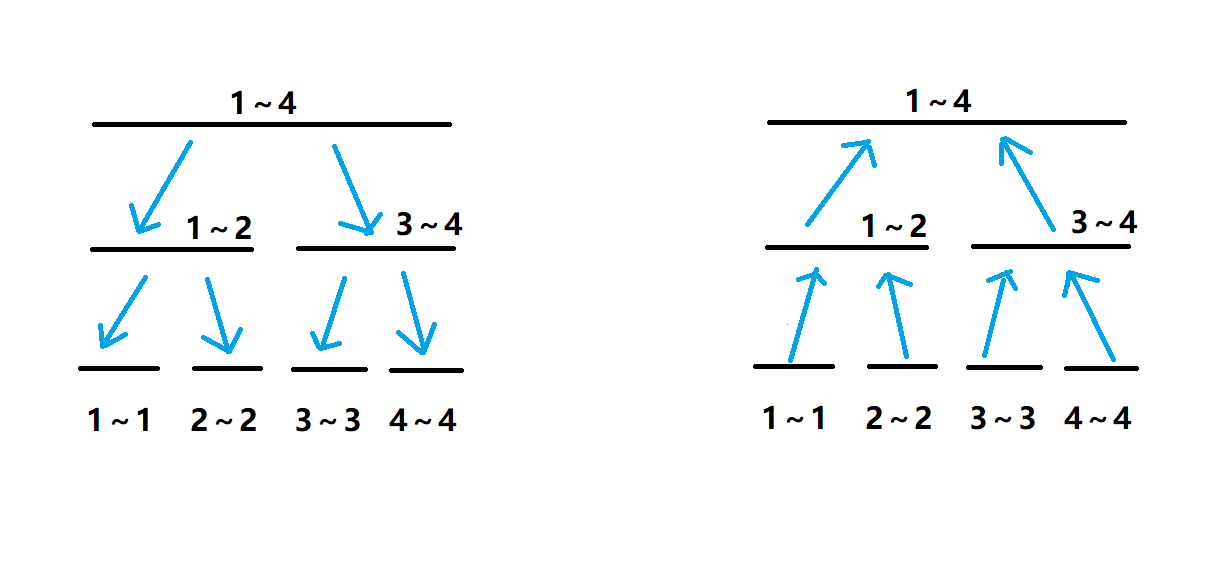
左边是出树， 右边是入树， 蓝色边权为 \(0\)

当我们需要从 \([a,b] \to [c,d]\) 建边，就 对 \([1,2]\) \([3,4]\) 建立两个虚点，虚点之间连边

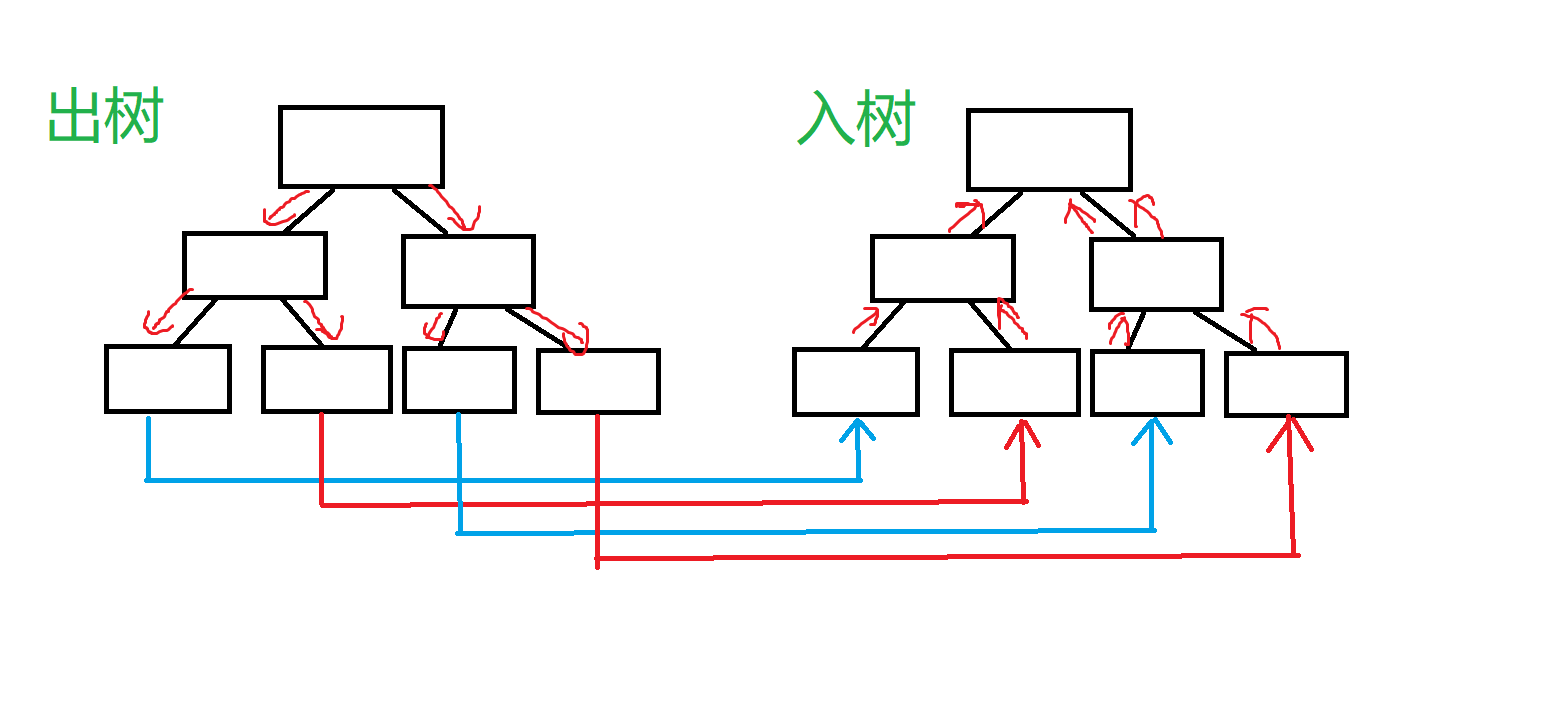
#include<bits/stdc++.h>
#define int long long
#define pt putchar(' ')
#define nl puts("")
#define pi pair<int,int>
#define pb push_back
#define go(it) for(auto &it:as[x])
using namespace std;

const int N=5e6+10;
int n,m,S,a,b,c,d,cnt,R1,R2;
int D[N],p[N];
struct node{int lc,rc;}tr[N];
vector<pi> as[N];

int fr(){
    int x=0,flag=1;
    char ch=getchar();
    while(ch<'0' || ch>'9'){
        if(ch=='-') flag=-1;
        ch=getchar();
    }
    while(ch>='0' && ch<='9'){
        x=x*10+(ch-'0');
        ch=getchar();
    }
    return x*flag;
}
void fw(int x){
	if(x<0) putchar('-'),x=-x;
    if(x>9) fw(x/10);
    putchar(x%10+'0');
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}

int build_Out(int ql,int qr)
{
	if(ql==qr) return ql;
	int x=++cnt,mid=(ql+qr)>>1;
	tr[x]={build_Out(ql,mid),build_Out(mid+1,qr)};
	as[x].pb({tr[x].lc,0}),as[x].pb({tr[x].rc,0});
	return x;
}

int build_In(int ql,int qr)
{
	if(ql==qr) return ql;
	int x=++cnt,mid=(ql+qr)>>1;
	tr[x]={build_In(ql,mid),build_In(mid+1,qr)};
	as[tr[x].lc].pb({x,0}),as[tr[x].rc].pb({x,0});
	return x;
}

void modify(int ql,int qr,int l,int r,int idx,int op)
{
	if(ql<=l && qr>=r)
	{
		if(!op) as[idx].pb({cnt,0});
		else as[cnt].pb({idx,0});
		return;
	}
	
	int mid=(l+r)>>1;
	if(ql<=mid) modify(ql,qr,l,mid,tr[idx].lc,op);
	if(qr>mid) modify(ql,qr,mid+1,r,tr[idx].rc,op);
}

void insert(int a,int b,int c,int d)
{
	int p=++cnt;modify(a,b,1,n,R2,0);
	int q=++cnt;modify(c,d,1,n,R1,1);
	as[p].pb({q,1});
}

void dij()
{
	priority_queue<pi,vector<pi>,greater<pi>> q;
	memset(D,0x3f,sizeof D);
	D[S]=0;
	q.push({0,S});
	
	while(q.size())
	{
		auto t=q.top();
		q.pop();
		
		int x=t.second;
		if(p[x]) continue;
		p[x]=1;
		
		go(it)
		{
			int v=it.first,w=it.second;
			if(D[v]>D[x]+w)
			{
				D[v]=D[x]+w;
				q.push({D[v],v});
			}
		}
	}
	for(int i=1;i<=n;i++) fw(D[i]),nl;
}

signed main()
{
	cnt=n=fr(),m=fr(),S=fr();
	R1=build_Out(1,n),R2=build_In(1,n);
	for(int i=1;i<=m;i++)
	{
		a=fr(),b=fr(),c=fr(),d=fr();
		insert(a,b,c,d),insert(c,d,a,b);
	}
	dij();
	return 0;
}