网络流学习

网络流

概念：

1.流网络

有向图 \(G=(V,E)\)，\(n\) 个点，\(m\) 条边，源点 \(s\)，汇点 \(t\)，定义 \(c\ (u,v)\) 为边 \((u,v)\) 的容量，定义 \(f\ (u,v)\) 表示边 \((u,v)\) 的流量。这样的图就是一个流网络

2.可行流 \(f\)

需满足两个条件：
（1）满足容量限制：流量 \(\leq\) 容量
\(\hspace{1cm}0\leq f\ (u,v) \leq c\ (u,v)\)

（2）流量守恒：对于每个点（除了源点和汇点），流进去多少等于流出来多少
\(\hspace{1cm}\forall x \neq {s\ or\ t}, \quad \sum_{(u,x) \in E}\ f(u,x) = \sum_{(x,v) \in E}\ f(x,v)\)

最大流：最大的可行流

3.\(|f|\)

从源点流向外面的流量

\(|f|=\sum_{(s,\ u) \in E}\ f(s,u)-\sum_{(u,s) \in E}\ f(u,s)\)
\(\hspace{4cm} \small（流向源点的，一般没有）\)

4.残留网络 \(G_f\)

\(V_f=V,\ E_f=E+E_{反向边}\)

\(c'\ (u,v)=\begin{cases}c(u,v)-f(u,v), & (u,v) \in E \\f(v,u), & (v,u) \in E_{\text{反向边}}\end{cases}\)

性质：

对于 \(G\) 的 \(f\) 和 \(G_f\) 的 \(f'\)
\(f+f'\) 也是 \(G\) 的一个可行流，且 \(|f+f'|=|f|+|f'|\)

其中 \(f+f'\) 的计算方式为：如果两条边方向一样相加，不一样则原边减去反向边

5.增广路径

在 \(G_f\) 中如果能从源点沿着容量大于 \(0\) 的边走到汇点，那么这条路径就是一个增广路径

推论：
如果对于一个可行流，它的残留网络有增广路径，那么它肯定不是最大流

6.割

把 \(V\) 分为 \(S,T\) 两部分，\(s\in S\)，\(t\in T\)，且 \(S\cap T=\emptyset\)，\(S\cup T=V\)，则称为一个割

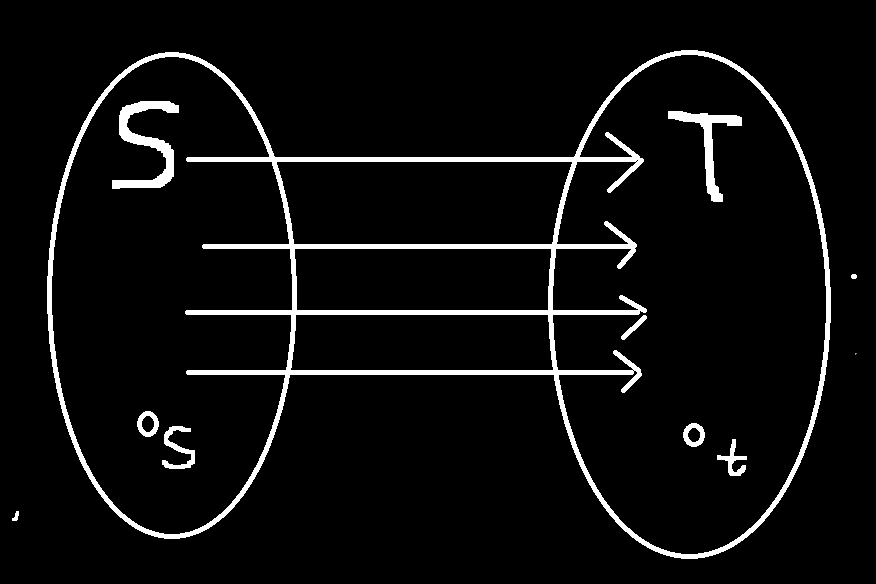
割的容量：\(c(S,T)=\sum_{u\in S}\sum_{v\in T}\ c(u,v)\)
割的流量：\(f(S,T)=\sum_{u\in S}\sum_{v\in T}\ f(u,v)-\sum_{u\in T}\sum_{v\in S}\ f(u,v)\)

最小割：最小容量割

推论：
\(\because\ f(S,T)=\sum_{u\in S}\sum_{v\in T}\ f(u,v)-\sum_{u\in T}\sum_{v\in S}\ f(u,v)\)
\(\therefore\ f(S,T)\leq \sum_{u\in S}\sum_{v\in T}\ f(u,v)\)
又\(\ \because f(u,v)\leq c(u,v)\)
\(\therefore f(S,T)\leq \sum_{u\in S}\sum_{v\in T}\ c(u,v)\)
又\(\ \because |f|=f(S,T)\)
\(=> |f|\leq c(S,T)\)

最大流最小割定理

（1）可行流 \(f\) 是最大流
（2）可行流 \(f\) 的 \(G_f\) 中不存在增广路
（3）存在某个割 \([S,T]\)，\(|f|=c(S,T)\)

三者等价，即由一个可以推出另外两个

\(EK\) 算法

不停的找一条增广路，然后更新残留网络，直到没有增广路

找到一条增广路以后，记这条路径上的最小的流量为 \(f_0\)，那么每条正向边的剩余流量就减去 \(f_0\)，反向边就加上 \(f_0\)
在记录增广路这条路径时，可以用 \(pre[\ ]\) 数组记录每个点的前驱

namespace Solution{
    int n, m, s, t;
    int head[maxn], cnt = 1;
    struct Edge{
        int nxt, to, val;
    } e[maxn];
    void add_Edge(int u, int v, int w){
        cnt++;
        e[cnt].to = v;
        e[cnt].nxt = head[u];
        e[cnt].val += w;
        head[u] = cnt;
        cnt++;
        e[cnt].to = u;
        e[cnt].nxt = head[v];
        e[cnt].val = 0;
        head[v] = cnt;
    }
    int cmin[maxn], pre[maxn];
    bool vis[maxn];
    bool bfs(){
        memset(vis, 0, sizeof(vis));
        vis[s] = 1;
        queue<int> q;
        q.push(s);
        cmin[s] = INF;
        while (!q.empty()){
            int u = q.front();
            q.pop();
            FOR (i, u){
                int to = e[i].to;
                if (!vis[to] && e[i].val){
                    vis[to] = 1;
                    pre[to] = i;
                    cmin[to] = min(cmin[u], e[i].val);
                    q.push(to);
                    if (to == t) return true;
                }
            }
        }
        return false;
    }
    int EK(){
        int ans = 0;
        while (bfs()){
            ans += cmin[t];
            for (int i = t; i != s; i =  e[pre[i] ^ 1].to){
                e[pre[i]].val -= cmin[t];
                e[pre[i] ^ 1].val += cmin[t];
            }
        }
        return ans;
    }
    void Main(){
        memset(head, -1, sizeof(head));
	    cin >> n >> m >> s >> t;
        For (i, 1, m){
            int x, y, z;
            cin >> x >> y >> z;
            add_Edge(x, y, z);
        }
        cout << EK() << endl;
    }
}

时间复杂度：\(\operatorname{O}(nm^2)\)，实际远低于 \(nm^2\)
可以处理 \(1000-10000\) 的图

\(Dinic\) 算法

其实就是对 \(EK\) 的一个优化，\(Ek\) 算法中每次都可能遍历整个残留网络，但是只找到了一条增广路，\(Dicnic\) 算法就是在其基础上每次找到所有的增广路。

怎么每次找到多条增广路？
可以先 \(bfs\) 建分层图，这样再每次 \(dfs\) 的时候，从 \(s\) 开始，每次向下面一层找一个点直到点 \(t\)，然后再一层一层回溯回去，继续找这一层其他的点，就可以找到所有的增广路

然后就是一样的更新残留网络

当前弧优化：
如果当前点之后到不了汇点或者到汇点的路径上存在点流量 \(\leq 0\)，那么就说明肯定这条路就不能再走了，下次就不用遍历这个分支，用 \(cur\) 数组记录，这样子下一次访问的时候就可以直接跳过这个

对于一个节点 \(x\)，当它在 \(DFS\) 中走到了第 \(i\) 条边时，前 \(i−1\) 条弧到汇点的流一定已经被流满而没有可行的路线了，
那么当下一次再访问 \(x\) 节点时，前 \(i−1\) 条弧就没有任何意义了

\(sum\) 表示当前节点 \(u\) 能接受的最大的流量，即从源点 \(s\) 到 \(u\) 路径上剩余的可分配的流量
\(res\) 表示从当前节点 \(u\) 实际推出去的流量
\(Min\) 表示当前剩余的最小流量

namespace Solution{
    int n, m, s, t;
    struct Edge{
        int nxt, to, val;
    } e[MAXN];
    int head[maxn], cnt = 1;
    void add_Edge(int u, int v, int w){
        cnt++;
        e[cnt].nxt = head[u];
        e[cnt].to = v;
        e[cnt].val += w;
        head[u] = cnt;
        cnt++;
        e[cnt].nxt = head[v];
        e[cnt].to = u;
        e[cnt].val = 0;
        head[v] = cnt;
    }
    int depth[maxn], cur[maxn];
    bool vis[maxn];
    bool bfs(){
        memset(depth, -1, sizeof(depth));
        depth[s] = 0;
        queue<int> q;
        q.push(s);
        cur[s] = head[s];
        while (!q.empty()){
            int u = q.front(); q.pop();
            FOR (i, u){
                int to = e[i].to;
                if (e[i].val && depth[to] == -1){
                    depth[to] = depth[u] + 1;
                    q.push(to);
                    cur[to] = head[to];
                    if (to == t) return true;
                }
            }
        }
        return false;
    }
    int dfs(int u, int sum){
        if (u == t) return sum;
        int Min = 0, res = 0;
        for (int i = cur[u]; ~i && sum; i = e[i].nxt){
            cur[u] = i;
            int to = e[i].to;
            if (e[i].val && (depth[to] == depth[u] + 1)){
                Min = dfs(to, min(sum, e[i].val));
                if (Min == 0) depth[to] = -1; // 去掉增广完的点
                e[i].val -= Min;
                e[i ^ 1].val += Min;
                res += Min;
                sum -= Min;
            }
        }
        return res;
    }
    int dinic(){
        int ans = 0;
        while (bfs()){
            int k;
            while (k = dfs(s, INF)) ans += k;
        }
        return ans;
    }
    void Main(){
        memset(head, -1, sizeof(head));
        cin >> n >> m >> s >> t;
        while (m--){
            int u, v, w;
            cin >> u >> v >> w;
            add_Edge(u, v, w);
        }
        cout << dinic() << endl;
    }
};

时间复杂度：\(\operatorname{O}(n^2m)\)，同样实际上远低于
可以处理 \(10000-100000\) 的图