数值优化中 —— 置信域算法

DeepSeek 思考：

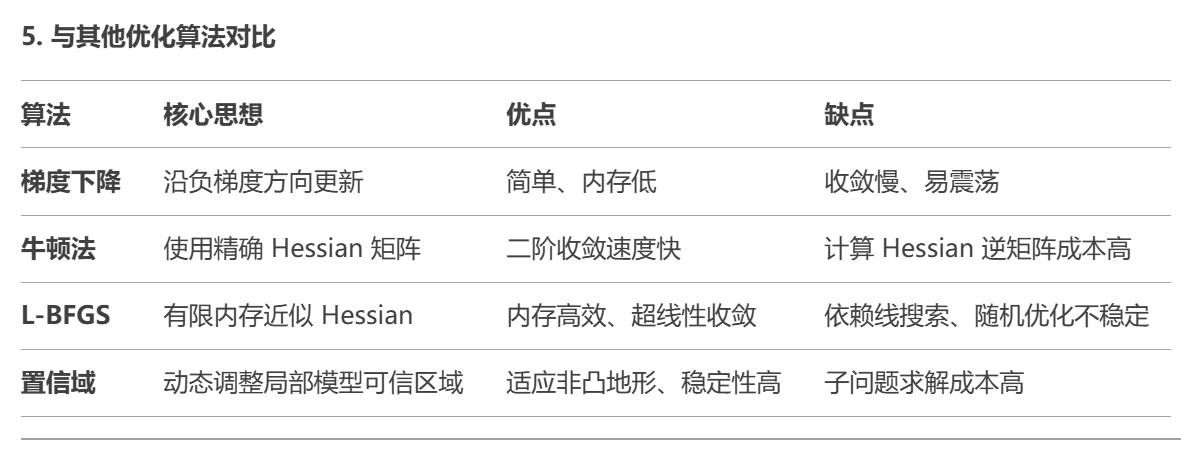
好的，我现在要详细理解数值优化中的置信域算法。首先，我需要明确什么是置信域算法，它和其他优化方法（比如梯度下降、牛顿法、L-BFGS）有什么不同。可能用户之前已经了解了L-BFGS，现在想扩展到置信域算法，所以需要对比它们的异同。

首先，我应该回忆一下优化问题的基本框架。优化问题通常是寻找一个函数的最小值，比如min f(x)。不同的优化方法有不同的策略，梯度下降是沿着负梯度方向更新，牛顿法利用二阶导数信息，L-BFGS则是近似Hessian矩阵来减少计算量。而置信域算法（Trust Region Method）则是另一种策略，它和线搜索方法不同，不是先确定方向再找步长，而是先确定一个区域，在这个区域内相信模型足够准确，然后在这个区域内寻找最优步长。

接下来，我需要理解置信域算法的基本思想。可能它的核心是在当前迭代点构造一个目标函数的近似模型，通常是二次模型，然后在这个模型的有效区域内（即置信域）寻找最优解。这个区域的半径会根据模型与实际函数的吻合程度进行调整。如果模型预测的很好，就扩大置信域；如果预测不好，就缩小。这样可以在保证模型精度的同时，有效控制步长。

然后，我需要了解置信域算法的具体步骤。大致应该包括：

1. 在当前点x_k，构建目标函数f的近似模型m_k(p)，通常是二次模型：m_k(p) = f(x_k) + ∇f(x_k)^T p + 0.5 p^T B_k p，其中B_k是Hessian或其近似，p是步长。

2. 确定一个置信域半径Δ_k，在这个区域内，模型m_k被信任能准确近似原函数f。

3. 在置信域内求解子问题，找到使得m_k(p)最小的p，即求解 min_p m_k(p) 满足 ||p|| ≤ Δ_k。

4. 计算实际下降量Δf = f(x_k) - f(x_k + p) 和预测下降量Δm = m_k(0) - m_k(p)。

5. 根据比值ρ=Δf/Δm来决定是否接受该步长，并调整置信域半径Δ_k：如果ρ接近1，说明模型准确，可以扩大半径；如果ρ很小甚至为负，则拒绝步长，缩小半径。

接着，我需要考虑置信域算法的关键点，比如如何构建模型，如何求解子问题，如何调整半径。例如，子问题是一个带约束的优化问题，可能需要用特定的方法求解，比如柯西点（Cauchy point）或者精确解。对于二次模型，可能使用共轭梯度法来求解，或者用其他数值方法。

然后，我需要举一个具体的例子来说明置信域算法的应用。例如，可以选一个简单的函数，如Rosenbrock函数，或者二次函数，展示算法每一步的过程。同时，可能需要比较置信域算法和其他方法在相同问题上的表现，比如收敛速度、稳定性等。

同时，用户可能希望了解置信域算法的优缺点。例如，优点包括在非凸问题中的稳定性，能够处理ill-conditioned问题，而缺点可能涉及计算子问题的复杂度，尤其是当维度很高时，求解带约束的子问题可能比较耗时。

此外，用户可能想知道置信域算法与其他方法的结合，比如在机器学习中的应用，或者如何与拟牛顿法（如L-BFGS）结合使用。比如，L-BFGS可以用来近似Hessian矩阵，而置信域方法用来控制步长，这样可能结合两者的优点。

在思考过程中，我需要注意可能存在的误区。比如，是否置信域算法一定比线搜索方法好？可能取决于具体问题。线搜索在确定方向后寻找合适的步长，而置信域是在一个区域内同时确定方向和步长，可能更适合某些情况，比如当模型在某个区域外不准确时。

另外，关于子问题的求解，我需要确认具体的解法。比如，对于置信域子问题，当使用二次模型时，可以通过求解一个带约束的优化问题来找到最优步长p。当约束是球形的（即||p|| ≤ Δ），可以用Moré-Sorensen算法，或者利用拉格朗日乘数法转化为一个无约束问题，通过调整λ来满足约束条件。这可能涉及到求解非线性方程，但具体的数值方法可能有不同的实现方式。

举例部分，可能需要具体数值的例子。例如，考虑一个简单的一维问题，比如最小化f(x)=x^4，初始点x0=2，置信域半径Δ=1。构建二次模型m(p)=f(x0) + f’(x0)p + 0.5 f''(x0)p²，这里可能Hessian是12x0²，即当前点的二阶导数。然后在这个区域内找到p，使得m(p)最小，并满足|p| ≤1。接着计算实际下降和预测下降的比率，调整半径。

但可能一维例子太简单，用户希望看到更实际的例子，比如二维的Rosenbrock函数，或者一个非线性最小二乘问题。例如，Rosenbrock函数f(x,y)=(a−x)^2 + b(y−x²⁾2，这是一个经典的测试函数，具有狭窄的谷底，适合测试优化算法。使用置信域方法，在迭代过程中调整半径，展示算法如何收敛到最小值点。

此外，用户可能希望了解置信域算法在实际中的应用，比如在深度学习中的使用。不过，可能置信域算法在大规模问题上由于子问题的计算成本较高，不如基于随机梯度的方法常用，但在某些情况下，如小批量或确定性优化中可能有应用。

最后，我需要确保解释清晰，逻辑连贯，涵盖算法原理、步骤、例子、优缺点，以及与其他方法的对比。同时，例子要具体，可能包括数学推导或伪代码，帮助读者理解实现过程。

在总结时，需要指出置信域算法是一种强大的优化方法，尤其适用于模型近似精度变化较大的情况，通过动态调整信任区域来平衡全局探索和局部开发，适用于中小规模的优化问题，可能在大规模问题上需要结合其他技术以降低计算复杂度。

7. 代码示例（Python 伪代码）

import numpy as np

def trust_region(f, grad, hessian_approx, x0, max_iter=100, delta0=1.0, eta=0.1):
    x = x0
    delta = delta0
    for _ in range(max_iter):
        g = grad(x)
        B = hessian_approx(x)  # 例如 BFGS 近似
        p = solve_subproblem(g, B, delta)  # 求解子问题（如 Dogleg 方法）
        actual_reduction = f(x) - f(x + p)
        predicted_reduction = - (g.T @ p + 0.5 * p.T @ B @ p)
        rho = actual_reduction / predicted_reduction
        
        if rho < 0.25:
            delta *= 0.5
        elif rho > 0.75 and np.linalg.norm(p) == delta:
            delta *= 2.0
        
        if rho > eta:
            x = x + p
    return x

# 示例：使用 Dogleg 方法求解子问题
def solve_subproblem(g, B, delta):
    p_u = - (g.T @ g) / (g.T @ B @ g) * g  # 最速下降方向
    p_b = -np.linalg.solve(B, g)           # 牛顿方向
    if np.linalg.norm(p_b) <= delta:
        return p_b
    elif np.linalg.norm(p_u) >= delta:
        return (delta / np.linalg.norm(p_u)) * p_u
    else:
        # 计算 Dogleg 路径交点
        t = find_intersection(p_u, p_b - p_u, delta)
        return p_u + t * (p_b - p_u)