强化学习算法中的log_det_jacobian —— 概率分布的仿射变换（Bijector）（续）

前文：

强化学习算法中的log_det_jacobian —— 概率分布的仿射变换（Bijector）

前文说到概率分布的仿射变换（Bijector）在贝叶斯、变分推断等领域有很重要的作用，但是在强化学习中呢，其实在强化学习中也会用到，但是最为普遍的应用场景其实只是做简单的tanh变换。

在强化学习中一般用高斯分布来表示连续动作的策略，但是在很多应用环境中，如：人形机器人领域，连续动作的空间不是[-Inf, Inf]，而是[-1, +1]，这时则需要进行tanh变换，具体为：

X ~ Normal(loc, scale)
Y = tanh(X)
action = Y

可以看到，这是一种比较简单的概率分布的仿射变换（Bijector），如果按照前文给出的概率变换公式，我们可以得到action，即y的概率：

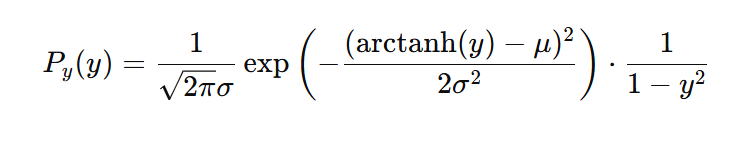
也就是说，当：

X ~ Normal(loc, scale)
Y = tanh(X)
action = Y

有：
P(Y=y)=P(X=arctanh(y))*(arctanh(y))'

= P(X=arctanh(y))*\((1 - y^2)^{-1}\)

所以:

log_P(Y=y)

= log_P(X=arctanh(y)) + log_(arctanh(y))'

= log_P(X=arctanh(y)) - log_(\(1-y^2\))

= log_P(X=x) - log_(1 - \(tanh^2(x)\))

补充；

log_det_jacobian = 2 * (math.log(2) - dist - F.softplus(-2 * dist))
= log( tanh'(x) )
= \(log( 1 - ( tanh(x) )\\^2 )\)

上面的推导的重点结论：

\(Y=tanh(X)\)

\(logP(Y=y)=logP(X=x)-log(1-tanh^2(x))\)

所以，在强化学习的policy输出的概率X服从高斯分布，最终输入给环境的是Y=tanh(X)，而进行loss函数计算时使用的logP(Y=y)可以通过\(logP(X=x)-log(1-tanh^2(x))\)来获得，而我们在使用强化学习策略进行采样时我们记录的action为X，而不需要记录Y，这样在进行最终的loss函数计算时x=action，也就是x为采样时的抽样动作action，如果使用代码形式，则有：

log_det_jacobian = 2 * (math.log(2) - dist - F.softplus(-2 * dist))

在强化学习算法中的具体使用可以参考PPO项目代码实现，地址：

https://colab.research.google.com/github/google/brax/blob/main/notebooks/training_torch.ipynb

具体：

  @torch.jit.export
  def dist_log_prob(self, loc, scale, dist):
    log_unnormalized = -0.5 * ((dist - loc) / scale).square()
    log_normalized = 0.5 * math.log(2 * math.pi) + torch.log(scale)
    log_det_jacobian = 2 * (math.log(2) - dist - F.softplus(-2 * dist))
    log_prob = log_unnormalized - log_normalized - log_det_jacobian
    return log_prob.sum(dim=-1)

不过该种方法计算概率随着分布变换的改变还是比较容易实现和好理解的，但是对于信息熵的计算就不是很直观了。

由于动作空间是连续的，也就是说X的取值范围为[-Inf， +Inf]，而Y的取值范围为[-1, +1]，而信息熵并不只是单纯的进行概率计算，而是需要对概率进行积分计算。

通过之前的文章的分析和上面的推导，我们获得了重要的公式，即：

$ Y = tanh(X) $

$ x = arctanh(y) $

\(logP(Y=y)=logP(X=x)-log(1-tanh^2(x))\)

那么我们可以得到：

Entroy(Y=y)

\(=-\int_{-1}^{1} P(Y=y)log P(Y=y)dy\)

\(= - \int_{-\infty}^{\infty} P(X=x) * (1-tanh^{2}(x))^{-1} * (log P(X=x)-log(1-tanh^{2}(x))) * (1 - tanh^{2}(x))dx\)

\(= - \int_{-\infty}^{\infty} P(X=x) * ( log P(X=x)-log(1-tanh^{2}(x)) ) dx\)

\(= - \int_{-\infty}^{\infty} P(X=x) * log P(X=x)+\int_{-\infty}^{\infty} P(X=x) log(1-tanh^{2}(x)) dx\)

\(=Entroy(X=x) + \int_{-\infty}^{\infty} P(X=x) log(1-tanh^{2}(x)) dx\)

y是x通过tanh变换获得的，x是服从高斯分布的，因此Entroy(X=x)是可以通过公式获得的，但是对于复杂积分我们是无法通过公式进行快速获得的，对于这样的问题我们只有通过采样的方法获得近似的积分值，因此对于\(\int_{-\infty}^{\infty} P(X=x) log(1-tanh^{2}(x)) dx\)我们是无法通过公式进行直接计算的。

在https://colab.research.google.com/github/google/brax/blob/main/notebooks/training_torch.ipynb中对\(\int_{-\infty}^{\infty} P(X=x) log(1-tanh^{2}(x)) dx\)给出了近似的解决方法，代码如下：

  @torch.jit.export
  def dist_entropy(self, loc, scale):
    log_normalized = 0.5 * math.log(2 * math.pi) + torch.log(scale)
    entropy = 0.5 + log_normalized
    entropy = entropy * torch.ones_like(loc)
    dist = torch.normal(loc, scale)
    log_det_jacobian = 2 * (math.log(2) - dist - F.softplus(-2 * dist))
    entropy = entropy + log_det_jacobian
    return entropy.sum(dim=-1)

通过上面代码中的：

    dist = torch.normal(loc, scale)
    log_det_jacobian = 2 * (math.log(2) - dist - F.softplus(-2 * dist))

可以知道，上面实现中其实是只做了一次的抽样计算其log_det_jacobian，也就是\(log(1-tanh^{2}(x))\)，可以看到在上面的实现中其实也没有做积分，也就是没有求期望，我们可以认为\(log(1-tanh^{2}(x))\)是\(\int_{-\infty}^{\infty} P(X=x) log(1-tanh^{2}(x)) dx\)的一次抽样，也可以看做是一种近似，如果需要获得更准确的分布变换后的修正，那么我们就需要进行蒙特卡洛这样的大规模采样，然后通过计算其离散积分从而获得对连续积分的更准确的近似，但是这样的计算方法是不现实的，因为如果在这种的修正项上花费这么大的计算量是与我们的求解主题不符的，这并不是主线任务，由于上面的代码是Google官方的实现代码，可以看做这种对分布变换后信息熵的近似修正是一种被业界认可和采样的方法。

高斯函数的信息熵求解公式：