如何理解最优化问题中的“牛顿法” —— 牛顿法求解最优值

计算机学科中的数值优化问题中的最经典的算法估计是“牛顿法”，虽然接触这个最经典的数值优化算法好多年了，但是总不是很理解，最近再次遇到这个算法，于是记录下自己的一些理解。

参考：

最优化--梯度下降法--牛顿法（详解）

【最优化(四)】无约束优化问题的牛顿法及其代码实现

---

优化目标函数为 f(x)，求最小值。

假设现在的x值为\(x_k\)
我们需要得到一个新的x值，即 \(x_k+d_k\) 以保证 \(f(x_k+d_k)\\<f(x_k)\)

虽然我们的最终目标是求得最小的f(x)，但是在一步的优化中我们只需要求得x值为\(x_k\)时的最小\(f(x_k+d_k)\)，也就是求这个一步优化中从x值为\(x_k\)处出发的使f(x)最小的向量\(d_k\)

我们可以将\(f(x_k+d_k)\)进行泰勒级数展开，得到：

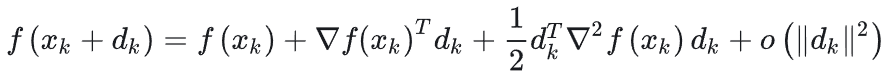
我们可以把上式中右半部分看做是关于向量\(d_k\)的一个函数，也就是求关于向量\(d_k\)的最小\(f(x_k+d_k)\)可以写为关于向量\(d_k\)的函数：

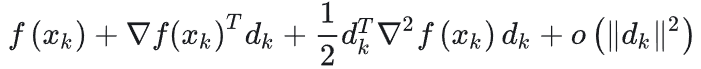
因为这个式子是关于变量\(d_k\)的，因此对这个式子求对于变量\(d_k\)的导数，当其导数为零时这个式子取极小值，于是有下面的式子：（忽略上式中的极小项）

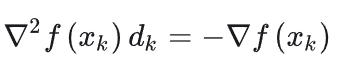
上式又被叫做牛顿方程，假设上式中二阶导项可逆，并且上式为关于变量\(d_k\)的，由此可以得到：

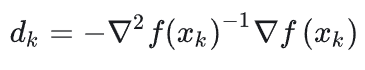
这样我们就求得了当x为\(x_k\)时一步优化获得的最小x值，即\(x_k+1=x_k+d_k\)

如此迭代计算，保证每一步优化过程中均可保证\(f(x_k+d_k)\\<f(x_k)\)，以此获得最终的最小f(x)值，实现优化目标，该过程就是数值优化方法中的经典“牛顿法”。

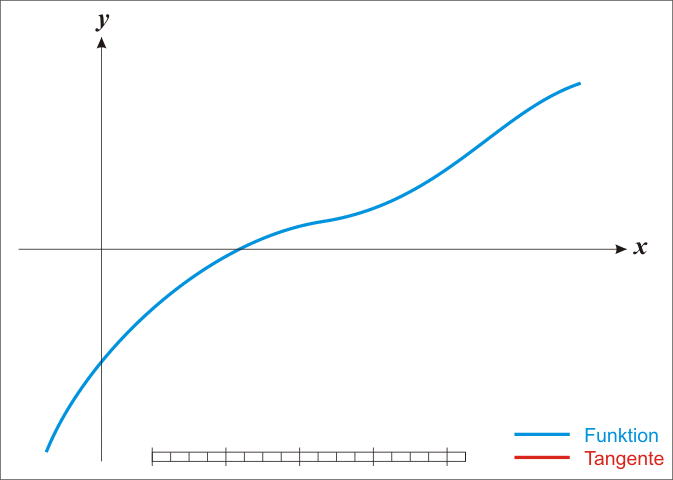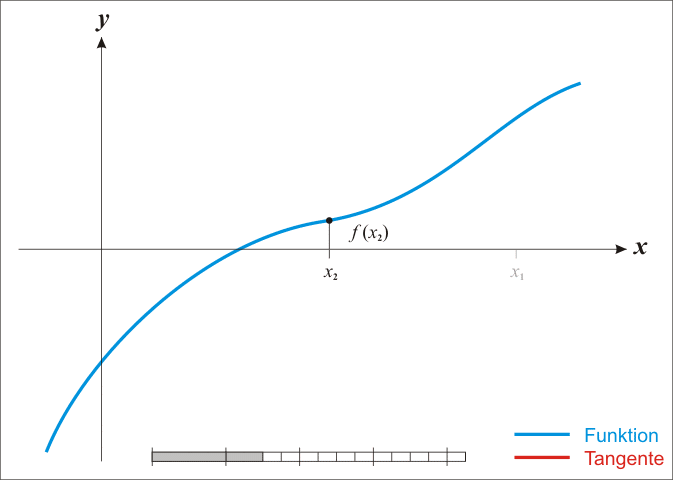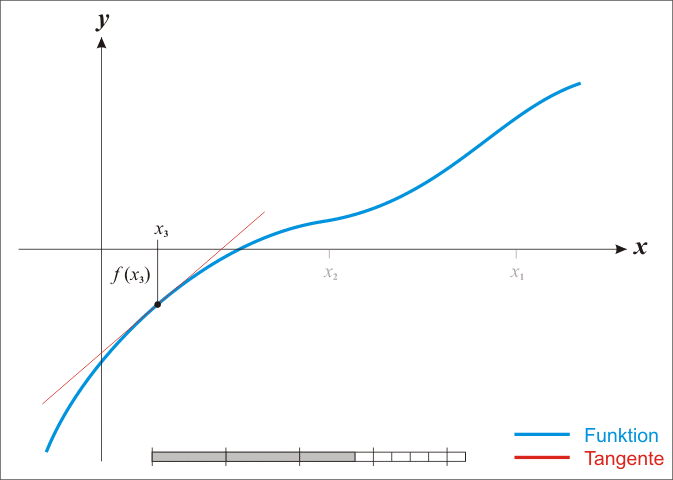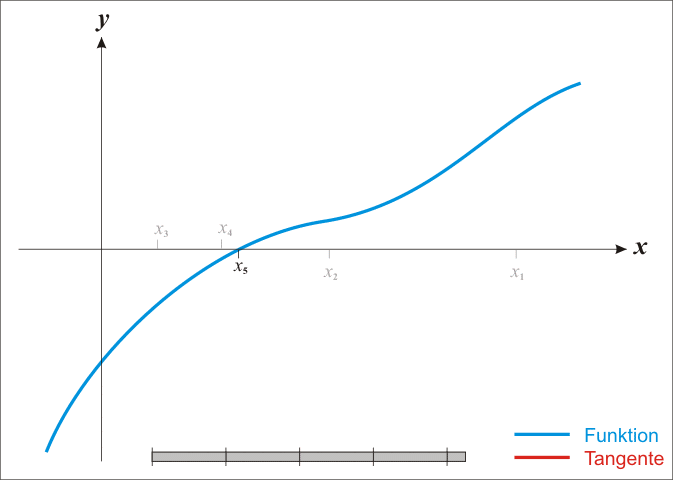
给出 https://blog.csdn.net/m0_67093160/article/details/131452860 中的一个示意图：