凸优化： 回溯线搜索（Backtracking line search）

声明：

本文大量摘录 https://www.cnblogs.com/kemaswill/p/3416231.html 内容。

 

 

======================================

 

 

回溯线搜索（Backtracking line search）

 

预备知识：

函数的梯度--最快上升方向。下降方向则是负梯度。

 

 

给出 回溯线搜索（Backtracking line search）的算法流程描述：

 

 

 

 

 ===================================================

 

 

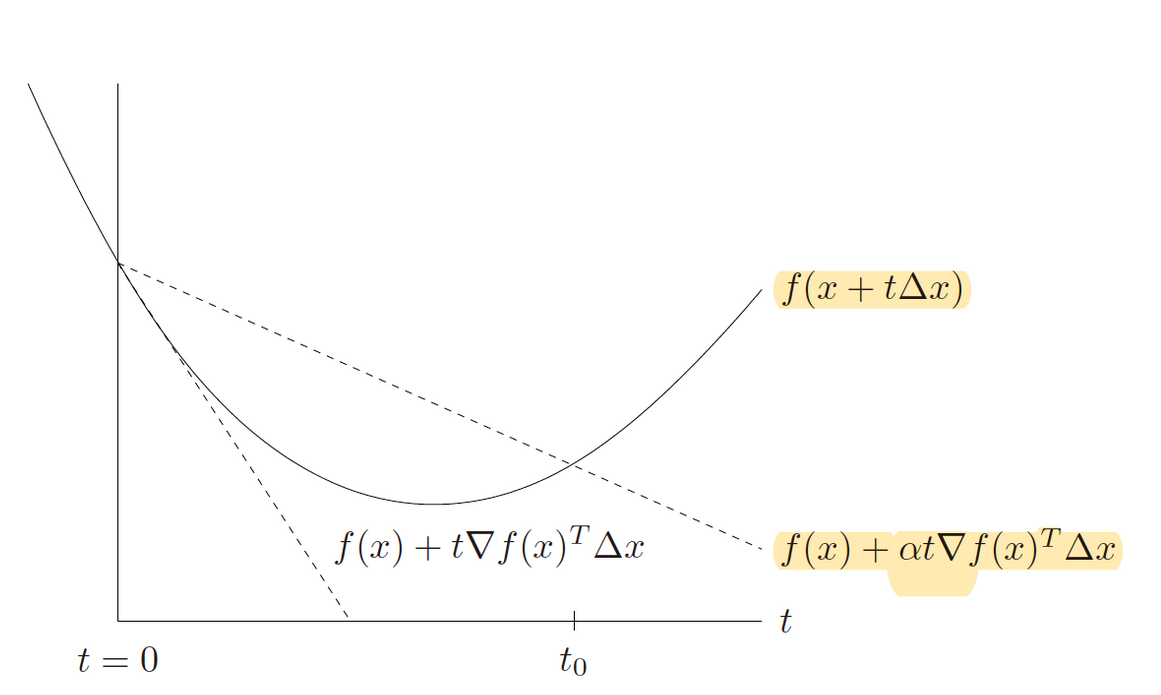
下面内容摘录自：

https://www.cnblogs.com/kemaswill/p/3416231.html

个人推荐阅读上面这个链接的内容，这个内容比较易懂，而且讲的也比较透彻。

 

 

 

 

 

===================================================

 

 

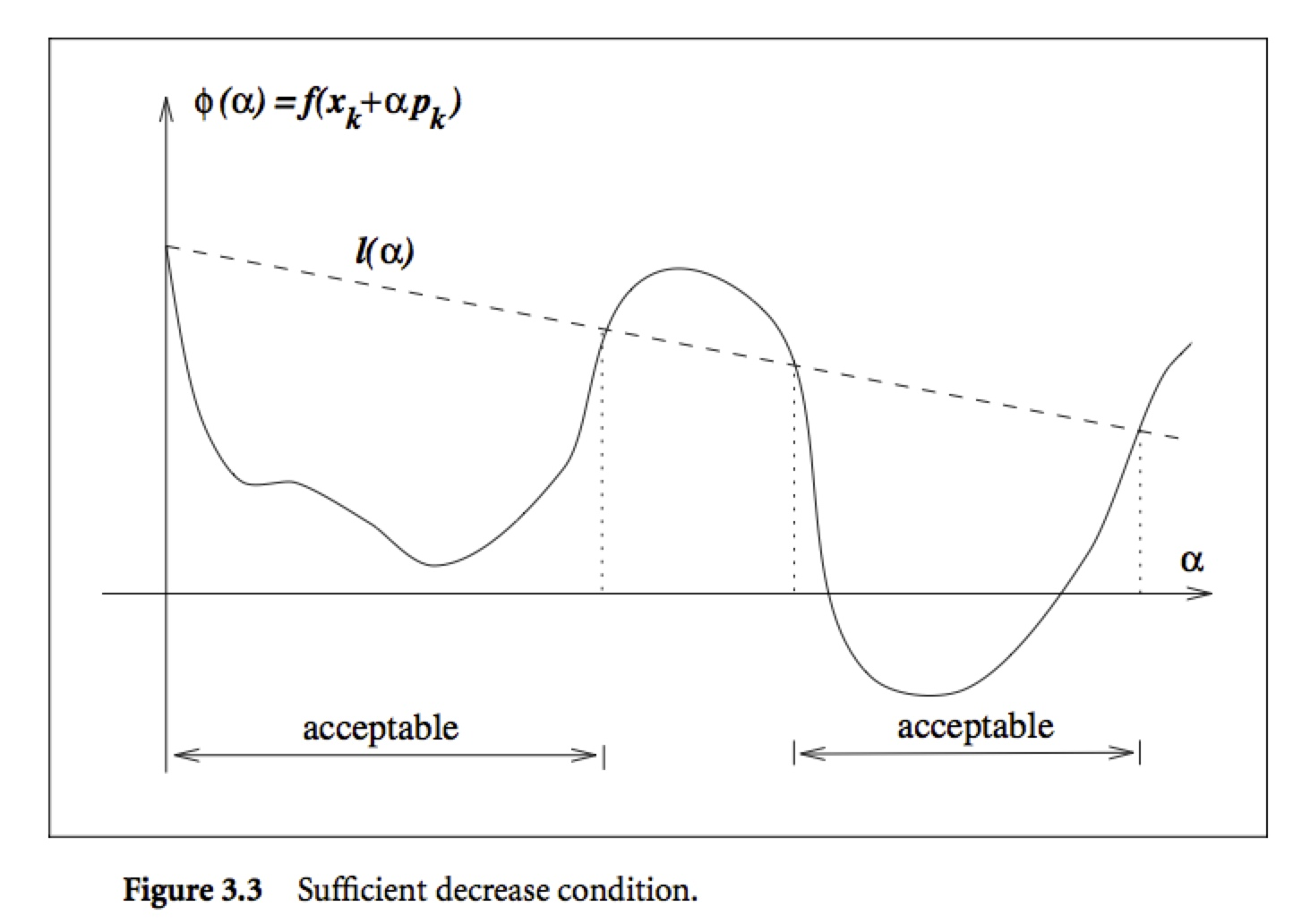
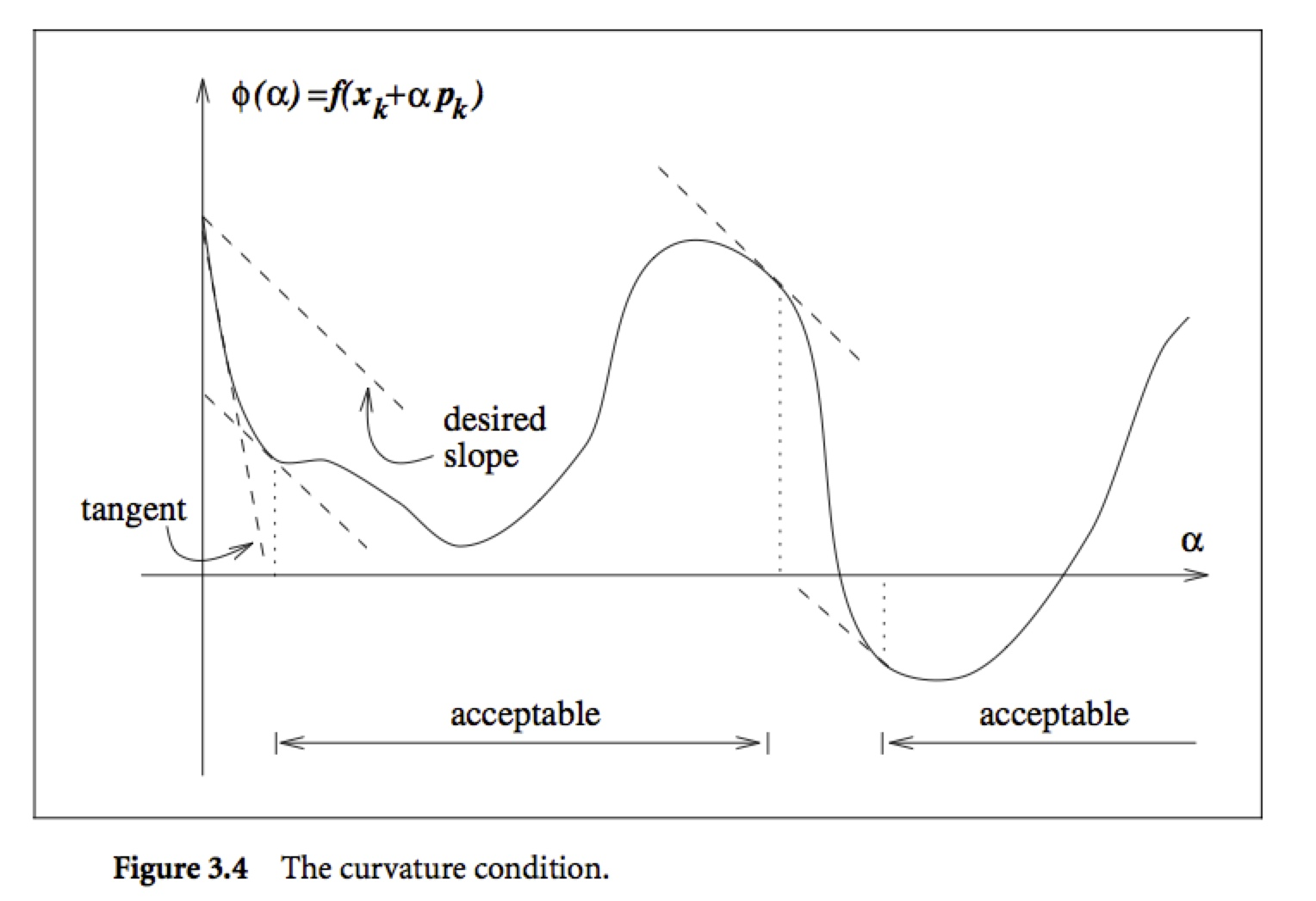
根据 https://www.cnblogs.com/kemaswill/p/3416231.html 中的理论，我们可以得到下面的demo代码：

import random
import numpy as np
from scipy.linalg import orth
import torch

seed = 9999
random.seed(seed)
np.random.seed(seed)

torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True


class Data_Gen():
    def __init__(self, N, positive_definite=True):
        self.N = N

        # 不变的矩阵
        B = np.random.rand(N, 1)
        # 数据集，数据B矩阵
        self.B = torch.tensor(B, dtype=torch.float32)

        if positive_definite==True:
            # 正定矩阵的生成, A_
            X = np.diag(np.abs(np.random.rand(N))+1)
            U = orth(np.random.rand(N, N))
            A = np.dot(np.dot(U.T, X), U)
        else:
            # 非正定矩阵的生成，A
            M = np.random.rand(N, N)
            A = np.dot(M.T, M) + 0.01*np.eye(N)
        self.A = torch.tensor(A, dtype=torch.float32)

    def data_gen(self, x: torch.FloatTensor):
        """ 数据生成 """
        # 训练数据，x_data, x
        # x = torch.randn(N, requires_grad=True)
        N = x.size()[0]
        assert N==self.N, "向量长度不匹配"

        # 构建训练数据，非正定数据矩阵生成的y_data
        y=self.object_fun(self.A, self.B, x)
        return y

    def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
        if x.dim() == 1:
            x = torch.unsqueeze(x, 1)
        ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
        # print( torch.mm(A, x) )
        # print( torch.mm(x.T, torch.mm(A, x)) )
        # print( torch.mm(x.T, B) )
        return torch.squeeze(ans)


#####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
    # x = torch.randn(N, device="cuda:0", requires_grad=True)
    y = data_gen.data_gen(x)

    iter_num = 0
    while True:
        g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
        x.data.add_( -step*g )
        y_new = data_gen.data_gen(x)

        iter_num += 1
        print("iter_num: ", iter_num, "y_old: ", y.item(),  "y_new: ", y_new.item())
        if abs(y_new.item()-y.item()) < 0.00001:
            break
        else:
            y = y_new


#####################################################
#  回溯线搜索（Backtracking line search）
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
    iter_num = 0
    c = 0.25
    beta = 0.8
    while True:
        iter_num += 1
        y0 = data_gen.data_gen(x) 
        g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0]
        
        p = -1.0*g  # 求最小值，梯度下降，使用负梯度
        delta_f = g

        search_time = 0
        alpha_step = 1.0
        while True:
            y_new = data_gen.data_gen(x.detach() + alpha_step*p) 
            y_up = y0 + c*alpha_step*torch.dot(delta_f, p)

            if y_new.item() > y_up.item():
                search_time += 1
                alpha_step *= beta
            else:
                break
        x.data.add_( alpha_step*p )

        print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
        if abs(y_new.item()-y0.item()) < 0.00001:
            break


if __name__ == '__main__':
    # 数据生成
    N = 500
    data_gen = Data_Gen(N)
    x = torch.randn(N, requires_grad=True)

    #####################################################
    # 对凸二次函数进行求解，正定矩阵，求解最小值
    #####################################################
    # data_gen = Data_Gen(N)

    # 随机梯度法
    sgd(x, data_gen)

    # bls算法
    bls(x, data_gen)


    #####################################################
    # 对非凸二次函数进行求解，非正定矩阵，求解最小值
    #####################################################
    """
    data_gen = Data_Gen(N, positive_definite=False)

    # 随机梯度法
    sgd(x, data_gen)

    # bls算法
    bls(x, data_gen)
    """

 

 

对于二阶正定矩阵所形成的凸优化问题，我们使用随机梯度下降，代码：

import random
import numpy as np
from scipy.linalg import orth
import torch

seed = 9999
random.seed(seed)
np.random.seed(seed)

torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True


class Data_Gen():
    def __init__(self, N, positive_definite=True):
        self.N = N

        # 不变的矩阵
        B = np.random.rand(N, 1)
        # 数据集，数据B矩阵
        self.B = torch.tensor(B, dtype=torch.float32)

        if positive_definite==True:
            # 正定矩阵的生成, A_
            X = np.diag(np.abs(np.random.rand(N))+1)
            U = orth(np.random.rand(N, N))
            A = np.dot(np.dot(U.T, X), U)
        else:
            # 非正定矩阵的生成，A
            M = np.random.rand(N, N)
            A = np.dot(M.T, M) + 0.01*np.eye(N)
        self.A = torch.tensor(A, dtype=torch.float32)

    def data_gen(self, x: torch.FloatTensor):
        """ 数据生成 """
        # 训练数据，x_data, x
        # x = torch.randn(N, requires_grad=True)
        N = x.size()[0]
        assert N==self.N, "向量长度不匹配"

        # 构建训练数据，非正定数据矩阵生成的y_data
        y=self.object_fun(self.A, self.B, x)
        return y

    def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
        if x.dim() == 1:
            x = torch.unsqueeze(x, 1)
        ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
        # print( torch.mm(A, x) )
        # print( torch.mm(x.T, torch.mm(A, x)) )
        # print( torch.mm(x.T, B) )
        return torch.squeeze(ans)


#####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
    # x = torch.randn(N, device="cuda:0", requires_grad=True)
    y = data_gen.data_gen(x)

    iter_num = 0
    while True:
        g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
        x.data.add_( -step*g )
        y_new = data_gen.data_gen(x)

        iter_num += 1
        print("iter_num: ", iter_num, "y_old: ", y.item(),  "y_new: ", y_new.item())
        if abs(y_new.item()-y.item()) < 0.00001:
            break
        else:
            y = y_new


#####################################################
#  回溯线搜索（Backtracking line search）
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
    iter_num = 0
    c = 0.25
    beta = 0.8
    while True:
        iter_num += 1
        y0 = data_gen.data_gen(x) 
        g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0]
        
        p = -1.0*g  # 求最小值，梯度下降，使用负梯度
        delta_f = g

        search_time = 0
        alpha_step = 1.0
        while True:
            y_new = data_gen.data_gen(x.detach() + alpha_step*p) 
            y_up = y0 + c*alpha_step*torch.dot(delta_f, p)

            if y_new.item() > y_up.item():
                search_time += 1
                alpha_step *= beta
            else:
                break
        x.data.add_( alpha_step*p )

        print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
        if abs(y_new.item()-y0.item()) < 0.00001:
            break


if __name__ == '__main__':
    # 数据生成
    N = 500
    data_gen = Data_Gen(N)
    x = torch.randn(N, requires_grad=True)

    #####################################################
    # 对凸二次函数进行求解，正定矩阵，求解最小值
    #####################################################
    # data_gen = Data_Gen(N)

    # 随机梯度法
    sgd(x, data_gen)

    # bls算法
    # bls(x, data_gen)


    #####################################################
    # 对非凸二次函数进行求解，非正定矩阵，求解最小值
    #####################################################
    """
    data_gen = Data_Gen(N, positive_definite=False)

    # 随机梯度法
    sgd(x, data_gen)

    # bls算法
    bls(x, data_gen)
    """

运行结果：

iter_num:  109598 y_old:  -24.1126766204834 y_new:  -24.11280059814453
iter_num:  109599 y_old:  -24.11280059814453 y_new:  -24.11285972595215
iter_num:  109600 y_old:  -24.11285972595215 y_new:  -24.112972259521484
iter_num:  109601 y_old:  -24.112972259521484 y_new:  -24.113067626953125
iter_num:  109602 y_old:  -24.113067626953125 y_new:  -24.113168716430664
iter_num:  109603 y_old:  -24.113168716430664 y_new:  -24.113237380981445
iter_num:  109604 y_old:  -24.113237380981445 y_new:  -24.11332130432129
iter_num:  109605 y_old:  -24.11332130432129 y_new:  -24.113388061523438
iter_num:  109606 y_old:  -24.113388061523438 y_new:  -24.11349868774414
iter_num:  109607 y_old:  -24.11349868774414 y_new:  -24.11361312866211
iter_num:  109608 y_old:  -24.11361312866211 y_new:  -24.113622665405273

对于二阶正定矩阵所形成的凸优化问题，我们使用bls算法，代码：

import random
import numpy as np
from scipy.linalg import orth
import torch

seed = 9999
random.seed(seed)
np.random.seed(seed)

torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True


class Data_Gen():
    def __init__(self, N, positive_definite=True):
        self.N = N

        # 不变的矩阵
        B = np.random.rand(N, 1)
        # 数据集，数据B矩阵
        self.B = torch.tensor(B, dtype=torch.float32)

        if positive_definite==True:
            # 正定矩阵的生成, A_
            X = np.diag(np.abs(np.random.rand(N))+1)
            U = orth(np.random.rand(N, N))
            A = np.dot(np.dot(U.T, X), U)
        else:
            # 非正定矩阵的生成，A
            M = np.random.rand(N, N)
            A = np.dot(M.T, M) + 0.01*np.eye(N)
        self.A = torch.tensor(A, dtype=torch.float32)

    def data_gen(self, x: torch.FloatTensor):
        """ 数据生成 """
        # 训练数据，x_data, x
        # x = torch.randn(N, requires_grad=True)
        N = x.size()[0]
        assert N==self.N, "向量长度不匹配"

        # 构建训练数据，非正定数据矩阵生成的y_data
        y=self.object_fun(self.A, self.B, x)
        return y

    def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
        if x.dim() == 1:
            x = torch.unsqueeze(x, 1)
        ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
        # print( torch.mm(A, x) )
        # print( torch.mm(x.T, torch.mm(A, x)) )
        # print( torch.mm(x.T, B) )
        return torch.squeeze(ans)


#####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
    # x = torch.randn(N, device="cuda:0", requires_grad=True)
    y = data_gen.data_gen(x)

    iter_num = 0
    while True:
        g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
        x.data.add_( -step*g )
        y_new = data_gen.data_gen(x)

        iter_num += 1
        print("iter_num: ", iter_num, "y_old: ", y.item(),  "y_new: ", y_new.item())
        if abs(y_new.item()-y.item()) < 0.00001:
            break
        else:
            y = y_new


#####################################################
#  回溯线搜索（Backtracking line search）
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
    iter_num = 0
    c = 0.25
    beta = 0.8
    while True:
        iter_num += 1
        y0 = data_gen.data_gen(x) 
        g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0]
        
        p = -1.0*g  # 求最小值，梯度下降，使用负梯度
        delta_f = g

        search_time = 0
        alpha_step = 1.0
        while True:
            y_new = data_gen.data_gen(x.detach() + alpha_step*p) 
            y_up = y0 + c*alpha_step*torch.dot(delta_f, p)

            if y_new.item() > y_up.item():
                search_time += 1
                alpha_step *= beta
            else:
                break
        x.data.add_( alpha_step*p )

        print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
        if abs(y_new.item()-y0.item()) < 0.00001:
            break


if __name__ == '__main__':
    # 数据生成
    N = 500
    data_gen = Data_Gen(N)
    x = torch.randn(N, requires_grad=True)

    #####################################################
    # 对凸二次函数进行求解，正定矩阵，求解最小值
    #####################################################
    # data_gen = Data_Gen(N)

    # 随机梯度法
    # sgd(x, data_gen)

    # bls算法
    bls(x, data_gen)


    #####################################################
    # 对非凸二次函数进行求解，非正定矩阵，求解最小值
    #####################################################
    """
    data_gen = Data_Gen(N, positive_definite=False)

    # 随机梯度法
    sgd(x, data_gen)

    # bls算法
    bls(x, data_gen)
    """

运行结果：

iter_num:  1 search_time:  4  y_old:  741.302490234375 y_new:  61.191226959228516
iter_num:  2 search_time:  4  y_old:  61.191226959228516 y_new:  -6.580791473388672
iter_num:  3 search_time:  5  y_old:  -6.580791473388672 y_new:  -24.848424911499023
iter_num:  4 search_time:  5  y_old:  -24.848424911499023 y_new:  -25.728652954101562
iter_num:  5 search_time:  5  y_old:  -25.728652954101562 y_new:  -25.78291893005371
iter_num:  6 search_time:  5  y_old:  -25.78291893005371 y_new:  -25.786640167236328
iter_num:  7 search_time:  5  y_old:  -25.786640167236328 y_new:  -25.786869049072266
iter_num:  8 search_time:  3  y_old:  -25.786869049072266 y_new:  -25.786916732788086
iter_num:  9 search_time:  5  y_old:  -25.786916732788086 y_new:  -25.786951065063477
iter_num:  10 search_time:  3  y_old:  -25.786951065063477 y_new:  -25.78696060180664

可以看到，对于凸优化问题，我们使用随机梯度下降和bls算法相差不大，甚至bls算法的结果要由于随机梯度下降，但是最为重要的是运算的迭代次数，我们可以看到随机梯度下降算法共进行了109608次迭代，而bls算法只进行了10次迭代，虽然bls算法在每次迭代的过程中都会进行search操作，但是每次迭代过程中search次数都没有超过5。

可以看到对于凸优化问题，bls算法在总体表现上要优与随机梯度sgd算法。

 

 

 

 

对于非凸优化问题，给出demo代码：

非凸优化问题，随机梯度下降算法，sgd:

import random
import numpy as np
from scipy.linalg import orth
import torch

seed = 9999
random.seed(seed)
np.random.seed(seed)

torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True


class Data_Gen():
    def __init__(self, N, positive_definite=True):
        self.N = N

        # 不变的矩阵
        B = np.random.rand(N, 1)
        # 数据集，数据B矩阵
        self.B = torch.tensor(B, dtype=torch.float32)

        if positive_definite==True:
            # 正定矩阵的生成, A_
            X = np.diag(np.abs(np.random.rand(N))+1)
            U = orth(np.random.rand(N, N))
            A = np.dot(np.dot(U.T, X), U)
        else:
            # 非正定矩阵的生成，A
            M = np.random.rand(N, N)
            A = np.dot(M.T, M) + 0.01*np.eye(N)
        self.A = torch.tensor(A, dtype=torch.float32)

    def data_gen(self, x: torch.FloatTensor):
        """ 数据生成 """
        # 训练数据，x_data, x
        # x = torch.randn(N, requires_grad=True)
        N = x.size()[0]
        assert N==self.N, "向量长度不匹配"

        # 构建训练数据，非正定数据矩阵生成的y_data
        y=self.object_fun(self.A, self.B, x)
        return y

    def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
        if x.dim() == 1:
            x = torch.unsqueeze(x, 1)
        ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
        # print( torch.mm(A, x) )
        # print( torch.mm(x.T, torch.mm(A, x)) )
        # print( torch.mm(x.T, B) )
        return torch.squeeze(ans)


#####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
    # x = torch.randn(N, device="cuda:0", requires_grad=True)
    y = data_gen.data_gen(x)

    iter_num = 0
    while True:
        g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
        x.data.add_( -step*g )
        y_new = data_gen.data_gen(x)

        iter_num += 1
        print("iter_num: ", iter_num, "y_old: ", y.item(),  "y_new: ", y_new.item())
        if abs(y_new.item()-y.item()) < 0.00001:
            break
        else:
            y = y_new


#####################################################
#  回溯线搜索（Backtracking line search）
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
    iter_num = 0
    c = 0.25
    beta = 0.8
    while True:
        iter_num += 1
        y0 = data_gen.data_gen(x) 
        g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0]
        
        p = -1.0*g  # 求最小值，梯度下降，使用负梯度
        delta_f = g

        search_time = 0
        alpha_step = 1.0
        while True:
            y_new = data_gen.data_gen(x.detach() + alpha_step*p) 
            y_up = y0 + c*alpha_step*torch.dot(delta_f, p)

            if y_new.item() > y_up.item():
                search_time += 1
                alpha_step *= beta
            else:
                break
        x.data.add_( alpha_step*p )

        print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
        if abs(y_new.item()-y0.item()) < 0.00001:
            break


if __name__ == '__main__':
    # 数据生成
    N = 500
    x = torch.randn(N, requires_grad=True)

    """
    #####################################################
    # 对凸二次函数进行求解，正定矩阵，求解最小值
    #####################################################
    # data_gen = Data_Gen(N)

    # 随机梯度法
    # sgd(x, data_gen)

    # bls算法
    bls(x, data_gen)
    """

    #####################################################
    # 对非凸二次函数进行求解，非正定矩阵，求解最小值
    #####################################################
    data_gen = Data_Gen(N, positive_definite=False)

    # 随机梯度法
    sgd(x, data_gen)

    # bls算法
    # bls(x, data_gen)

运算结果：

iter_num:  18261 y_old:  29.948509216308594 y_new:  29.945993423461914
iter_num:  18262 y_old:  29.945993423461914 y_new:  29.94289207458496
iter_num:  18263 y_old:  29.94289207458496 y_new:  29.940031051635742
iter_num:  18264 y_old:  29.940031051635742 y_new:  29.93958282470703
iter_num:  18265 y_old:  29.93958282470703 y_new:  29.936599731445312
iter_num:  18266 y_old:  29.936599731445312 y_new:  29.932973861694336
iter_num:  18267 y_old:  29.932973861694336 y_new:  29.930309295654297
iter_num:  18268 y_old:  29.930309295654297 y_new:  29.92643165588379
iter_num:  18269 y_old:  29.92643165588379 y_new:  29.92643928527832

 

非凸优化问题，bls算法，代码：

 

import random
import numpy as np
from scipy.linalg import orth
import torch

seed = 9999
random.seed(seed)
np.random.seed(seed)

torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True


class Data_Gen():
    def __init__(self, N, positive_definite=True):
        self.N = N

        # 不变的矩阵
        B = np.random.rand(N, 1)
        # 数据集，数据B矩阵
        self.B = torch.tensor(B, dtype=torch.float32)

        if positive_definite==True:
            # 正定矩阵的生成, A_
            X = np.diag(np.abs(np.random.rand(N))+1)
            U = orth(np.random.rand(N, N))
            A = np.dot(np.dot(U.T, X), U)
        else:
            # 非正定矩阵的生成，A
            M = np.random.rand(N, N)
            A = np.dot(M.T, M) + 0.01*np.eye(N)
        self.A = torch.tensor(A, dtype=torch.float32)

    def data_gen(self, x: torch.FloatTensor):
        """ 数据生成 """
        # 训练数据，x_data, x
        # x = torch.randn(N, requires_grad=True)
        N = x.size()[0]
        assert N==self.N, "向量长度不匹配"

        # 构建训练数据，非正定数据矩阵生成的y_data
        y=self.object_fun(self.A, self.B, x)
        return y

    def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
        if x.dim() == 1:
            x = torch.unsqueeze(x, 1)
        ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
        # print( torch.mm(A, x) )
        # print( torch.mm(x.T, torch.mm(A, x)) )
        # print( torch.mm(x.T, B) )
        return torch.squeeze(ans)


#####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
    # x = torch.randn(N, device="cuda:0", requires_grad=True)
    y = data_gen.data_gen(x)

    iter_num = 0
    while True:
        g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
        x.data.add_( -step*g )
        y_new = data_gen.data_gen(x)

        iter_num += 1
        print("iter_num: ", iter_num, "y_old: ", y.item(),  "y_new: ", y_new.item())
        if abs(y_new.item()-y.item()) < 0.00001:
            break
        else:
            y = y_new


#####################################################
#  回溯线搜索（Backtracking line search）
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
    iter_num = 0
    c = 0.25
    beta = 0.8
    while True:
        iter_num += 1
        y0 = data_gen.data_gen(x) 
        g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0]
        
        p = -1.0*g  # 求最小值，梯度下降，使用负梯度
        delta_f = g

        search_time = 0
        alpha_step = 1.0
        while True:
            y_new = data_gen.data_gen(x.detach() + alpha_step*p) 
            y_up = y0 + c*alpha_step*torch.dot(delta_f, p)

            if y_new.item() > y_up.item():
                search_time += 1
                alpha_step *= beta
            else:
                break
        x.data.add_( alpha_step*p )

        print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
        if abs(y_new.item()-y0.item()) < 0.00001:
            break


if __name__ == '__main__':
    # 数据生成
    N = 500
    x = torch.randn(N, requires_grad=True)

    """
    #####################################################
    # 对凸二次函数进行求解，正定矩阵，求解最小值
    #####################################################
    # data_gen = Data_Gen(N)

    # 随机梯度法
    # sgd(x, data_gen)

    # bls算法
    bls(x, data_gen)
    """

    #####################################################
    # 对非凸二次函数进行求解，非正定矩阵，求解最小值
    #####################################################
    data_gen = Data_Gen(N, positive_definite=False)

    # 随机梯度法
    # sgd(x, data_gen)

    # bls算法
    bls(x, data_gen)

 

运算结果：

iter_num:  12931 search_time:  50  y_old:  21.942323684692383 y_new:  21.939422607421875
iter_num:  12932 search_time:  49  y_old:  21.939422607421875 y_new:  21.936918258666992
iter_num:  12933 search_time:  51  y_old:  21.936918258666992 y_new:  21.934120178222656
iter_num:  12934 search_time:  47  y_old:  21.934120178222656 y_new:  21.93170738220215
iter_num:  12935 search_time:  51  y_old:  21.93170738220215 y_new:  21.92693519592285
iter_num:  12936 search_time:  48  y_old:  21.92693519592285 y_new:  21.924362182617188
iter_num:  12937 search_time:  51  y_old:  21.924362182617188 y_new:  21.922771453857422
iter_num:  12938 search_time:  45  y_old:  21.922771453857422 y_new:  21.919511795043945
iter_num:  12939 search_time:  51  y_old:  21.919511795043945 y_new:  21.914203643798828
iter_num:  12940 search_time:  49  y_old:  21.914203643798828 y_new:  21.911758422851562
iter_num:  12941 search_time:  51  y_old:  21.911758422851562 y_new:  21.9085693359375
iter_num:  12942 search_time:  48  y_old:  21.9085693359375 y_new:  21.904415130615234
iter_num:  12943 search_time:  89  y_old:  21.904415130615234 y_new:  21.904300689697266
iter_num:  12944 search_time:  90  y_old:  21.904300689697266 y_new:  21.904294967651367

 

可以看到，对于非凸优化问题，bls算法虽然依旧获得由于sgd算法的结果，但是在运算迭代次数上却远远高于sgd算法；上面的非凸优化问题，随机梯度下降共迭代18296次，而bls算法迭代12944次，但是bls算法在每次迭代过程中都进行了50次左右的search，因此bls算法对于非凸优化问题在运行时间上是不占优势的。

 

不过对于bls算法，我们可以通过对其参数的修改优化其运算性能，比如将 c 设置为： c = 0.5

代码：

import random
import numpy as np
from scipy.linalg import orth
import torch

seed = 9999
random.seed(seed)
np.random.seed(seed)

torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True


class Data_Gen():
    def __init__(self, N, positive_definite=True):
        self.N = N

        # 不变的矩阵
        B = np.random.rand(N, 1)
        # 数据集，数据B矩阵
        self.B = torch.tensor(B, dtype=torch.float32)

        if positive_definite==True:
            # 正定矩阵的生成, A_
            X = np.diag(np.abs(np.random.rand(N))+1)
            U = orth(np.random.rand(N, N))
            A = np.dot(np.dot(U.T, X), U)
        else:
            # 非正定矩阵的生成，A
            M = np.random.rand(N, N)
            A = np.dot(M.T, M) + 0.01*np.eye(N)
        self.A = torch.tensor(A, dtype=torch.float32)

    def data_gen(self, x: torch.FloatTensor):
        """ 数据生成 """
        # 训练数据，x_data, x
        # x = torch.randn(N, requires_grad=True)
        N = x.size()[0]
        assert N==self.N, "向量长度不匹配"

        # 构建训练数据，非正定数据矩阵生成的y_data
        y=self.object_fun(self.A, self.B, x)
        return y

    def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
        if x.dim() == 1:
            x = torch.unsqueeze(x, 1)
        ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
        # print( torch.mm(A, x) )
        # print( torch.mm(x.T, torch.mm(A, x)) )
        # print( torch.mm(x.T, B) )
        return torch.squeeze(ans)


#####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
    # x = torch.randn(N, device="cuda:0", requires_grad=True)
    y = data_gen.data_gen(x)

    iter_num = 0
    while True:
        g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
        x.data.add_( -step*g )
        y_new = data_gen.data_gen(x)

        iter_num += 1
        print("iter_num: ", iter_num, "y_old: ", y.item(),  "y_new: ", y_new.item())
        if abs(y_new.item()-y.item()) < 0.00001:
            break
        else:
            y = y_new


#####################################################
#  回溯线搜索（Backtracking line search）
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
    iter_num = 0
    c = 0.5
    beta = 0.8
    while True:
        iter_num += 1
        y0 = data_gen.data_gen(x) 
        g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0]
        
        p = -1.0*g  # 求最小值，梯度下降，使用负梯度
        delta_f = g

        search_time = 0
        alpha_step = 1.0
        while True:
            y_new = data_gen.data_gen(x.detach() + alpha_step*p) 
            y_up = y0 + c*alpha_step*torch.dot(delta_f, p)

            if y_new.item() > y_up.item():
                search_time += 1
                alpha_step *= beta
            else:
                break
        x.data.add_( alpha_step*p )

        print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
        if abs(y_new.item()-y0.item()) < 0.00001:
            break


if __name__ == '__main__':
    # 数据生成
    N = 500
    x = torch.randn(N, requires_grad=True)

    """
    #####################################################
    # 对凸二次函数进行求解，正定矩阵，求解最小值
    #####################################################
    # data_gen = Data_Gen(N)

    # 随机梯度法
    # sgd(x, data_gen)

    # bls算法
    bls(x, data_gen)
    """

    #####################################################
    # 对非凸二次函数进行求解，非正定矩阵，求解最小值
    #####################################################
    data_gen = Data_Gen(N, positive_definite=False)

    # 随机梯度法
    # sgd(x, data_gen)

    # bls算法
    bls(x, data_gen)

 

运算结果：

iter_num:  3676 search_time:  53  y_old:  29.511341094970703 y_new:  29.50807762145996
iter_num:  3677 search_time:  34  y_old:  29.50807762145996 y_new:  29.432992935180664
iter_num:  3678 search_time:  53  y_old:  29.432992935180664 y_new:  29.379230499267578
iter_num:  3679 search_time:  47  y_old:  29.379230499267578 y_new:  29.374101638793945
iter_num:  3680 search_time:  51  y_old:  29.374101638793945 y_new:  29.368497848510742
iter_num:  3681 search_time:  62  y_old:  29.368497848510742 y_new:  29.3680362701416
iter_num:  3682 search_time:  70  y_old:  29.3680362701416 y_new:  29.367828369140625
iter_num:  3683 search_time:  82  y_old:  29.367828369140625 y_new:  29.367551803588867
iter_num:  3684 search_time:  90  y_old:  29.367551803588867 y_new:  29.367528915405273
iter_num:  3685 search_time:  98  y_old:  29.367528915405273 y_new:  29.367528915405273

将 c 设置为： c = 0.5，  将 beta 设置为：beta=0.1

代码：

import random
import numpy as np
from scipy.linalg import orth
import torch

seed = 9999
random.seed(seed)
np.random.seed(seed)

torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True


class Data_Gen():
    def __init__(self, N, positive_definite=True):
        self.N = N

        # 不变的矩阵
        B = np.random.rand(N, 1)
        # 数据集，数据B矩阵
        self.B = torch.tensor(B, dtype=torch.float32)

        if positive_definite==True:
            # 正定矩阵的生成, A_
            X = np.diag(np.abs(np.random.rand(N))+1)
            U = orth(np.random.rand(N, N))
            A = np.dot(np.dot(U.T, X), U)
        else:
            # 非正定矩阵的生成，A
            M = np.random.rand(N, N)
            A = np.dot(M.T, M) + 0.01*np.eye(N)
        self.A = torch.tensor(A, dtype=torch.float32)

    def data_gen(self, x: torch.FloatTensor):
        """ 数据生成 """
        # 训练数据，x_data, x
        # x = torch.randn(N, requires_grad=True)
        N = x.size()[0]
        assert N==self.N, "向量长度不匹配"

        # 构建训练数据，非正定数据矩阵生成的y_data
        y=self.object_fun(self.A, self.B, x)
        return y

    def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
        if x.dim() == 1:
            x = torch.unsqueeze(x, 1)
        ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
        # print( torch.mm(A, x) )
        # print( torch.mm(x.T, torch.mm(A, x)) )
        # print( torch.mm(x.T, B) )
        return torch.squeeze(ans)


#####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
    # x = torch.randn(N, device="cuda:0", requires_grad=True)
    y = data_gen.data_gen(x)

    iter_num = 0
    while True:
        g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
        x.data.add_( -step*g )
        y_new = data_gen.data_gen(x)

        iter_num += 1
        print("iter_num: ", iter_num, "y_old: ", y.item(),  "y_new: ", y_new.item())
        if abs(y_new.item()-y.item()) < 0.00001:
            break
        else:
            y = y_new


#####################################################
#  回溯线搜索（Backtracking line search）
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
    iter_num = 0
    c = 0.5
    beta = 0.1
    while True:
        iter_num += 1
        y0 = data_gen.data_gen(x) 
        g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0]
        
        p = -1.0*g  # 求最小值，梯度下降，使用负梯度
        delta_f = g

        search_time = 0
        alpha_step = 1.0
        while True:
            y_new = data_gen.data_gen(x.detach() + alpha_step*p) 
            y_up = y0 + c*alpha_step*torch.dot(delta_f, p)

            if y_new.item() > y_up.item():
                search_time += 1
                alpha_step *= beta
            else:
                break
        x.data.add_( alpha_step*p )

        print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
        if abs(y_new.item()-y0.item()) < 0.00001:
            break


if __name__ == '__main__':
    # 数据生成
    N = 500
    x = torch.randn(N, requires_grad=True)

    """
    #####################################################
    # 对凸二次函数进行求解，正定矩阵，求解最小值
    #####################################################
    # data_gen = Data_Gen(N)

    # 随机梯度法
    # sgd(x, data_gen)

    # bls算法
    bls(x, data_gen)
    """

    #####################################################
    # 对非凸二次函数进行求解，非正定矩阵，求解最小值
    #####################################################
    data_gen = Data_Gen(N, positive_definite=False)

    # 随机梯度法
    # sgd(x, data_gen)

    # bls算法
    bls(x, data_gen)

 

运算结果：

iter_num:  1838 search_time:  6  y_old:  83.01563262939453 y_new:  82.85948181152344
iter_num:  1839 search_time:  6  y_old:  82.85948181152344 y_new:  82.74000549316406
iter_num:  1840 search_time:  6  y_old:  82.74000549316406 y_new:  82.64784240722656
iter_num:  1841 search_time:  6  y_old:  82.64784240722656 y_new:  82.57584381103516
iter_num:  1842 search_time:  6  y_old:  82.57584381103516 y_new:  82.52399444580078
iter_num:  1843 search_time:  6  y_old:  82.52399444580078 y_new:  82.48124694824219
iter_num:  1844 search_time:  6  y_old:  82.48124694824219 y_new:  82.44764709472656
iter_num:  1845 search_time:  6  y_old:  82.44764709472656 y_new:  82.42279815673828
iter_num:  1846 search_time:  6  y_old:  82.42279815673828 y_new:  82.40233612060547
iter_num:  1847 search_time:  6  y_old:  82.40233612060547 y_new:  82.38795471191406
iter_num:  1848 search_time:  6  y_old:  82.38795471191406 y_new:  82.37630462646484
iter_num:  1849 search_time:  6  y_old:  82.37630462646484 y_new:  82.36550903320312
iter_num:  1850 search_time:  6  y_old:  82.36550903320312 y_new:  82.35576629638672
iter_num:  1851 search_time:  11  y_old:  82.35576629638672 y_new:  82.35576629638672

 

 

 

可以看到，对于非凸优化问题，如果使用bls算法，在追求运算速度的情况下必然要舍弃最终的运算结果性能，而追求运算结果的性能必然要花费大量的运算时间，因此可以说bls算法更适合于凸优化问题，而对于非凸问题，bls算法往往难以得到很好的性能表现。

 

 

 

 

===================================================

 

 

参考：

https://zhuanlan.zhihu.com/p/590013413

https://blog.csdn.net/jianti9962/article/details/121739041

https://www.cnblogs.com/fstang/p/4192735.html