LeetCode——二叉树遍历
先序
递归:
public static ArrayList<Integer> preorderTraversal(TreeNode root) {
ArrayList<Integer> array = new ArrayList<>();
if (root == null)
return array;
preorder(root, array);
return array;
}
public static void preorder(TreeNode root, ArrayList<Integer> array) {
if (root == null)
return;
array.add(root.val);
preorder(root.left, array);
preorder(root.right, array);
}
非递归:
public ArrayList<Integer> preorderTraversal(TreeNode root) {
ArrayList<Integer> array = new ArrayList<>();
if (root == null)
return array;
Stack<TreeNode> s = new Stack<>();
TreeNode node = root;
while (node != null || !s.empty()) {
while (node != null) {
//遍历到左子树下面,边遍历边保存
array.add(node.val);
s.push(node);
node = node.left;
}
if (!s.empty()) {
node = s.peek();
s.pop();
//进入右子树,再在下一步遍历左子树
node = node.right;
}
}
return array;
}
中序
递归:
public static ArrayList<Integer> inorderTraversal(TreeNode root) {
ArrayList<Integer> array = new ArrayList<>();
if (root == null)
return array;
inorder(root, array);
return array;
}
public static void inorder(TreeNode root, ArrayList<Integer> array) {
if (root == null)
return;
inorder(root.left, array);
array.add(root.val);
inorder(root.right, array);
}
非递归:
public static ArrayList<Integer> inorderTraversal(TreeNode root) {
ArrayList<Integer> array = new ArrayList<>();
if (root == null)
return array;
Stack<TreeNode> s = new Stack<>();
TreeNode node = root;
while (node != null || !s.empty()) {
while (node != null) {
s.push(node);
node = node.left;
}
if(!s.empty()){
node = s.peek();
array.add(node.val);
s.pop();
node = node.right;
}
}
return array;
}
后序
递归:
public static ArrayList<Integer> postorderTraversal(TreeNode root){
ArrayList<Integer> array = new ArrayList<>();
if(root == null)
return array;
posorder(root, array);
return array;
}
public static void posorder(TreeNode root, ArrayList<Integer> array){
if(root == null)
return;
posorder(root.left, array);
posorder(root.right, array);
array.add(root.val);
}
非递归
public static ArrayList<Integer> postorderTraversal(TreeNode root) {
ArrayList<Integer> array = new ArrayList<>();
if (root == null)
return array;
Stack<TreeNode> stack = new Stack<>();
//当前节点
TreeNode node = root;
//访问的前一个节点
TreeNode last = null;
while (node != null) {
stack.push(node);
//移到左子树最下面
node = node.left;
}
while (!stack.empty()) {
node = stack.peek();
stack.pop();
//如果右子树为空或右子树被访问过
if (node.right == null || node.right == last) {
array.add(node.val);
last = node;
} else {
//重新把当前点放进去
stack.push(node);
//读取右子树
node = node.right;
while (node != null) {
//把右子树的左子树递归放入
stack.push(node);
node = node.left;
}
}
}
return array;
}
层序
public static ArrayList<Integer> levelTraversal(TreeNode root) {
ArrayList<Integer> array = new ArrayList<>();
if(root == null)
return array;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
TreeNode node;
while(!queue.isEmpty()){
node = queue.peek();
array.add(node.val);
queue.poll();
if(node.left!=null)
queue.offer(node.left);
if(node.right!=null)
queue.offer(node.right);
}
return array;
}
Morris遍历算法
引用:https://www.jianshu.com/p/484f587c967c
Morris遍历法,能以O(1)的空间复杂度实现二叉树的中序遍历。
Morris遍历算法的步骤如下:
- 根据当前节点,找到其前序节点,如果前序节点的右孩子是空,那么把前序节点的右孩子指向当前节点,然后进入当前节点的左孩子。
- 如果当前节点的左孩子为空,打印当前节点,然后进入右孩子。
- 如果当前节点的前序节点其右孩子指向了它本身,那么把前序节点的右孩子设置为空,打印当前节点,然后进入右孩子。
代码:
public ArrayList<Integer> MorrisTraval(TreeNode root) {
ArrayList<Integer> res = new ArrayList<>();
if (root == null)
return res;
travel(root, res);
return res;
}
private void travel(TreeNode root, ArrayList<Integer> array) {
TreeNode node = root;
while (node != null) {
if (node.left == null) {
//左孩子为空,打印当前节点,然后进入右孩子
array.add(node.val);
node = node.right;
} else {
//找到其前序节点
TreeNode pre = getPredecessor(node);
if (pre.right == null) {
//如果前序节点的右孩子是空,那么把前序节点的右孩子指向当前节点,然后进入当前节点的左孩子
pre.right = node;
node = node.left;
} else if (pre.right == node) {
//当前节点的前序节点其右孩子指向了它本身,那么把前序节点的右孩子设置为空,打印当前节点,然后进入右孩子
pre.right = null;
array.add(node.val);
node = node.right;
}
}
}
}
//在二叉树中查找一个节点的前序节点。值得注意的是,前序节点的右指针一定是空的
private TreeNode getPredecessor(TreeNode node) {
TreeNode pre = node;
if (node.left != null) {
//如果该节点有左孩子,那么从左孩子开始,沿着右孩子指针一直想有走到底,得到的节点就是它的前序节点
pre = pre.left;
while (pre.right != null && pre.right != node) {
pre = pre.right;
}
}
return pre;
}
举例说明:
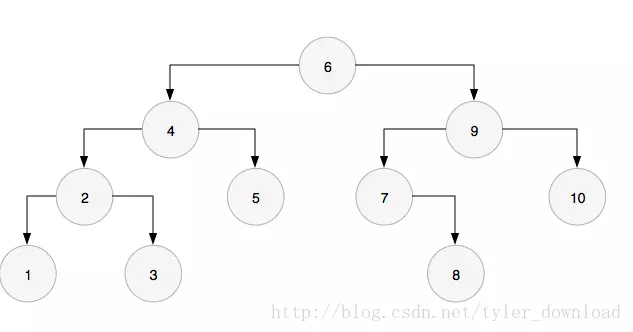
首先访问的是根节点6,得到它的前序节点是5,此时节点5的右孩子是空,所以把节点5的右指针指向节点6:
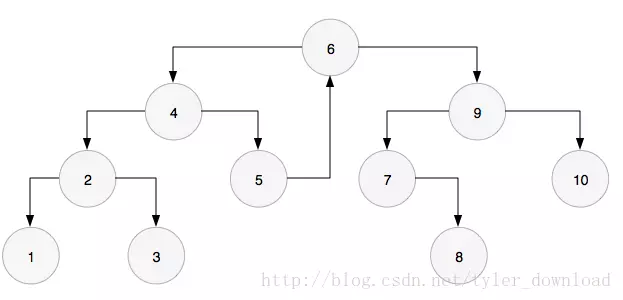
进入左孩子,也就到了节点4,此时节点3的前序节点3,右孩子指针是空,于是节点3的右孩子指针指向节点4,然后进入左孩子,也就是节点2

此时节点2的左孩子1没有右孩子,因此1就是2的前序节点,并且节点1的右孩子指针为空,于是把1的右孩子指针指向节点2,然后从节点2进入节点1:
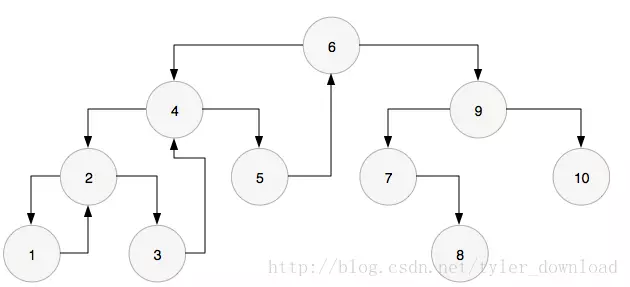
此时节点1没有左孩子,因此打印它自己的值,然后进入右孩子,于是回到节点2.根据算法步骤,节点2再次找到它的前序节点1,发现前序节点1的右指针已经指向它自己了,所以打印它自己的值,同时把前序节点的右孩子指针设置为空,同时进入右孩子,也就是节点3.于是图形变为:
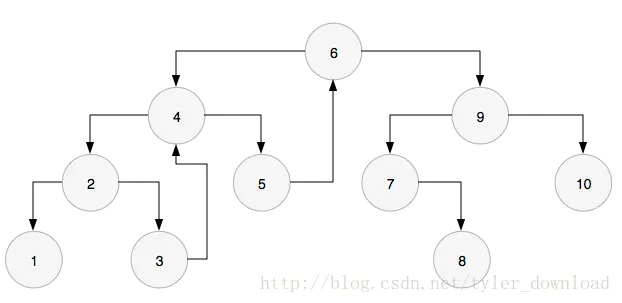
此时节点3没有左孩子,因此打印它自己的值,然后进入它的右孩子,也就是节点4. 到了节点4后,根据算法步骤,节点4先获得它的前序节点,也就是节点3,发现节点3的右孩子节点已经指向自己了,所以打印它自己的值,也就是4,然后把前序节点的右指针设置为空,于是图形变成:

接着从节点4进入右孩子,也就是节点5,此时节点5没有左孩子,所以直接打印它本身的值,然后进入右孩子,也就是节点6,根据算法步骤,节点6获得它的前序节点5,发现前序节点的右指针已经指向了自己,于是就打印自己的值,把前序节点的右指针设置为空,然后进入右孩子。
接下来的流程跟上面一样,就不再重复了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号