深度学习基础——感知机
转载自:原文地址
神经网络如下图所示:
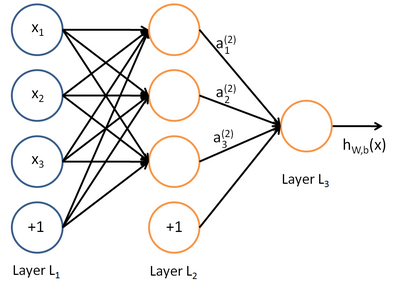
上图中每个圆圈都是一个神经元,每条线表示神经元之间的连接。我们可以看到,上面的神经元被分成了多层,层与层之间的神经元有连接,而层内之间的神经元没有连接。最左边的层叫做输入层,这层负责接收输入数据;最右边的层叫输出层,我们可以从这层获取神经网络输出数据。输入层和输出层之间的层叫做隐藏层。
感知器——神经网络的组成单元
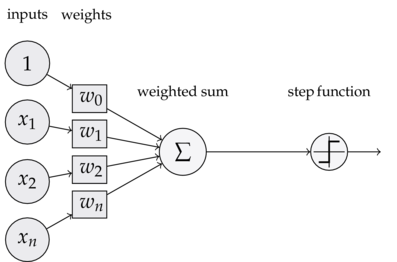
一个感知器有如下组成部分:

举例:用感知器实现and函数
我们设计一个感知器,让它来实现and运算。程序员都知道,and是一个二元函数(带有两个参数x1和x2),下面是它的真值表:
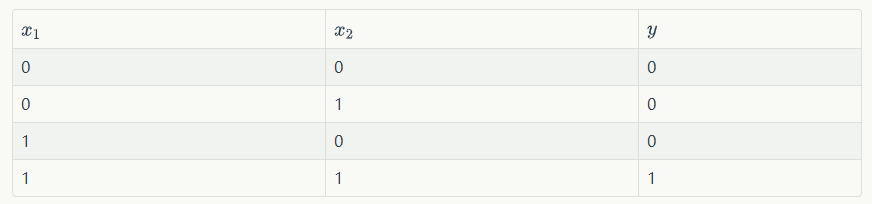
为了计算方便,我们用0表示false,用1表示true。
我们令w1=0.5,w2=0.5,b=-0.8,而激活函数就是前面写出来的阶跃函数,这时,感知器就相当于and函数。
输入真值表第一行,即x1=x2=0,则输出为:

即当x1=x2=0时,y=0,这是真值表的第一行。
举例2:用感知器实现or函数
同样,我们也可以用感知器来实现or运算。仅仅需要把偏置项的值设置为-0.3就可以了。我们验算一下,下面是or运算的真值表:
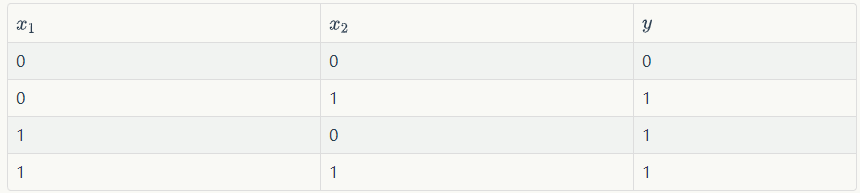
我们来验算第二行,这时的输入是x1=0,x2=1,带入公式(1):
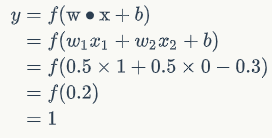
也就是当时x1=0,x2=1为1,即or真值表第二行。
感知器的其他功能
事实上,感知器不仅仅能实现简单的布尔运算。它可以拟合任何的线性函数,任何线性分类或线性回归问题都可以用感知器来解决。前面的布尔运算可以看作是二分类问题,即给定一个输入,输出0(属于分类0)或1(属于分类1)。如下面所示,and运算是一个线性分类问题,即可以用一条直线把分类0(false,红叉表示)和分类1(true,绿点表示)分开。
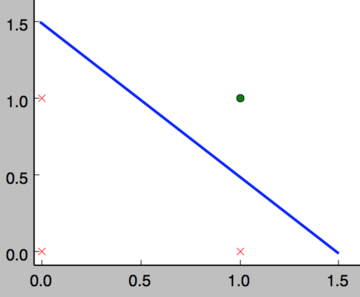
然而,感知器却不能实现异或运算,如下图所示,异或运算不是线性的,你无法用一条直线把分类0和分类1分开。

感知器训练
感知器训练算法:将权重项和偏置项初始化为0,然后,利用下面的感知器规则迭代的修改wi和b,直到训练完成。

其中
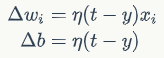
wi是与输入xi对应的权重项,b是偏置项。事实上,可以把b看作是值永远为1的输入xb所对应的权重。t是训练样本的实际值,一般称之为label。而y是感知器的输出值,它是根据公式(1)计算得出。\(\eta\)是一个称为学习速率的常数,其作用是控制每一步调整权的幅度。
每次从训练数据中取出一个样本的输入向量x,使用感知器计算其输出y,再根据上面的规则来调整权重。每处理一个样本就调整一次权重。经过多轮迭代后(即全部的训练数据被反复处理多轮),就可以训练出感知器的权重,使之实现目标函数。
编程实战:实现感知器
完整代码请参考GitHub:代码
下面是感知器类的实现,非常简单。只用到了基本的python(省去您去学习numpy的时间)。
class Perceptron(object):
def __init__(self, input_num, activator):
'''
初始化感知器,设置输入参数的个数,以及激活函数。
激活函数的类型为double -> double
'''
self.activator = activator
# 权重向量初始化为0
self.weights = [0.0 for _ in range(input_num)]
# 偏置项初始化为0
self.bias = 0.0
def __str__(self):
'''
打印学习到的权重、偏置项
'''
return 'weights\t:%s\nbias\t:%f\n' % (self.weights, self.bias)
def predict(self, input_vec):
'''
输入向量,输出感知器的计算结果
'''
# 把input_vec[x1,x2,x3...]和weights[w1,w2,w3,...]打包在一起
# 变成[(x1,w1),(x2,w2),(x3,w3),...]
# 然后利用map函数计算[x1*w1, x2*w2, x3*w3]
# 最后利用reduce求和
return self.activator(
reduce(lambda a, b: a + b,
map(lambda (x, w): x * w,
zip(input_vec, self.weights))
, 0.0) + self.bias)
def train(self, input_vecs, labels, iteration, rate):
'''
输入训练数据:一组向量、与每个向量对应的label;以及训练轮数、学习率
'''
for i in range(iteration):
self._one_iteration(input_vecs, labels, rate)
def _one_iteration(self, input_vecs, labels, rate):
'''
一次迭代,把所有的训练数据过一遍
'''
# 把输入和输出打包在一起,成为样本的列表[(input_vec, label), ...]
# 而每个训练样本是(input_vec, label)
samples = zip(input_vecs, labels)
# 对每个样本,按照感知器规则更新权重
for (input_vec, label) in samples:
# 计算感知器在当前权重下的输出
output = self.predict(input_vec)
# 更新权重
self._update_weights(input_vec, output, label, rate)
def _update_weights(self, input_vec, output, label, rate):
'''
按照感知器规则更新权重
'''
# 把input_vec[x1,x2,x3,...]和weights[w1,w2,w3,...]打包在一起
# 变成[(x1,w1),(x2,w2),(x3,w3),...]
# 然后利用感知器规则更新权重
delta = label - output
self.weights = map(
lambda (x, w): w + rate * delta * x,
zip(input_vec, self.weights))
# 更新bias
self.bias += rate * delta
将上述程序保存为perceptron.py文件,通过命令行执行这个程序,其运行结果为:
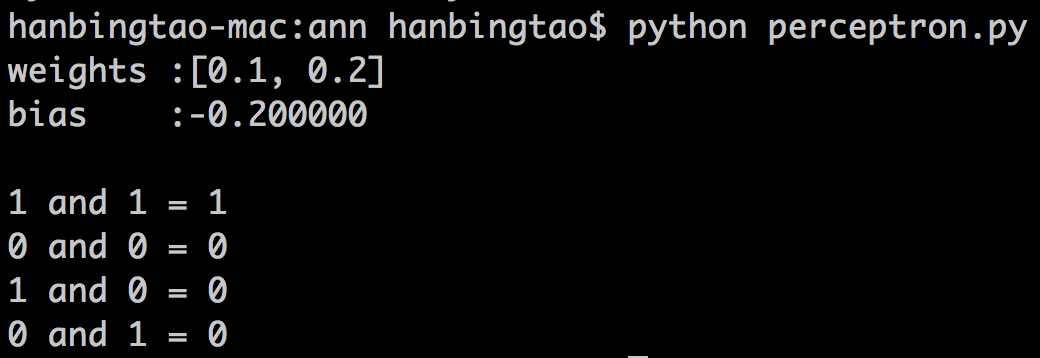
神奇吧!感知器竟然完全实现了and函数。读者可以尝试一下利用感知器实现其它函数。
多层感知机
因为单层感知机无法解决非线性可分问题——异或问题,所以引出“多层”的概念:使用多层感知机处理。下图就是一个两层感知机解决异或问题的示意图:

构建好上述网络以后,通过训练得到最后的分类面如下:

由此可见,多层感知机可以很好的解决非线性可分问题,我们通常将多层感知机这样的多层结构称之为是神经网络。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号