Codeforces Round #842 (Div. 2)

题目链接

A

核心思路：样例模拟出答案。

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3e5 + 10,INF=0x3f3f3f3f, mod = 998244353;
void solve()
{
	LL n;
	cin >> n;
	cout << n - 1 << endl;
}

int main()
{
	int T;
    T = 1;
	cin >> T;

	while (T--)
	{
		solve();
	}
}

---

B

核心思路：这个题目的关键是需要找出相对顺序，找出来需要我们操作的数。 我们可以操作的数就是不符合相对顺序的长度。总的来说这个题目还是有点玄学，就是属于有那个感觉了，但是不知道怎么去操作。注意别想复杂就好了。

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3e5 + 10,INF=0x3f3f3f3f, mod = 998244353;
int a[N];
void solve()
{
	int n, k;
	cin >> n >> k;
	for (int i = 1;i <= n;i++)
	{
		cin >> a[i];
	}
	int cnt = 1;
	for (int i = 1;i <= n;i++)
	{
		if (a[i] == cnt)
		{
			cnt++;
		}
	}
	double t = (double)(n - cnt + 1) / k;
	double ans = ceil(t);
	cout << ans << endl;
}

int main()
{
	int T;
    T = 1;
	cin >> T;

	while (T--)
	{
		solve();
	}
}

---

C

核心思路：这个题目刚开始确实不知道怎么去构造，但是我们通过模拟样例可以发现，应该是需要构造的数列p中某一个数不可以超过2可以等于2.这是我们发现的第一个性质，然后再去思考另外一种无解的情况，也就是1 1.这个又是为什么无解呢，其实我们可以发现前i个位置，我们可以检查前i个数出现的次数，如果是大于i那么也肯定无解。因为我们的位置塞不下这么多数了。

好了，讨论了无解的情况，接下来去像怎么去构造有解的情况。

• 某个数出现的次数为2的构造：我们可以假设是i，j这两个位置出现了次数是2的情况。那我们可以寻找第一个小于等于b[i]的那个没有出现的数进行这个位置的填补。
• 然后其他次数为1的构造：这个我们可以利用max的性质,也就是\(max(x,x)=x,可重复贡献性\)。就是两个位置都填b[i].

下面看下模拟的实例模拟吧。

需要构造的数组p：1 3 4 3 5
ans1:1 2 4 3 5
ans2:1 3 4 2 5

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3e5 + 10,INF=0x3f3f3f3f, mod = 998244353;
int a[N],ans1[N],ans2[N];//st里面存的是st[x]=y.
void solve()
{
	int n;
	cin >> n;
	for (int i = 1;i <= n;i++)
		cin >> a[i];
	vector<int> v;//这个里面放的是从来没有出现的数.
	map<int, int> mp,st;
	for (int i = 1;i <= n;i++)
	{
		mp[a[i]]++;
		if (mp[a[i]] > 2)
		{
			cout << "NO" << endl;return;
		}
	}
	int cur = 0;
	for (int i = 1;i <= n;i++)
	{
		cur += mp[i];
		if (!mp[i])
		{
			v.push_back(i);
		}
		if (cur > i)
		{
			cout << "NO" << endl;
			return;
		}
	}
	for (int i = 1;i <= n;i++)
	{
		if (mp[a[i]] ==  1)
		{
			ans1[i] = a[i];
			ans2[i] = a[i];
			continue;
		}
		if (!st[a[i]])
		{
			auto it = lower_bound(v.begin(), v.end(), a[i]);
			if (it == v.begin())
			{
				cout << "NO" << endl;
				return;
			}
			it--;
			ans1[i] = *it;
			st[a[i]] = ans1[i];
			ans2[i] = a[i];
			v.erase(it);
		}
		else
		{
			ans1[i] = a[i];
			ans2[i] = st[a[i]];
		}
	}
	cout << "YES" << endl;
	for (int i = 1;i <= n;i++)
	{
		cout << ans1[i] << " ";
	}
	cout << endl;
	for (int i = 1;i <= n;i++)
	{
		cout << ans2[i] << " ";
	}
	cout << endl;
}

int main()
{
	int T;
	cin >> T;
	while (T--)
	{
		solve();
	}
}

其实对于构造问题，二分求我们的构造的数用得比较多.

---

D

核心思路：这是一个求逆序对的题目，所以我们可以联想置换环来进行求解。

现在引入置换环的一些前置知识吧：

置换环可以得到数组排序的一个最小次数，主要思想是：将我们的每个节点指向其排序后应该存放的位置，最终首尾相接形成一个环，那么数组排序的最小的次数就是数组的长度-环的数目。

所以我们在处理置换环的问题可以看成图论的问题。

但是这个题目还有一个性质：那就是相邻的两个环达到我们题目所需的条件只需要n-cur-1.

下面看ygg的图：

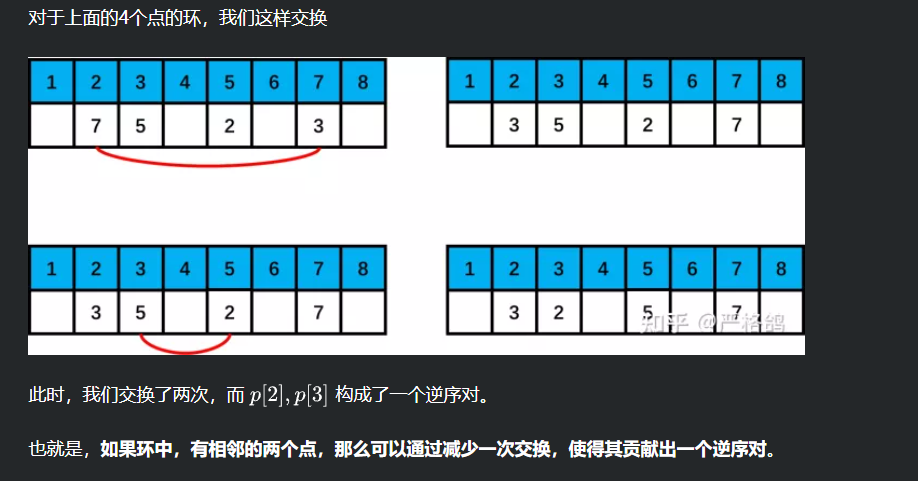
所以这个问题也就基本解决了。

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3e5 + 10,INF=0x3f3f3f3f, mod = 998244353;
int n, p[N], vis[N];
map<int, bool> ring;
bool flag = 0;
void dfs(int u)
{
	if (vis[u])
		return;
	int v = p[u];//这里表示的是u到v的一条边。
	ring[u] = 1;
	vis[u] = 1;
	if (ring[u - 1] || ring[u + 1])
		flag = 1;//相邻的位置有环.
	dfs(v);
}
void solve()
{
	cin >> n;
	for (int i = 1;i <= n;i++)
		cin >> p[i];
	memset(vis, 0, sizeof vis);
	int cur = 0;
	flag = 0;
	for (int i = 1;i <= n;i++)
	{
		if (!vis[i])
		{
			cur++;
			ring.clear();
			dfs(i);

		}
	}
	if (flag)
	{
		cout << n - cur - 1 << endl;
	}
	else
		cout << n - cur + 1 << endl;
}

int main()
{
	int T;
	cin >> T;
	while (T--)
	{
		solve();
	}
}