ST表

ST表

作用：ST表是为了解决可重复贡献性问题的数据结构，算是一种比较基本的数据结构吧。

Q：什么是可重复性贡献问题呢？

A：可重复贡献问题 是指对于运算 ，满足 ，则对应的区间询问就是一个可重复贡献问题。例如，最大值有 \(max(x,x)=x\)，gcd 有\(gcd(x,x)=x\) ，所以 RMQ 和区间 GCD 就是一个可重复贡献问题。像区间和就不具有这个性质，如果求区间和的时候采用的预处理区间重叠了，则会导致重叠部分被计算两次，这是我们所不愿意看到的。另外， 还必须满足结合律才能使用 ST 表求解。

RMQ定义：RMQ 是英文 Range Maximum/Minimum Query 的缩写，表示区间最大（最小）值。解决 RMQ 问题有很多种方法，可以参考 RMQ 专题。

其实像ST表解决不修改的最值查询问题是要优于线段树和树状数组的

下面浅谈下我对于ST表的理解吧：

其实他就和树状数组的思维是差不多的，也就是把我们的区间对半砍，然后分别去查询。有点类似于递归分治的思想在里面吧。

下面聊一聊他的一些初始化操作和 查询操作。

首先看我们Max数组的一个定义：\(Max[i][j]表示的是从i开始的，区间的长度是2^j,也就是区间右端点是i+2^j-1的区间的最大值\)

所以先看Max数组怎么进行预处理吧。

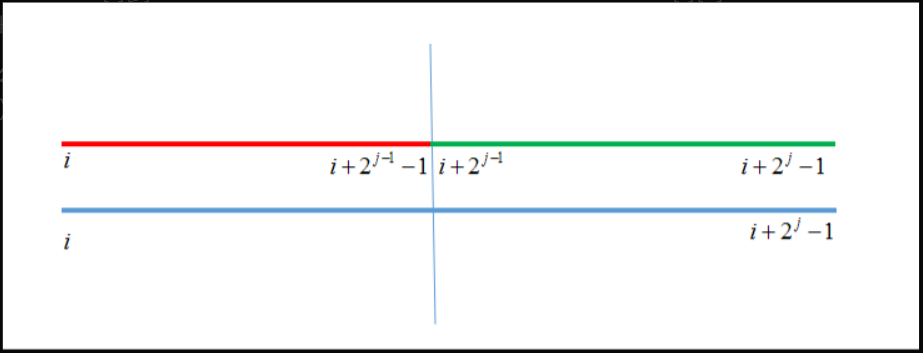
就是和这张图所示，把我们的区间对半砍分别取最大值。这样可保证不重不漏。
然后就是查询操作了，其实也很基础。

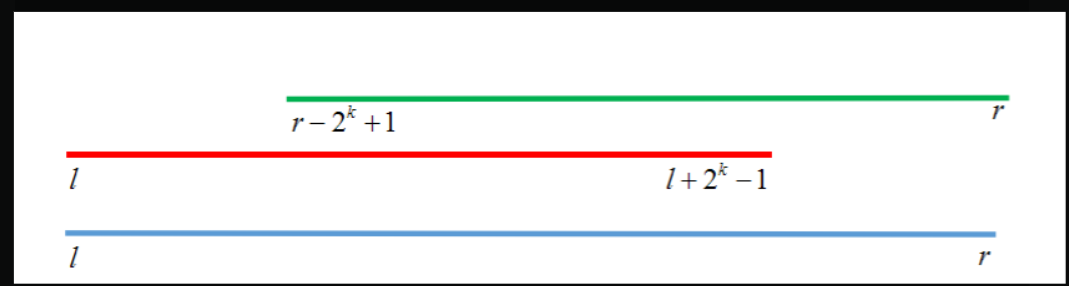
这个和线段树有点像吧，为了保证不遗漏，所以重复一点也没有问题。
ok，其实先学了高级数据结构学这个还是比较简单易懂的。
时间复杂度：\(O(nlogn)\)

其实我个人认为st表就是一个倍增dp

模板题

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3e6 + 10,INF=0x3f3f3f3f;
int n,m, ans = -INF;
LL a[N];
int Max[N][21];
int query(int l, int r)
{
    int k = log2(r - l + 1);//r-l+1是区间长度.
    return max(Max[l][k], Max[r - (1 << k) + 1][k]);//这里加1是为了保证区间的长度是(1<<k).
}

inline int read()
{
    char c = getchar();int x = 0, f = 1;
    while (c < '0' || c>'9') { if (c == '-')f = -1;c = getchar(); }
    while (c >= '0' && c <= '9') { x = x * 10 + c - '0';c = getchar(); }
    return x * f;
}
int main()
{
#ifdef WIN32
    freopen("a.in", "r", stdin);
#endif
    int n = read(), m = read();
    for (int i = 1;i <= n;i++)
        Max[i][0] = read();
    for (int j = 1;j <= 21;j++)//先枚举区间长度，在枚举左端点。这个和区间dp是一个道理,经典的从2开始枚举长度.
    {
        for (int l = 1;l + (1 << j) - 1 <= n;l++)//这里是将整个区间对半砍.
        {
            Max[l][j] = max(Max[l][j - 1], Max[l+(1<<(j-1))][j - 1]);//这里是因为左边的区间是[l,l+(1<<(j-1))-1],所有右边理所应当是[l+(1<<(j-1)),r].
        }
    }
    while (m--)
    {
        int l = read();
        int r = read();
        printf("%d\n", query(l, r));//别用cout，太慢了会导致超时.
    }
}

模板提2

核心思路

这里我们发现其实只有两个操作，一个数直接查询最后几个数，然后就是把数插在末尾。我们可以发现的这个修改的操作是可以使用st表的，因为我们只需要改下f的定义就好了，\(f[i][k]表示的是以i作为右端点，长度为2^k的区间\)。

这样我们就可以发现的是就算插入一个数，我们也只需要多更新一个位置就好了。因为前面我们是完全可以保证这是正确的。要注意下change函数这个地方。

for(int i=1;(u-(1<<i))>=0;i++)
	f[u][i]=max(f[u][i-1],f[u-(1<<(i-1))][i-1]);

好吧，是我对于操作还不够熟悉，没什么需要注意的。