SGR——Learning from Shortcut A Shortcut-guided Approach for Graph Rationalization【从捷径中学习：一种基于捷径引导的图合理化方法】

论文信息

论文标题：Learning from Shortcut A Shortcut-guided Approach for Graph Rationalization
论文作者：Linan_Yue , Qi Liu, Ye Liu, Weibo Gao, Chao Song
论文来源：ICLR'2024
发布时间：2024
论文地址：link
论文代码：link

1 研究问题&&研究动机

1.1 研究动机（Research Motivation）

1. 图神经网络的核心价值与痛点

• 核心价值：GNNs 在图分类任务（如分子属性预测、文本情感分析、 motif 类型识别）中表现卓越，已成为处理图结构数据的主流模型。

• 关键痛点：GNNs 的预测过程具有 “黑箱” 特性，缺乏可解释性 —— 用户无法知晓模型基于图中哪些关键信息（节点 / 边）做出决策，限制了其在高可靠性要求场景（如药物研发、医疗诊断）的应用。

2. 图合理化方法的现状与缺陷

• 图合理化的目标：通过提取原图的小子集（即 “理据，Rationale”，如关键节点、核心边），为 GNN 的预测结果提供直观解释，是解决 GNN 可解释性的核心方向。

• 现有方法的核心缺陷：

  • 易依赖 “捷径（Spurious Correlations）”：现有图合理化方法（如 DIR、DisC、GREA 等）倾向于利用数据中虚假的关联（而非真实的因果关系）生成理据。例如训练集中 “Cycle motif 与 Tree base 高频共现”，模型会误将 Tree base 当作预测 Cycle motif 的 “理据”。

  • 泛化能力差：在同分布数据上表现优异，但面对 “分布外（OOD）数据”（如测试集中 “Cycle motif 与 Wheel base 搭配”）时，预测准确率大幅下降，理据解释完全失效。

  • 未明确利用捷径信息：现有去偏方法多假设 “捷径未知”，通过构建隐式环境来提取不变理据，但未直接捕获和利用捷径信息，去偏效果有限。

3. 关键发现：捷径特征的易学习性

  文献（Arpit et al., 2017; Nam et al., 2020 等）验证：捷径特征比理据特征更易被模型学习—— 模型在训练初期会优先记忆捷径信息以快速拟合训练数据，而非学习输入与标签间的真实因果关系。这一发现为 “主动捕获捷径、并基于捷径区分理据与非理据” 提供了核心依据。

1.2 研究问题（Research Question）

1. 如何设计一种高效的方法，主动捕获数据中的捷径信息（无需人工标注捷径节点）？

2. 如何利用捕获的捷径信息，让模型明确区分 “理据（与标签有真实因果关系）” 和 “非理据（编码捷径信息）”？

3. 如何进一步提取 “跨环境不变的理据”—— 即不受捷径影响、在分布外数据中仍能稳定支撑预测的核心结构，提升模型的可解释性与泛化能力？

2 捷径引导的图合理化（Hortcut-Guided Graph Rationalization）

2.1 问题定义（Problem Definition）

核心目标

  针对图分类任务，明确图合理化的核心任务边界，为后续方法设计提供清晰的问题框架。

输入与输出定义

• 输入：单图实例 $g=(V, E)$（$V$ 为节点集，$E$ 为边集），对应的图级真实标签 $y$，数据集 $D_G = \{(g, y)\}$；邻接矩阵 $A \in \{0,1\}^{|V| \times |V|}$（表征节点间连接关系）。

• 中间输出：理据掩码向量 $M \in \mathbb{R}^N$（$N$ 为节点数，$M_i$ 表示第 $i$ 个节点被选为理据的概率）。

• 核心输出：

  1. 理据子图表征 $h_r$：通过公式 $h_r = \text{READOUT}(M \odot \text{GNN}_g(g))$ 计算，其中 $\text{GNN}_g(\cdot)$ 为任意 GNN 编码器（如 GIN），$\odot$ 为元素积，$\text{READOUT}$ 为图级表征聚合操作（本文采用均值池化）。

  2. 任务预测结果：基于 $h_r$ 完成图分类（如 motif 类型预测、分子属性预测）。

实例说明

  以图 1 的 motif 类型预测为例，目标是预测图的 motif 标签（Cycle/House），同时将真实决定标签的 Cycle/House 结构识别为理据，排除 Tree/Wheel 等无关 base 子图的干扰。

  

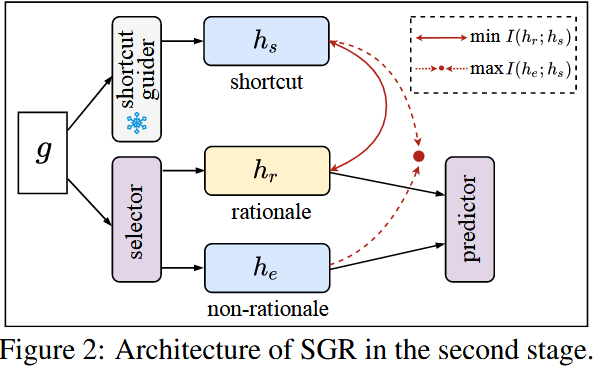
2.2 SGR 架构（Architecture of SGR）

整体框架

  SGR 通过两阶段训练实现 “从捷径中学习”，第二阶段为核心执行流程，包含捷径引导器（Shortcut Guider）、选择器（Selector）、预测器（Predictor） 三大模块，核心逻辑是：冻结第一阶段训练好的捷径引导器，利用其生成的捷径信息，指导理据与非理据的区分，最终提取跨环境不变理据。

  

2.2.1 捷径引导器（Shortcut Guider）

核心功能

  主动捕获数据中的捷径信息，生成可靠的捷径表征，为后续理据区分提供 “参考标准”。

设计依据

  基于关键发现：捷径特征比理据特征更易学习，模型训练初期学到的特征更倾向于捷径，因此通过早停策略可优先捕获捷径信息。

训练流程

1. 模型结构：采用任意 GNN 编码器（如 GCN）作为核心，配合 READOUT 操作和分类器 $\Phi_s(\cdot)$。

2. 公式定义：

   • 节点表征：$H_s = \text{GNN}_s(g)$（$H_s \in \mathbb{R}^{N \times d}$，d 为隐藏层维度）。

   • 图级捷径表征：$h_s = \text{READOUT}(H_s)$（$h_s \in \mathbb{R}^d$）。

   • 标签预测：$\hat{y}_s = \Phi_s(h_s)$。

3. 损失函数：交叉熵损失 $\mathcal{L}_s = \mathbb{E}_{(g,y) \sim D_G}[l(\hat{y}_s, y)]$（$l(\cdot)$ 为交叉熵损失函数）。

4. 关键操作：仅训练少量 epoch（如 2-3 个 epoch），确保模型捕获捷径而非理据；训练完成后冻结参数，用于第二阶段生成捷径表征。

2.2.2 选择器（Selector）

核心功能

  将原始输入图拆分为理据子图和非理据子图，并分别生成对应的图级表征。

执行步骤

1. 生成理据掩码：$M = \sigma(\Phi_m(\text{GNN}_m(g)))$，其中 $\Phi_m(\cdot)$ 将节点编码为理据选择分数，$\sigma$ 为 sigmoid 函数（输出概率值）。

2. 提取节点表征：通过 GNN 编码器 $\text{GNN}_g(g)$ 生成原始图的节点表征 $H_g$。

3. 拆分节点表征：

   • 理据节点表征：$M \odot H_g$（仅保留高概率理据节点的信息）。

   • 非理据节点表征：$(1-M) \odot H_g$（保留低概率理据节点的信息，即潜在捷径载体）。

4. 生成图级表征：通过 READOUT 操作聚合得到：

   • 理据子图表征：$h_r = \text{READOUT}(M \odot H_g)$。

   • 非理据子图表征：$h_e = \text{READOUT}((1-M) \odot H_g)$。

2.2.3 基于互信息估计的捷径学习（Learning From Shortcut by MI Estimation）

核心目标

  让理据表征剔除捷径信息、非理据表征编码全部捷径信息，明确区分 “真实理据” 与 “捷径载体”。

互信息（MI）的核心作用

  互信息 $I(X;Y)$ 衡量两个变量的相互依赖程度，本文通过 MI 的 “最小化” 与 “最大化” 实现双向约束：

• • 最小化 $I(h_r; h_s)$：让理据表征 $h_r$ 与捷径表征 $h_s$ 尽可能独立，剔除理据中的捷径信息。

  • 最大化 $I(h_e; h_s)$：让非理据表征 $h_e$ 与捷径表征 $h_s$ 尽可能相关，使非理据成为捷径的 “替身”。

实现方法

1. MI 最小化：采用 CLUB_NCE 方法（CLUB 的变体），通过估计 MI 的上界并最小化，实现 $h_r$ 与 $h_s$ 的去关联。

2. MI 最大化：采用 InfoNCE 方法，通过对比学习最大化 $h_e$ 与 $h_s$ 的关联程度。

3. 损失函数：$\mathcal{L}_{shortcut} = I(h_r; h_s) - I(h_e; h_s)$（通过优化该损失实现双向约束）。

2.2.4 预测器（Predictor）

核心功能

  基于理据表征完成任务预测，同时通过环境迁移策略提取 “跨环境不变理据”，提升模型泛化能力。

执行流程

1. 基础预测与损失：

   • 理据直接预测：$\hat{y}_r = \Phi_p(h_r)$（$\Phi_p(\cdot)$ 为共享分类器）。

   • 基础损失：$\mathcal{L}_r = \mathbb{E}_{(g,y) \sim D_G}[l(\hat{y}_r, y)]$（保证理据的预测准确性）。

2. 环境迁移与不变性约束：

   • 环境定义：将编码了捷径信息的非理据表征 $h_e$ 视为 “环境”。

   • 环境迁移构造：对批量样本 $\{(h_r^i, h_e^i, y^i)\}_{i=1}^K$，将每个 $h_r^i$ 与批量中其他所有 $h_e^j (j \neq i)$ 组合，得到 $h^{i,j} = h_r^i + h_e^j$（模拟不同环境下的理据分布）。

   • 迁移预测损失：$\hat{y}^{i,j} = \Phi_p(h^{i,j})$，损失 $\mathcal{L}_e = \mathbb{E}_i[\mathbb{E}_j[l(\hat{y}^{i,j}, y)]]$（保证理据在不同环境下的预测准确性）。

3. 跨环境稳定性损失：

   • 目标：让环境迁移后的预测结果与原始理据预测结果一致，确保理据不受环境（捷径）影响。

   • 损失计算：$\mathcal{L}_{diff} = \mathbb{E}_i[\mathbb{E}_j[\mathcal{D}_f(\hat{y}_r^i; \hat{y}^{i,j})] + \text{Var}_j[\mathcal{D}_f(\hat{y}_r^i; \hat{y}^{i,j})]]$，其中 $\mathcal{D}_f(\cdot)$ 为平方欧氏距离，通过最小化均值和方差保证预测稳定性。

2.3 训练与推理（Training and Inference）

训练阶段

  总损失函数 融合多维度约束，确保理据的 “准确性、去捷径性、跨环境稳定性、稀疏性”，总损失为：

    $\mathcal{L}_{sgr} = \mathcal{L}_r + \mathcal{L}_e + \lambda_{diff}\mathcal{L}_{diff} + \lambda_{shortcut}\mathcal{L}_{shortcut} + \lambda_{sp}\mathcal{L}_{sp}$

• 各组件作用：

  • $\mathcal{L}_r$：理据预测准确性约束。

  • $\mathcal{L}_e$：环境迁移下的预测准确性约束。

  • $\lambda_{diff}\mathcal{L}_{diff}$：跨环境稳定性约束（$\lambda_{diff}=0.1$）。

  • $\lambda_{shortcut}\mathcal{L}_{shortcut}$：捷径区分约束（$\lambda_{shortcut}=0.01$）。

  • $\lambda_{sp}\mathcal{L}_{sp}$：理据稀疏性约束（$\lambda_{sp}=1.0$），其中 $\mathcal{L}_{sp} = \left| \frac{1}{N}\sum_{i=1}^N M_i - \alpha \right|$，$\alpha$ 为预定义稀疏度（如 MolHIV 取 0.1，MolBBBP 取 0.5），确保理据是原图的小子集。

推理阶段：核心逻辑

  仅使用理据子图表征 $h_r$ 进行预测，因为 $h_r$ 已剔除捷径信息、且在不同环境下稳定，能为预测结果提供可靠解释。

3 实验

3.1 数据集（Datasets）

  核心目标：覆盖合成数据集（可控捷径强度，验证方法有效性）与真实数据集（贴近实际场景，验证泛化能力），共 10 个数据集，具体信息如下：

数据集类型	名称	任务场景	数据构造与关键设置	统计信息（核心指标）
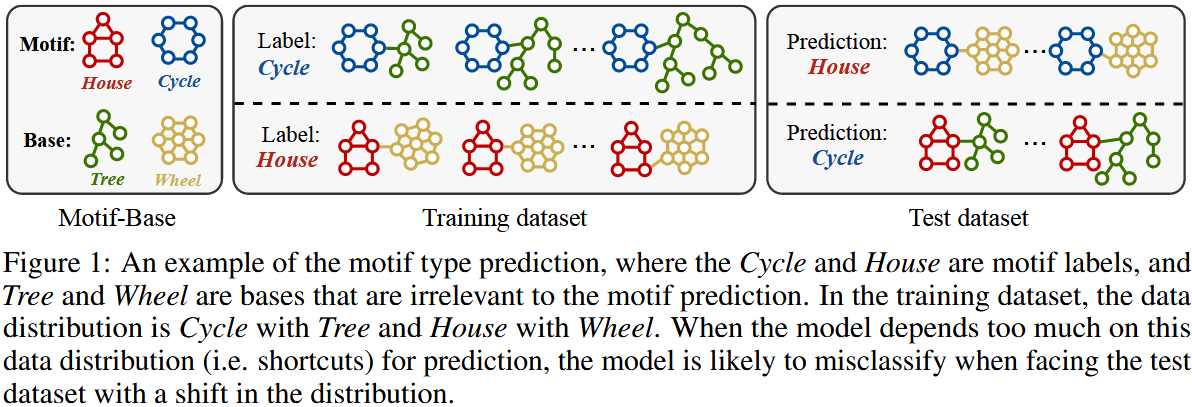
合成数据集	Spurious-Motif（4 个变体）	Motif 类型预测	- 每个图含 “motif 子图（理据，如 Cycle/House/Crane）” 和 “base 子图（非理据，如 Tree/Wheel/Ladder）”，标签仅由 motif 决定。   - 训练集：通过参数$b$控制捷径强度（$b=0.5,0.7,0.9$），P~(E)=b×I(E=R)+21−b​×I(E=R)，$b$越大捷径越强；额外构造 Cycle-Tree 变体（含平衡数据 + 1000 个 Cycle-Tree 偏置数据）。   - 测试集：无偏分布（$b=1/3$），验证 OOD 泛化能力。	- 类别数：3   - 训练 / 验证 / 测试集规模：3000/3000/6000（Cycle-Tree 为 4000/4000/6000）   - 平均节点数：28.9-30.8   - 平均边数：42.0-45.9
真实数据集	Graph-SST2	文本情感分析（图分类）	- 将 SST2 文本转换为图结构，按节点平均度数划分训练 / 测试集（训练集节点度数 > 测试集），构造分布偏移。	- 类别数：2   - 训练 / 验证 / 测试集规模：28327/3147/12305   - 平均节点数：13.7   - 平均边数：25.3
真实数据集	OGBG（5 个分子数据集）	分子属性预测	- 含 MolHIV、MolToxCast、MolBACE、MolBBBP、MolSIDER，默认按 scaffold 拆分数据集（不同拆分的分子结构差异大）。	- 类别数：2-617（MolToxCast 最多）   - 训练集规模：1141-32901   - 平均节点数：18.8-34.1   - 平均边数：19.3-36.9

数据集作用

• 合成数据集（Spurious-Motif）：可精准控制捷径强度，验证方法 “去捷径、提理据准确性” 的核心能力。

• 真实数据集（Graph-SST2/OGBG）：验证方法在实际任务中的泛化性能，贴近工业应用场景。

3.2 对比基线（Baselines）

分类与选择依据：覆盖 “经典 GNN 模型”“主流图合理化方法”，确保对比的全面性与针对性，具体如下：

基线类型	名称	核心特点	实现细节
经典 GNN（无解释性）	GCN（Kipf & Welling, 2017）	图卷积网络基础模型，无专门理据提取模块	作为基准模型，验证 “图合理化方法” 相对纯预测模型的优势
经典 GNN（无解释性）	GIN（Xu et al., 2019）	基于图同构网络，表达能力更强，无专门理据提取模块	同上，与 GCN 互补，覆盖不同 GNN 编码器
图合理化方法（去偏类）	DIR（Wu et al., 2022）	拆分理据 / 非理据子图，显式将非理据子图作为环境	与 SGR 核心思路相近，对比 “显式环境” 与 SGR“捷径引导 + 隐式环境” 的差异
图合理化方法（去偏类）	DisC（Fan et al., 2022）	拆分理据 / 非理据，将非理据表征作为环境，选择边作为理据	对比 “边理据” 与 SGR “节点理据” 的效果
图合理化方法（去偏类）	GREA（Liu et al., 2022）	拆分理据 / 非理据，将非理据表征作为环境，选择节点作为理据	与 SGR 理据类型一致，对比 “无捷径引导” 与 “有捷径引导” 的差异
图合理化方法（去偏类）	CAL（Sui et al., 2022）	拆分理据 / 非理据，将非理据表征作为环境，选择节点 + 边作为理据	对比 “混合理据” 与 SGR “节点理据” 的效果
图合理化方法（信息瓶颈类）	GSAT（Miao et al., 2022）	基于信息瓶颈原理，学习稀疏注意力选择理据，不考虑非理据信息	验证 “引入非理据 + 捷径信息” 的必要性
图合理化方法（解纠缠类）	DARE（Yue et al., 2022）	解纠缠 + MI 最小化提取理据，无专门捷径处理模块	对比 “仅 MI 最小化” 与 SGR“MI 双向约束 + 捷径引导” 的差异

统一设置

  所有基线与 SGR 均采用 GCN/GIN 作为图编码器（保证公平性），使用相同优化器（Adam）与超参数搜索范围。

3.3 实验内容、结果与结论

实验 1：验证 GNN 是否在训练初期学习捷径（核心假设验证）

实验目标

  验证 “捷径特征比理据特征更易学习，GNN 在训练初期优先捕获捷径” 的核心假设，为 SGR 的早停策略提供依据。

实验设计

1. 数据集：Spurious-Motif（含偏置训练集 + 偏置 / 无偏测试集）、Cycle-Tree 变体（含平衡数据 + 偏置数据）。

2. 模型：GCN、GIN（无任何去偏处理）。

3. 指标：训练损失、训练准确率、偏置 / 无偏测试集准确率。

实验结果

观测维度	具体结果
偏置 / 无偏测试集性能	- 偏置测试集：GCN/GIN 准确率接近 100%（充分利用捷径）； - 无偏测试集：性能显著下降（$b=0.9$时准确率仅 35%-38%）； - 趋势：$b$越大（捷径越强），偏置测试集性能越高，无偏测试集性能越低。
训练损失与准确率	- 偏置数据：训练 2 个 epoch 后损失趋近 0，准确率快速达到高值； - 平衡数据：训练多个 epoch 后损失才收敛，准确率提升缓慢（图 3 (b)(c)、图 8）。
捷径引导器有效性（MolBACE）	- 训练 1-3 个 epoch：SGR 性能随 epoch 增加而提升（捷径引导器捕获捷径）； - 训练 > 3 个 epoch：SGR 性能下降（捷径引导器开始学习理据，偏离目标）。

结论

• GNN 确实优先学习捷径（恶性偏置），且捷径强度越大，模型对捷径的依赖越强。

• 训练初期（2-3 个 epoch）的模型能有效捕获捷径信息，验证了 SGR 早停策略的合理性。

实验 2：整体性能对比（任务预测准确率）

实验目标

  验证 SGR 在 “任务预测准确性” 上是否优于经典 GNN 与主流图合理化基线。

实验设计

1. 数据集：所有 10 个数据集（Spurious-Motif、Graph-SST2、OGBG）。

2. 指标：

   • Spurious-Motif/Graph-SST2：ACC（准确率）；

      

   • OGBG：ROC-AUC（分子属性预测常用指标）。

3. 对比对象：所有基线模型（GCN、GIN、DIR、DisC 等）。

实验结果

数据集类型	核心结果
Spurious-Motif（无偏测试集）	- SGR 在所有变体（$b=0.5,0.7,0.9$、Cycle-Tree）中表现最优； - 例如 Cycle-Tree 变体：SGR（GIN backbone）准确率 58.01%，显著高于第二名 DisC（48.82%）。
Graph-SST2	- SGR（GIN backbone）ACC=83.86%，GCN backbone ACC=83.78%，均优于所有基线（DARE 最高 83.20%）。
OGBG	- 所有 5 个数据集上 SGR 均优于基线； - 代表案例：MolHIV（GIN backbone）：SGR ROC-AUC=79.45%，比 GIN（74.47%）提升 4.98%，比 DARE（78.36%）提升 1.09%。

结论

• SGR 显著优于经典 GNN：证明 “去捷径 + 理据提取” 能提升模型泛化能力（尤其 OOD 场景）。

• SGR 优于主流图合理化基线：说明 “主动捕获捷径 + 基于 MI 区分理据 / 非理据” 的思路有效，相比 “隐式去偏”“信息瓶颈” 等方法更具优势。

• 基线对比洞察：DIR 性能较差（显式环境丢失上下文），DisC/GREA/CAL 性能中等（隐式环境有效），GSAT/DARE 性能接近但不及 SGR（无捷径引导）。

实验 3：理据准确性对比（Precision@5）

实验目标

  验证 SGR 提取的 “理据” 是否与真实理据（Spurious-Motif 中已知的 motif 子图）更吻合。

实验设计

1. 数据集：Spurious-Motif（含真实理据标注）。

2. 指标：Precision@5（Top-5 预测理据与真实理据的重合度）。

3. 对比对象：所有基线模型。

实验结果

• SGR 在所有 Spurious-Motif 变体中，Precision@5 均高于其他基线（图 4 (a)(b)）。

• 无论捷径强度如何变化（$b=0.5$到 Cycle-Tree），SGR 的理据识别准确率始终领先。

结论

  SGR 能更精准地识别与标签有真实因果关系的理据，有效过滤捷径信息，验证了其 “理据提取准确性” 的核心优势。

实验 4：消融实验（验证模型组件必要性）

实验目标

  验证 SGR 核心组件（捷径引导器、Ldiff​、环境模块Le​）的必要性。

实验设计

1. 数据集：OGBG（GIN 作为 backbone）。

2. 消融变体：

   • SGR w/o shortcut：移除捷径引导器（剔除Lshortcut​）；

   • SGR w/o diff：移除跨环境稳定性损失（剔除Ldiff​）；

   • SGR w/o env：移除环境模块（剔除Le​+Ldiff​）。

3. 指标：ROC-AUC。

实验结果

消融变体	性能变化
SGR w/o shortcut	性能显著下降，与 CAL 等基线接近（验证捷径引导器的核心作用）。
SGR w/o diff	性能下降（如 MolHIV 下降 0.99%）（验证跨环境稳定性约束的必要性）。
SGR w/o env	性能优于部分基线，但仍低于原始 SGR（验证 “非理据作为环境” 的有效性）。

结论

• 捷径引导器是 SGR 性能提升的关键，证明 “从捷径中学习” 的核心思路有效。

• 跨环境稳定性损失（Ldiff​）与环境模块（Le​）能进一步提升理据的不变性与可靠性，是重要补充。

实验 5：可视化分析（理据识别直观性）

实验目标

  从定性角度验证 SGR 提取的理据是否合理、可解释。

实验设计

1. 数据集：Cycle-Tree（Spurious-Motif）、Graph-SST2。

2. 可视化对象：理据节点 / 边（红色边、藏青色节点）。

实验结果

数据集	具体结果
Cycle-Tree（House motif 测试例）	- SGR：准确识别 House motif 的核心节点 / 边，未包含 Tree/Wheel 等 base 子图（捷径载体）； - 基线（DIR/GSAT/GREA）：误将部分 base 子图节点 / 边纳入理据，识别精度较低（图 6）。
Graph-SST2（情感分析）	- 训练集：准确高亮 “quite effective”（正面）、“astonishingly witless”（负面）等情感关键词； - 测试集（OOD）：仍能精准识别核心情感词，解释与标签一致（图 9）。

结论

  SGR 提取的理据具有强直观性与可解释性，能精准定位与任务相关的核心结构，进一步验证了方法的有效性。

3.4 实验总结

1. 核心假设验证：GNN 优先学习捷径，训练初期模型可有效捕获捷径，为 SGR 提供理论支撑。

2. 性能优势：SGR 在 “任务预测准确性”“理据识别准确性” 上均显著优于经典 GNN 与主流基线。

3. 组件必要性：捷径引导器、跨环境稳定性损失、环境模块是 SGR 性能的关键保障。

4. 泛化能力：SGR 在合成、文本、分子等多场景数据集上均表现优异，验证了其广泛适用性。

 

 

相关问题

Q1：本文是如何验证 训练少量 epoch 的 $G_s$ 学习到的是捷径特征？

• • 验证思路：若$G_s$ 学到的是捷径，则它会呈现 “同分布准、OOD 差” 的恶性偏置行为；若学到的是理据，则会呈现 “跨分布稳定” 的泛化行为。

  • 具体验证实验与结果

  • 实验 1：$G_s$ 在偏置 / 无偏测试集上的性能差异

    • 实验设计：

1. • • 1. 数据集：Spurious-Motif（含偏置训练集，$b=0.5/0.7/0.9$ ，捷径强度递增；偏置测试集与训练集捷径一致，无偏测试集无捷径）。

       2. 模型：$G_s$ （GCN/GIN 为编码器，仅训练 2-3 个 epoch）。

       3. 指标：偏置 / 无偏测试集的准确率（ACC）。

     • 实验结果：

       • 偏置测试集：$G_s$ 准确率接近 100%（充分利用捷径拟合标签）。

       • 无偏测试集：$G_s$ 准确率显著下降（$b=0.9$ 时仅 35%-38%），且b越大（捷径越强），无偏测试集性能越差。

     • 结论：$G_s$ 依赖捷径而非真实理据进行预测，证明其学到的是捷径特征。

   • 实验 2：$G_s$ 在偏置 / 平衡数据上的训练速度差异

     • 实验设计：

1. • • 1. 数据集：Cycle-Tree（Spurious-Motif 变体，含 “偏置数据”（Cycle+Tree，捷径）和 “平衡数据”（Cycle+Tree/Wheel/Ladder，无捷径））。

       2. 模型：$G_s$ （仅训练少量 epoch）。

       3. 指标：训练损失、训练准确率的收敛速度。

     • 实验结果：

       • 偏置数据：训练 2 个 epoch 后，损失趋近于 0，准确率快速达到高值（捷径特征快速习得）。

       • 平衡数据：训练多个 epoch 后，损失才逐渐收敛，准确率提升缓慢（理据特征难学习）。

     • 结论：$G_s$ 在训练初期优先捕获易学习的捷径特征，而非难学习的理据特征。

   • 实验 3：$G_s$ 的 epoch 数与下游 SGR 性能的相关性

     • 实验设计：

       • 数据集：真实数据集 MolBACE（无显式捷径标注，通过下游性能反推$G_s$ 是否捕获捷径）。

       • 变量：$G_s$ 的训练 epoch 数（1-10 个）。

       • 指标：SGR 的下游任务性能（ROC-AUC）—— 若$G_s$ 捕获捷径，则 SGR 性能最优；若$G_s$ 开始学习理据，则 SGR 性能下降。

     • 实验结果：

• • • • epoch=1-3 时：SGR 性能随 epoch 增加而提升（$G_s$ 逐步捕获更多捷径特征）。

      • epoch>3 时：SGR 性能开始下降（$G_s$ 不再专注于捷径，转而学习理据特征，偏离 “捷径引导器” 的设计目标）。

    • 结论：仅训练少量 epoch（2-3 个）的$G_s$ 能精准捕获捷径特征，是下游 SGR 性能提升的关键；若训练过久，$G_s$ 会 “偏离捷径”，导致 SGR 去偏效果下降。

Q2：若数据中捷径特征与理据特征难以通过 “早停策略” 分离（如部分捷径特征学习难度接近理据特征），SGR 的捷径引导器$G_s$会捕获混杂信息，此时该如何调整$G_s$的训练策略（如早停 epoch 数、损失函数）以保证$h_s$的 “纯净捷径属性”？

Q3：在第二阶段优化中，$\mathcal{L}_{shortcut}$（互信息双向约束）与$\mathcal{L}_{sp}$（理据稀疏性约束）可能存在冲突（如过度追求稀疏性导致理据丢失关键信息，或过度剔除捷径导致理据不完整），该如何平衡两者的权重参数或优化逻辑？

Q4：当数据集无显式捷径标注（如多数真实场景），且不同样本的捷径强度差异较大时，SGR 如何自适应调整$G_s$的早停时机与$\mathcal{L}_{shortcut}$的约束强度，确保对不同样本的捷径捕获与理据分离效果一致？