RGDA——Rationalizing Graph Neural Networks with Data Augmentation【利用数据增强对图神经网络进行合理化解释】

论文信息

论文标题：Rationalizing Graph Neural Networks with Data Augmentation
论文作者：Gang Liu、Eric Inae、Tengfei Luo、Meng Jiang
论文来源：
论文地址：link
论文代码：link

Method

  

 

  

4.1 关键内容拆解

1. 符号简化：为统一节点级与图级任务的表述，将节点标签 $y_v$  与图标签 $y_g$  统一记为 $y$  ，用  $y_i/y_j$  表示索引为 $i/j$  的节点或图的标签，降低后续公式与逻辑的复杂度。

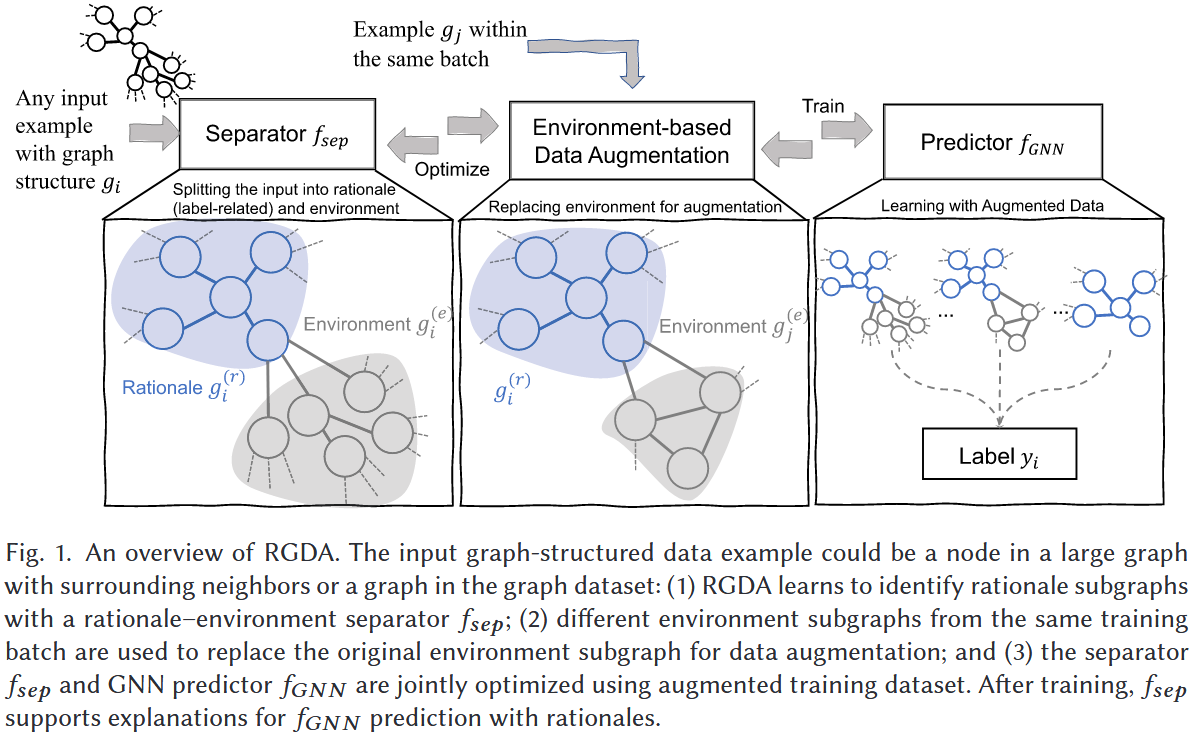
2. 核心思想：无论节点级还是图级任务，GNN 的预测均依赖 “计算图”（节点级为邻域图，图级为输入图本身）提取表征。RGDA 的统一逻辑是：

   • 在表征空间（而非显式图结构空间）中完成 “理据 - 环境分离”，避免图编解码的高复杂度；

   • 通过 “理据 - 环境组合” 生成增强样本，同时优化分离函数 $f_{sep}$  与 GNN 预测器 $f_{GNN}$  ，确保理据子图的准确性与模型泛化能力。

4.2 核心操作 1：理据 - 环境分离（Rationale-Environment Separation）

  通过分离函数 $f_{sep}$  将计算图划分为 “理据子图”（决定标签的核心结构）与 “环境子图”（无关噪声结构），针对节点级与图级任务设计差异化实现方式，但均基于表征空间操作。

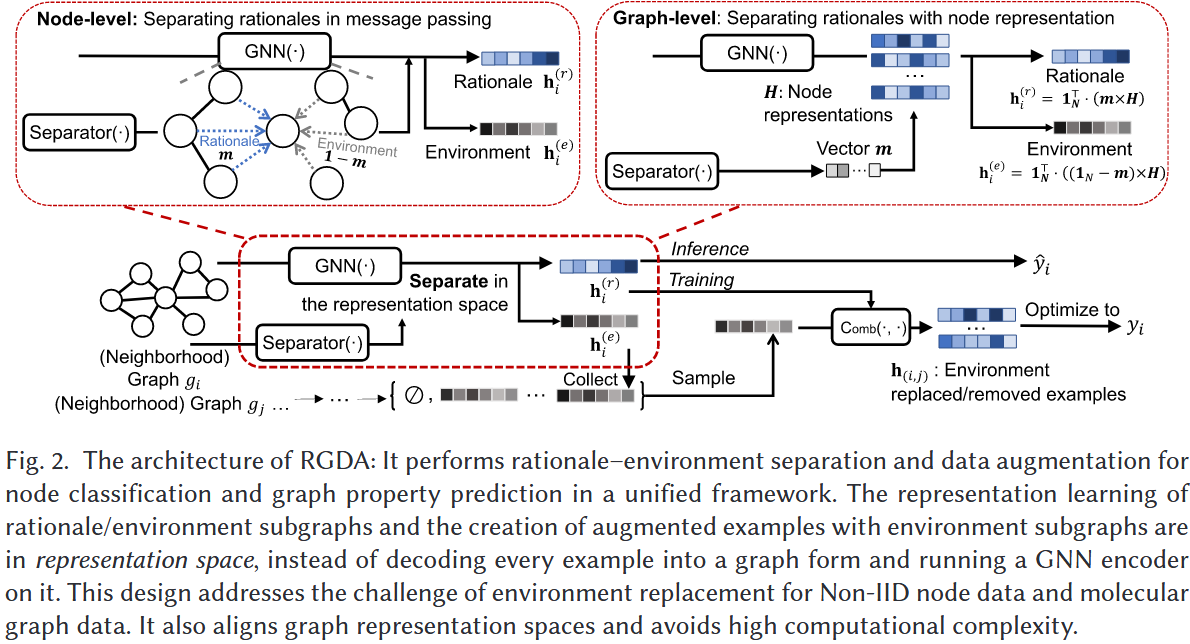
1. 节点分类任务的分离逻辑

适用场景：预测节点 $v$  的标签时，GNN 依赖其 $K$  阶邻居构成的 “隐式邻域图”，需从邻居中区分理据节点与环境节点。

关键步骤：

• Step 1：生成分离掩码：对节点 $v$  的每个直接邻居 $u$   ，通过多层感知机（MLP）计算掩码概率 $m_{vu}$  ，表示 $u$ 属于 $v$  的理据邻居的概率： 

    $m_{vu}=sigmoid\left(MLP_{sep }\left(\left[x_{v} \| x_{u}\right]\right)\right)$  

    其中 $[x_v \| x_u]$  表示节点 $v$  与 $u$  的特征向量拼接， $1-m_{vu}$  则为 $u$  属于环境邻居的概率。

• Step 2：理据子图表征计算：在 GNN 的 K 层消息传递中，仅传递理据邻居的加权消息（权重为 $m_{vu}$  ），更新理据子图的节点表征 $h_{v,k}^{(r)}$  ：

    $\begin{array} {rl}&{h_{v, k}^{(r)}=U_{k}\left( h_{v, k}^{(r)}, a_{v, k}^{(r)}\right) , where }\\ &{a_{v, k}^{(r)}=M_{k}\left( \left\{ \left( h_{v, k-1}^{(r)},h_{u, k-1}^{(r)},m_{v u}\right) , \forall u \in \mathcal {N}(v)\right\} \right) .}\end{array}$  

    初始理据表征 $h_{v,0}^{(r)}$ 由节点 $v$ 的原始特征 $x_v$ 初始化。

• Step 3：环境子图表征计算：仅在 GNN 第一层消息传递中使用 $1-m_{vu}$ 加权环境邻居消息，得到初始环境表征 $h_{v,1}^{(e)}$ ，后续 $K-1$ 层采用标准消息传递更新，最终得到环境子图表征 $h^{(e)}$ ：

      $\begin{array} {rl}&{h_{v,1}^{(e)}=U_{1}\left( x_{v},a_{v,1}^{(e)}\right) , where }\\ &{a_{v,1}^{(e)}=M_{1}\left( \left\{ (x_{v},x_{u},1-m_{vu}\right) ,\forall u\in \mathcal {N}(v)\right\} ).}\end{array}$

2. 图属性预测任务的分离逻辑

适用场景：预测整个图的属性（分类 / 回归）时，需从输入图的所有节点中区分理据节点与环境节点。

关键步骤：

• Step 1：生成节点级分离掩码：先通过专用 GNN（ $GNN_{sep}$ ）提取图中每个节点的上下文表征，再用 MLP 计算每个节点属于理据子图的概率 $m_v$ （掩码向量 $m$ ）：

            $m=sigmoid\left(MLP_{sep }\left(GNN_{sep }(g)\right)\right)$

            $1_N - m$ （ $1_N$ 为全 1 列向量）则为节点属于环境子图的概率。

• Step 2：生成 GNN 节点表征：用预测任务的 GNN（ $f_{GNN}$ ）提取全图节点的表征矩阵 $H=GNN(g)$

• Step 3：理据 / 环境子图表征计算：通过求和池化（readout 函数），分别对理据节点与环境节点的表征加权求和，得到两类子图的最终表征（维度 $\mathbb{R}^d$ ）：

              $h^{(r)}=1_{N}^{\top} \cdot(m \times H), \quad h^{(e)}=1_{N}^{\top} \cdot\left(\left(1_{N}-m\right) \times H\right)$

4.3 核心操作 2：基于环境子图的数据增强

  针对训练数据稀疏问题，利用分离得到的理据子图（ $h^{(r)}$ ）与环境子图（ $h^{(e)}$ ）表征，在表征空间中生成新训练样本，无需显式修改图结构，兼顾效率与有效性。

1. 增强操作的前提假设

  理据子图是决定标签的 “因果因子”，环境子图仅为 “噪声”，因此：

• • 仅用理据子图应能实现有效预测；

  • 替换环境子图不会改变标签，可用于生成多样化样本。

2. 两种核心增强策略

1）环境移除增强（Environment Removal Augmentation）

  目的：验证理据子图的预测有效性，强制模型依赖核心结构而非噪声。

  操作逻辑：仅使用理据子图表征 $h_i^{(r)}$ 进行预测，无需结合环境子图。

• • 节点分类：对 $h_i^{(r)}$ 应用 $softmax$  函数得到预测标签 $\hat{y}_i^{(r)}$ ；

  • 图属性预测：修改图预测公式，直接用 $h_i^{(r)}$ 输入 MLP 得到预测：

      $\hat{y}_{i}^{(r)}=MLP\left(h_{i}^{(r)}\right)$

2）环境替换增强（Environment Replacement Augmentation）

  目的：生成大量虚拟样本，增强模型对环境噪声的鲁棒性，缓解数据稀疏。

  操作逻辑：对批次内（共 $B$ 个样本）索引为 $i$ 的样本，将其理据子图表征 $h_i^{(r)}$ 与其他任意样本 $j$ （ $j \ne i$ ）的环境子图表征 $h_j^{(e)}$ 通过组合函数（Comb (・,・)）  拼接，生成新样本的表征 $h_{(i,j)}$ ，新样本标签仍为 $y_i$ （因理据子图未变）。

• • 1、组合函数选择：支持求和、均值、最大值、拼接等池化操作，论文默认使用元素级求和（实验验证效果最优）：

      $h_{(i,j)}=Comb\left(g_{i}^{(r)}, g_{j}^{(e)}\right)=h_{i}^{(r)}+h_{j}^{(e)}$

• • 2、预测逻辑：新样本的预测标签通过 MLP 计算：

            $\hat{y}_{(i,j)}=MLP\left(h_{(i,j)}\right)$

• • 3、样本数量控制：图级任务中，每个样本可与批次内 $\tilde{B}=B-1$ 个其他样本组合；节点级任务中， $\tilde{B}$ 设为超参数（避免样本量过大）。

4.4 模型优化：损失函数与训练策略

1. 损失函数设计

  根据任务类型（分类 / 回归）选择基础损失，结合增强样本损失与正则化损失，确保模型性能与理据子图质量。

  环境移除损失（ $\mathcal{L}_{rem}$ ）：确保理据子图单独预测的准确性

    二分类任务用交叉熵损失

    $\mathcal{L}_{rem}=y_i \cdot log \hat{y}_i^{(r)}+(1-y_i) \cdot log (1-\hat{y}_i^{(r)})$  

  环境替换损失（ $\mathcal{L}_{rep}$ ）：确保模型对环境噪声的鲁棒性

    批次内所有替换样本的平均交叉熵损失

    $\mathcal{L}_{rep}=\frac{1}{B}\sum_{j=1}^B [y_i \cdot log \hat{y}_{(i,j)}+(1-y_i) \cdot log (1-\hat{y}_{(i,j)})]$  

  正则化损失（ $\mathcal{L}_{reg}$ ）：避免理据子图过大（包含噪声）或过小（丢失关键结构）

    $\mathcal{L}_{reg }=\left|\frac{1}{N} \cdot 1_{N}^{\top} \cdot m-\gamma\right|$ ， $\gamma \in [0,1]$  

2. 训练策略：交替优化

  采用 “交替训练” 模式，分别优化分离函数 $f_{sep}$ 与 GNN 预测器 $f_{GNN}$ ，避免联合训练时的优化不稳定：

  预测器损失（  $\mathcal{L}_{pred}$  ） ：用于训练 $f_{GNN}$ ，仅包含增强样本的预测损失：

    $\mathcal{L}_{pred }=\mathcal{L}_{rem }+\alpha \cdot \mathcal{L}_{rep}$  

    其中 $\alpha$ 为超参数，控制替换损失的权重。

  分离函数损失（  $\mathcal{L}_{sep}$  ） ：用于训练 $f_{sep}$ ，额外加入正则化损失：

    $\mathcal{L}_{sep }=\mathcal{L}_{rem }+\alpha \cdot \mathcal{L}_{rep }+\beta \cdot \mathcal{L}_{reg }$  

    其中 $\beta$ 为超参数，控制正则化损失的权重。

  训练流程：迭代固定轮次 $T_{sep}$ （训练 $f_{sep}$ ）与 $T_{pred}$ （训练 $f_{GNN}$ ），直至模型收敛。

3. 推理阶段逻辑

  训练完成后，仅使用理据子图表征 $h_i^{(r)}$  进行最终预测（ $\hat{y}_i^{(r)}=MLP(h_i^{(r)})$ ），确保预测结果由核心理据支撑，提升可解释性。

4.5 复杂度分析：效率优势验证

  从时间复杂度角度，验证 RGDA 在大规模数据上的适用性，核心结论是 “表征空间操作显著降低复杂度”。

1. 基础复杂度（GNN 部分）

  假设单批次有 $n$ 个节点、 $m$ 条边，GNN 共 $K$ 层：

  单 GNN 层时间复杂度： $O(n d^2 + m d)$ （ $d$ 为表征维度，稀疏矩阵乘法优化）；

  $K$ 层 GNN 总复杂度： $O(K n d^2 + K m d)$ 。

2. RGDA 额外复杂度

  分离函数 $f_{sep}$ ：基于独立 GNN 实现，复杂度与标准 GNN 线性相关，无额外负担；

  数据增强操作：

    节点级任务：表征组合的复杂度为 $O(n^2)$ （ $n$ 为节点数）；

    图级任务：表征组合的复杂度为 $O(n'^2)$ （ $n'$ 为图数）；

总复杂度：

  节点级： $O(K n d^2 + K m d + n^2)$ ；

  图级： $O(K n d^2 + K m d + n'^2)$ 。

3. 效率优势

  相较于显式修改图结构的方法（如 DIR 需编解码子图，复杂度指数级增长），RGDA 在表征空间操作，复杂度仅线性增加，可支持大规模数据集（如 ogbn-Arxiv，百万级节点）。