[KTO] KTO: Model Alignment as Prospect Theoretic Optimization

论文信息

论文标题：KTO: Model Alignment as Prospect Theoretic Optimization
论文作者：卡温·埃萨亚拉杰、温妮·徐、尼克拉斯·米尼霍夫、丹·朱拉夫斯基、杜韦·基拉
论文来源：ICML 2024
论文地址：link
论文代码：link

Abstract

核心背景：卡尼曼和特沃斯基的前景理论指出，人类对随机变量的感知存在偏见（如损失厌恶）。
现有发现：用于对齐大语言模型（LLMs）与人类反馈的目标（如 DPO）隐含这些偏见，其成功部分源于属于 “人类感知损失（HALOs）” 家族，优于交叉熵最小化，但归因于人类的效用函数与前景理论有差异。
新方法：基于卡尼曼 - 特沃斯基人类效用模型，提出直接最大化生成内容效用的 HALO（KTO），仅需输出是否合意的二元信号，在 10 亿到 300 亿参数规模上性能等同或超越基于偏好的方法。
结论：不存在普适最优的 HALO，最佳损失函数取决于特定场景下最合适的归纳偏差，这是常被忽视的点。

典型例子：损失厌恶（Loss Aversion）

损失厌恶是这类偏见中最著名的一种，由卡尼曼和特沃斯基通过实验发现，指人们对损失的痛苦感受，远大于对同等收益的快乐感受。

实验案例：　　
若有一个赌局：50% 概率赢 100 元，50% 概率输 100 元。从理性角度看，预期收益为 0（100×50% + (-100)×50% = 0），但大多数人会拒绝这个赌局 —— 因为 “输 100 元的痛苦” 比 “赢 100 元的快乐” 更强烈。
研究发现，这种 “痛苦” 的强度通常是 “快乐” 的 2-3 倍。
生活中的体现：
- 投资者不愿卖出亏损的股票（“只要没卖就不算亏”），哪怕继续持有会损失更多；
- 消费者丢失 100 元的难过，比捡到 100 元的开心更持久；
- 员工对 “工资减少 10%” 的抵触，远大于对 “工资增加 10%” 的满足。

2 Background

1. 预训练（Pretraining）

　　给定大规模语料库，训练模型以最大化 “基于前文预测下一个 token” 的对数概率。用 $\pi_0$ 表示预训练模型。

　　　　$\max_{\pi_0} \mathbb{E} \left[ \sum_{t} \log \pi_0(x_t \mid x_1, x_2, \ldots, x_{t-1}) \right]$

　　其中，$x_1, x_2, \ldots, x_t$ 表示语料库中的 token 序列，$\pi_0(x_t \mid x_1, \ldots, x_{t-1})$ 是预训练模型基于前文序列预测下一个 token $x_t$ 的概率，整个公式的目标是最大化该概率的对数之和的期望。

2. 有监督微调（Supervised Finetuning, SFT）

　　在与下游任务更相关的数据上微调模型，使其更精准地预测下一个token。这类数据通常包含指令及对应的合适响应（即“指令微调”）。用 $\pi_{ref}$ 表示微调后的模型。

3. 基于人类反馈的强化学习（RLHF）

　　给定偏好数据集 $D = \{(x, y_w, y_l)\} $（其中 $x$ 为输入， $y_w $ 和 $y_l $ 分别为偏好和非偏好输出，即 $y_w \succ y_l $ ），假设存在“真实奖励函数” $r^* $，则 $y_w$ 优于 $y_l $ 的概率可通过特定函数类（通常是Bradley-Terry 模型）建模，其中 $\sigma $ 为逻辑函数：

　　　　$p^*(y_w \succ y_l | x) = \sigma(r^*(x, y_w) - r^*(x, y_l)) \quad (1)$

　　由于直接获取人类的真实奖励成本极高，需训练奖励模型 $r_\phi $ 作为替代，通过最小化人类偏好数据的负对数似然实现：

　　　　$\mathcal{L}_R(r_\phi) = \mathbb{E}_{x, y_w, y_l \sim D} \left[ -\log \sigma(r_\phi(x, y_w) - r_\phi(x, y_l)) \right]$

　　但仅最大化奖励可能牺牲生成文本的语法正确性等特性。为避免此问题，引入 KL 散度惩罚项，限制模型与 $\pi_{ref} $ 的偏离程度。设 $\pi_\theta $ 为待优化模型，最优模型 $\pi^* $ 需最大化：

　　　　$\mathbb{E}_{x \in D, y \in \pi_\theta} \left[ r_\phi(x, y) \right] - \beta D_{KL}(\pi_\theta(y|x) \| \pi_{ref}(y|x)) \quad (2)$

　　其中 $\beta > 0 $ 为超参数。由于该目标不可微，需使用 PPO 等强化学习算法（Schulman 等人，2017）。

　　然而，RLHF通常速度慢（主要因需采样生成结果）且实践中不稳定（尤其在分布式场景）。因此，近年研究聚焦于设计闭形式损失函数，直接最大化偏好与非偏好输出的间隔。其中，直接偏好优化（DPO，Rafailov 等人，2023）成为热门替代方法，在特定条件下可复现 RLHF 的最优策略：

　　　　$\mathcal{L}_{DPO}(\pi_\theta, \pi_{ref}) = \mathbb{E}_{x, y_w, y_l \sim D} \left[ -\log \sigma\left( \beta \log \frac{\pi_\theta(y_w|x)}{\pi_{ref}(y_w|x)} - \beta \log \frac{\pi_\theta(y_l|x)}{\pi_{ref}(y_l|x)} \right) \right] \quad (3)$

3 A Prospect Theoretic View of Alignment

定义 3.1 价值函数：价值函数 $v: Z \to \mathbb{R}$ 将结果 $z$ （相对于某个参考点 $z_0$ ）映射到其感知（或主观）价值。例如，这类函数可捕捉人类的一个特性：对同等幅度的相对损失比相对收益更敏感（即损失厌恶）。
定义 3.2 权重函数：权重函数 $\omega$ 是“容量函数”的导数，用于将累积概率转换为人类感知的累积概率。例如，它可捕捉人类倾向于高估罕见事件发生概率的特性， $\omega_z$ 表示赋予结果 $z$ 的权重。
定义 3.3 随机变量的效用：随机变量 $Z$ 的效用是其所有结果的函数： $u(Z) \triangleq \sum_{z \in Z} \omega_z v(z - z_0)$ ，即通过权重函数 $\omega_z$ 对各结果的价值 $v(z - z_0)$ 加权求和得到总效用。

　　由于人类无法观测到大语言模型（LLM）的完整概率分布，权重函数在此处的讨论中不突出，因此重点分析价值函数。

　　Tversky & Kahneman（1992）提出的人类价值函数：

　　　　$v\left(z ; \lambda, \alpha, z_0\right)= \begin{cases}\left(z-z_0\right)^{\alpha} & \text { if } z \geq z_0 \quad \text {（收益）} \\ -\lambda\left(z_0-z\right)^{\alpha} & \text { if } z<z_0 \quad \text {（损失）}\end{cases} \tag{4}$

　　　　参数含义：

- - $\alpha = 0.88$：控制函数曲率，反映风险厌恶程度（ $\alpha < 1$ 时，收益区域为凹函数，体现“边际收益递减”）
  - $\lambda = 2.25$ ：控制函数斜率，反映损失厌恶程度（ $\lambda > 1$ 意味着同等损失比收益带来更强的主观感受）

　　　　关键特性：

- - 参考点依赖：价值基于相对于 $z_0$ 的收益或损失，而非绝对量；
  - 收益凹性：收益区域（ $z \geq z_0$ ）为凹函数，即随着收益增加，主观价值的增速放缓（敏感性递减）；
  - 损失厌恶：损失区域（ $z < z_0$ ）的斜率更陡，即同等损失比收益对主观价值的影响更大；
  - 个体差异：该函数的形状存在个体差异（如图1所示的中位数曲线），后续研究也提出了其他形式（如Gurevich等人，2009）；

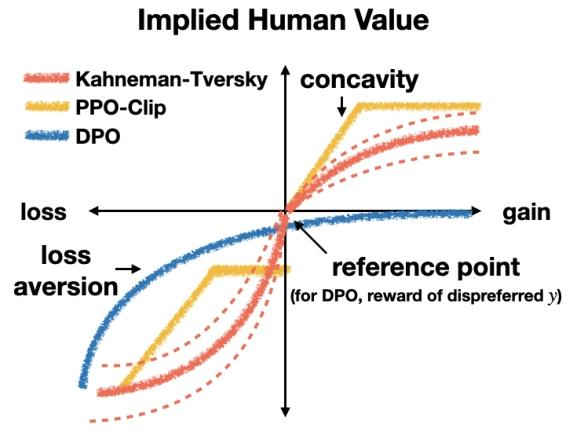
　　核心坐标轴与概念

- 横轴（gain/loss）：表示模型输出与 “参考点” 的相对关系纵轴：表示“隐含的人类价值（Implied Human Value）”，即不同方法对输出结果的主观价值判断强度；
  - 右侧“gain（收益）”：输出优于参考点（如更符合人类偏好）；
  - 左侧“loss（损失）”：输出差于参考点（如违背人类偏好）；

　　Kahneman-Tversky（红色虚线）

- 理论基础：基于前景理论（Prospect Theory），是心理学中描述人类真实决策偏好的经典模型。
- 曲线特征：关键意义：代表 “真实人类决策” 的价值倾向，是心理学实证研究的总结；
  - 收益端（右侧）：呈凹性（concavity）——随着收益增加，价值增速逐渐放缓（反映“风险厌恶”：对额外收益的敏感度递减）；
  - 损失端（左侧）：斜率更陡且呈凸性——同等损失比收益带来更强的负向价值（反映“损失厌恶（loss aversion）”：人类对损失的痛苦感受远大于收益的快乐）。

　　DPO（蓝色实线）

- 方法背景：直接偏好优化（Direct Preference Optimization），用 “偏好对” 替代奖励模型的简化对齐方法；
- 曲线特征：关键意义：体现 DPO 对 “偏好差异” 的线性化、弱敏感倾向，更关注 “相对偏好” 而非极端损失;
  - 参考点特殊：参考点定义为“非偏好输出的奖励（reward of dispreferred $y$ ）”，即把“差输出”作为基准；
  - 收益端（右侧）：价值随收益增加缓慢上升（对“更优输出”的敏感度低）；
  - 损失端（左侧）：斜率相对平缓（对“更差输出”的惩罚不极端）;

人类感知损失（HALOs，Human - Aligned Losses）

　　HALOs 定义：

- $ \theta $：待对齐模型 $ \pi_\theta: X \to \mathcal{P}(Y) $（从输入 $ X $ 到输出分布 $ \mathcal{P}(Y) $）的可训练参数。
- $ \pi_{ref} $：参考模型（如 SFT 后的基线模型）；
- $ l: Y \to \mathbb{R}^+ $：归一化因子（平衡不同输出 $ y $ 的权重，避免偏差）；
- $ r_\theta(x, y) = l(y) \cdot \log \left( \large {\frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)} } \right) $：隐含奖励——通过对比待对齐模型与参考模型的输出概率比，衡量 $ (x, y) $ 的相对优劣（概率比越大，奖励越高）；

　　人类价值的构建逻辑

- $ Q(Y' | x) $：输入 $ x $ 下，输出 $ y' $ 的参考点分布（可理解为“基准预期”，比如基于参考模型的典型输出分布）。
- $ v: \mathbb{R} \to \mathbb{R} $：价值函数，需满足两个条件：
  - 全局非递减（收益越高，价值越高；损失越高，价值越低）；
  - 收益端（$ (0, \infty) $ 区间）为凹函数（反映“风险厌恶”：额外收益的价值增速随收益增大而放缓）。

　　最终，人类对 $ (x, y) $ 的价值定义为：

　　　　$v\left( r_\theta(x, y) \;-\; \mathbb{E}_{Q} \left[ r_\theta(x, y') \right] \right)$

　　即：用 “当前输出 $ y $ 的隐含奖励 ”减去“ 参考点分布下的期望奖励”，再通过价值函数 $ v $ 映射为最终的“人类感知价值”。

　　人类感知损失（human-aware loss）：

　　　　$\begin{aligned} f\left(\pi_{\theta}, \pi_{\text{ref}}\right)= \mathbb{E}_{x, y \sim \mathcal{D}}\left[a_{x, y} \, v\left(r_{\theta}(x, y) - \mathbb{E}_{Q}\left[r_{\theta}\left(x, y'\right)\right]\right)\right] + C_{\mathcal{D}} \end{aligned}$

　　　　符号介绍：

- - $f(\pi_\theta, \pi_{ref}) $：损失函数，衡量待对齐模型 $\pi_\theta $ 与参考模型 $\pi_{ref} $ 的“对齐差距”；
  - $a_{x,y} \in \{-1, +1\} $：反馈符号，表示人类对 $(x,y) $ 的偏好方向（$+1 $ 为合意输出，$-1 $ 为不合意输出）；
  - $v(\cdot) $：价值函数（呼应前文 Kahneman-Tversky 价值函数或其变体，反映人类对收益/损失的主观价值）；
  - $r_\theta(x,y) $：隐含奖励（由模型输出概率比定义，$r_\theta(x,y) = l(y) \cdot \log \frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)} $ ）；
  - $\mathbb{E}_Q[r_\theta(x,y')] $：参考点分布 $Q $ 下的“基准奖励”（衡量模型输出的相对收益/损失）；
  - $\mathcal{D} $：反馈数据集（含人类对模型输出的偏好标注），$C_\mathcal{D} $ 是与数据相关的常数（不影响优化方向，仅调整整体偏移）；

4. Kahneman-Tversky Optimization

　　经典的 Kahneman-Tversky 价值函数（公式4）形式为：

　　　　$v(z; \lambda, \alpha, z_0) = \begin{cases} (z-z_0)^\alpha & \text{if } z \geq z_0 \\ -\lambda(z_0-z)^\alpha & \text{if } z < z_0 \end{cases}$

　　但该函数因指数项 $\alpha$ 在优化过程中易导致数值不稳定（如极端值放大）。因此，KTO 改用逻辑函数 $\sigma(\cdot)$ 替代，原因是：

- 逻辑函数在收益端（正向偏差）呈凹性，损失端（负向偏差）呈凸性，与前景理论中人类对收益/损失的主观感知特性一致；
- 数值特性更稳定，避免了指数项带来的优化波动；

　　引入风险厌恶超参数$\beta$

- 作用：控制价值函数的饱和速度，直接调节模型的风险态度：$\beta$ 越大，逻辑函数 $\sigma(\beta \cdot \text{偏差})$ 饱和越快（即随偏差增大，价值增速放缓并趋于稳定）；
- 反映人类决策中的“风险厌恶”：对收益而言，$\beta$ 大意味着“额外收益的边际价值递减更快”（更保守）；对损失而言，意味着“损失的边际痛苦递减更快”（更敢承担风险）；
- 与 DPO 中 $\beta$ 的对比：DPO 的 $\beta$ 源于 RLHF 中的 KL 约束，用于限制模型与参考模型的偏离程度；而 KTO 的 $\beta$ 是显式用于控制风险态度的超参数，物理意义更明确；

　　用 $\lambda_D$ 和 $\lambda_U$ 替代单一损失厌恶系数 $\lambda$

　　经典前景理论中，$\lambda$（$\lambda>1$）控制损失厌恶程度（损失的痛苦＞同等收益的快乐）。

　　KTO 将其拆分为两个参数：

- $\lambda_D$：针对合意输出（desirable）的损失厌恶系数；
- $\lambda_U$：针对不合意输出（undesirable）的损失厌恶系数；

　　灵活性提升：可通过调整两者比例（如 $\lambda_U > \lambda_D$）强化对不合意输出的抑制，或适配数据不平衡场景（如少数合意样本需更高权重）。

　　参考点$z_0$的重新定义

DPO的参考点：以单个非偏好输出（$y_l$）为基准，仅关注“偏好对”的相对差异。
KTO的参考点：

　　　　认为人类判断输出质量时，会与“所有可能输出”比较，因此将参考点定义为KL散度：

　　　　$z_0 = D_{KL}(\pi_\theta(y'|x) \| \pi_{ref}(y'|x))$

　　即待对齐模型与参考模型的整体分布差异，更贴近人类“全局比较”的认知模式。

实际计算：因直接估计$z_0$需采样所有可能输出（计算昂贵），KTO采用有偏估计（如微批次内的不匹配样本对），在效率与准确性间权衡。

　　KTO损失函数的最终形式

　　　　$\mathcal{L}_{KTO}(\pi_\theta, \pi_{ref}) = \mathbb{E}_{x,y \sim \mathcal{D}} \left[ \lambda_y - v(x,y) \right]$

　　其中：

　　　　　　隐含奖励：

　　　　　　参考点：$z_0 = \text{KL}(\pi_\theta(y' \mid x) \parallel \pi_{\text{ref}}(y' \mid x))$

　　　　　　价值函数/效用函数：

　　　　　　　　$v(x, y) = \begin{cases} \lambda_D \sigma(\beta(r_\theta(x, y) - z_0)) & \text{if } y \sim y_{\text{desirable}} \mid x \\ \lambda_U \sigma(\beta(z_0 - r_\theta(x, y))) & \text{if } y \sim y_{\text{undesirable}} \mid x \end{cases}$

其中

- - - $\lambda_D$ 和 $\lambda_U$ 分别是对可取和不可取输出的权重，用于处理数据不平衡；
    - $r_\theta(x, y) = \log \frac{\pi_\theta(y \mid x)}{\pi_{\text{ref}}(y \mid x)}$ 是策略模型相对于参考模型的对数概率比；
    - $z_0 = \text{KL}(\pi_\theta(y' \mid x) \parallel \pi_{\text{ref}}(y' \mid x))$ 是参考点，通常设定为参考模型的期望奖励。

　　计算参考点 $z_0$

　　参考点 $z_0$

　　　　$\large z_0 = \mathbb{E}_{y' \sim \pi_{\text{ref}}(Y|x)}[r_\theta(x, y')]$

　　由于直接计算期望值较为复杂，KTO 采用 批次内不匹配对 的方法进行近似估计：

$\large \hat{z}_0 = \max\left(0, \frac{1}{m} \sum_{i=1}^m \log\frac{\pi_\theta(y_{j}|x_i)}{\pi_{\text{ref}}(y_{j}|x_i)}\right)$

其中，$m$ 是批次大小，$j=(i+1) mod m$ 表示在同一批次内循环配对不同的输入和输出。

计算效用值

根据输出 $y$ 的类型（可取或不可取），计算对应的效用值：

可取输出 $ $y_{w}$ ：

$\large v(x, y_w) = \lambda_D \cdot \sigma\left(\beta \cdot (r_\theta(x, y_w) - z_0)\right)$

不可取输出 $ $y_{w}$ ：

$v(x, y_l) = \lambda_U \cdot \sigma\left(\beta \cdot (z_0 - r_\theta(x, y_l))\right)$

总效用计算

结合可取和不可取输出的效用，定义总效用 $U(x, y_w, y_l)$

$U(x, y_w, y_l) = v(x, y_w) - v(x, y_l)$

损失函数设计

KTO 的损失函数旨在最大化生成内容的总效用，具体定义为：

$\mathcal{L}_{\text{KTO}} = -\log(\sigma(U(x, y_w, y_l)))$

替换总效用的表达式，可以进一步展开为：

$\mathcal{L}_{\text{KTO}} = -\log\left(\sigma\left(\lambda_D \cdot \sigma\left(\beta \cdot (r_\theta(x, y_w) - z_0)\right) - \lambda_U \cdot \sigma\left(\beta \cdot (z_0 - r_\theta(x, y_l))\right)\right)\right)$

Reference

https://inuyashayang.github.io/AIDIY/RLHF_Pages/KTO/

LLM中人类感知损失算法家族项目：https://github.com/ContextualAI/HALOs/tree/main

包含算法：DPO, KTO, PPO, ORPO

posted @ 2025-08-09 17:12 Blairs 阅读(270) 评论(0) 收藏举报

刷新页面返回顶部

xxai