数据集的划分
在机器学习算法中，我们通常将原始数据集划分为三个部分（划分要尽可能保持数据分布的一致性）：
（1）Training set（训练集）: 训练模型
（2）Validation set（验证集）： 选择模型
（3）Testing set（测试集）： 评估模型
其中Validation set的作用是用来避免过拟合的。在训练过程中，我们通常用它来确定一些超参数（例：根据Validation set的accuracy来确定early stoping的epoch大小，根据Validation set确定learning rate等等）。之所以不用Testing set，是因为随着训练的进行，网络会慢慢过拟合测试集，导致最后的Testing set没有参考意义。因此Training set用来计算梯度更新权重，即训练模型，Validation set用来做模型选择，Testing set则给出一个accuracy以判断网络性能的好坏。
数据集的划分通常有三种方法：
（1）留出法（Hold-out）
将数据集\(D\)划分为两个互斥的集合，其中一个集合作为训练集\(S\)，另一个集合作为测试集\(T\)，即\(D=S\cup T\)，\(S\cap T = \varnothing\)。在\(S\)上训练出模型后，用\(T\)来评估其误差。Andrew NG老师在《Deep learning》课程中对数据集的划分讲解如下：
（a）Previous era of machine learning。数据量为10000左右。如果只是划成训练集和测试集则为：70%验证集，30%测试集。如果划成训练集、验证集和测试集则为：60%训练集，20%验证集，20%测试集。
（b）Big data era：数据量为百万级别。 验证集和测试集占数据总量的比例会趋向变得更小。比如有1000000条数据，只需各拿出10000条作为验证集和测试集。
（2）交叉验证法（Cross Validation）
将数据集\(D\)划分为 \(k\) 个大小相似的互斥子集，即\(D=D_1\cup D_2 \cup \cdots \cup D_k\)，\(D_i \cap D_j = \varnothing（i \not = j）\)。每个子集都要尽可能保持数据分布的一致性，即从D中通过分层采样得到。然后用 \((k-1)\) 个子集的并集作为训练集，余下的子集作为测试集。这样就可以获得 \(k\) 组训练/测试集，从而可以进行 \(k\) 次训练和测试，最终返回的是 \(k\) 个测试结果的均值。交叉验证法评估结果的稳定性和保真性在很大程度上取决于 \(k\) 的取值。如10折交叉验证：
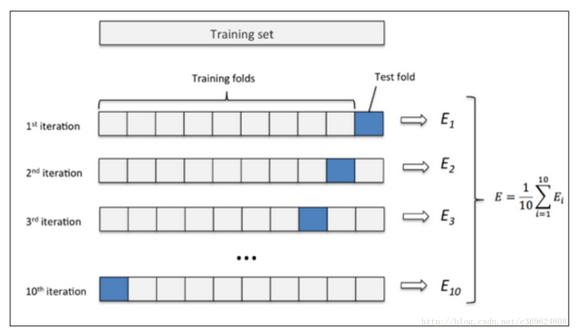
交叉验证法优点和缺点：
（a）优点：从有限的数据中尽可能挖掘多的信息，从各种角度去学习我们现有的有限的数据，避免出现局部的极值。在这个过程中无论是训练样本还是测试样本都得到了尽可能多的学习。
（b）缺点：当数据集比较大时，训练模型的开销较大。
（3）自助法（BootStrapping）
每次随机从初始数据集 \(D\) 中选择一个样本拷贝到结果数据集 \(D'\) 中，重复操作 \(m\) 次 ，就得到了含有 \(m\) 个样本的数据集 \(D'\) （注意：\(D\) 中有部分样本会在 \(D'\) 中多次出现）。将 \(D'\) 作为训练集，\(D\setminus D'\) 作为验证集（测试集）。样本在 \(m\) 次采样中始终不被采集到的概率是 \((1-\frac{1}{m})^m\) ，取极限为：
通过自助采样，初始数据集中约有36.8%的样本未出现在采样集 \(D'\) 中。
自助法优点和缺点：
（a）优点：自助法在数据集较小、难以有效划分训练集和测试集时很有用。此外，自助法能从初始数据集中产生多个不同的训练集，这对集成学习等方法有很大的好处。
（b）缺点：自助法产生的数据集改变了初始数据集的分布，这会引入估计偏差。因此在初始数据量足够时，留出法和交叉验证法更加常用一些。
Reference:
