洛谷P1149 火柴棒等式题解

P1149[NOIP2008 提高组] 火柴棒等式

题目描述

给你 \(n\) 根火柴棍，你可以拼出多少个形如 \(A+B=C\) 的等式？等式中的 \(A\)、\(B\)、\(C\) 是用火柴棍拼出的整数（若该数非零，则最高位不能是 \(0\)）。用火柴棍拼数字 \(0\sim9\) 的拼法如图所示：

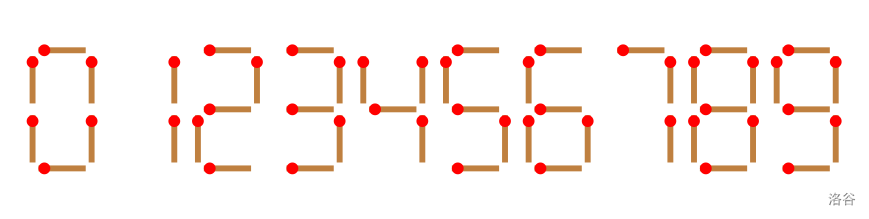
注意：

1. 加号与等号各自需要两根火柴棍；
2. 如果 \(A\neq B\)，则 \(A+B=C\) 与 \(B+A=C\) 视为不同的等式（\(A,B,C\geq0\)）；
3. \(n\) 根火柴棍必须全部用上。

输入格式

一个整数 \(n(1 \leq n\leq 24)\)。

输出格式

一个整数，能拼成的不同等式的数目。

样例 #1

样例输入 #1

14

样例输出 #1

2

样例 #2

样例输入 #2

18

样例输出 #2

9

提示

【输入输出样例 1 解释】

\(2\) 个等式为 \(0+1=1\) 和 \(1+0=1\)。

【输入输出样例 2 解释】

\(9\) 个等式为

\(0+4=4\)、\(0+11=11\)、\(1+10=11\)、\(2+2=4\)、\(2+7=9\)、\(4+0=4\)、\(7+2=9\)、\(10+1=11\)、\(11+0=11\)。

思路：

虽然这题标签是搜索，但是因为\(n\le24\)，所以只需要双重\(for\)循环就可以搞定，至于循环多少次~~
首先\(n\le24\)，加号和等于号用了\(4\)根，还剩20根，数字\(1\)需要两根，加数、加数、和平均一个数\(6\sim7\)根，也就是\(3\sim4\)个1，四位数，所以双重循环\(1000\times1000\)次。

代码：

#include<iostream>
using namespace std;
int a[10]={6,2,5,5,4,5,6,3,7,6},n,ans=0;//a数组表示0~9每个数字要用多少根火柴棒
int f(int x){//表示拼成数字x需要多少根火柴棒
	if(x==0){//特判x==0
		return 6;
	}
	int res=0;
	while(x){//数位提取
		res+=a[x%10];
		x/=10;
	}
	return res;
}
int main(){
	cin>>n;
	for(int i=0;i<=1000;i++){
		for(int j=0;j<=1000;j++){
			if(f(i)+f(j)+f(i+j)+4==n){//判断是否刚好用完
				ans+=1;//记录答案
			}
		}
	}
	cout<<ans;
	return 0;
}