leetcode 找到最终安全状态

 

 

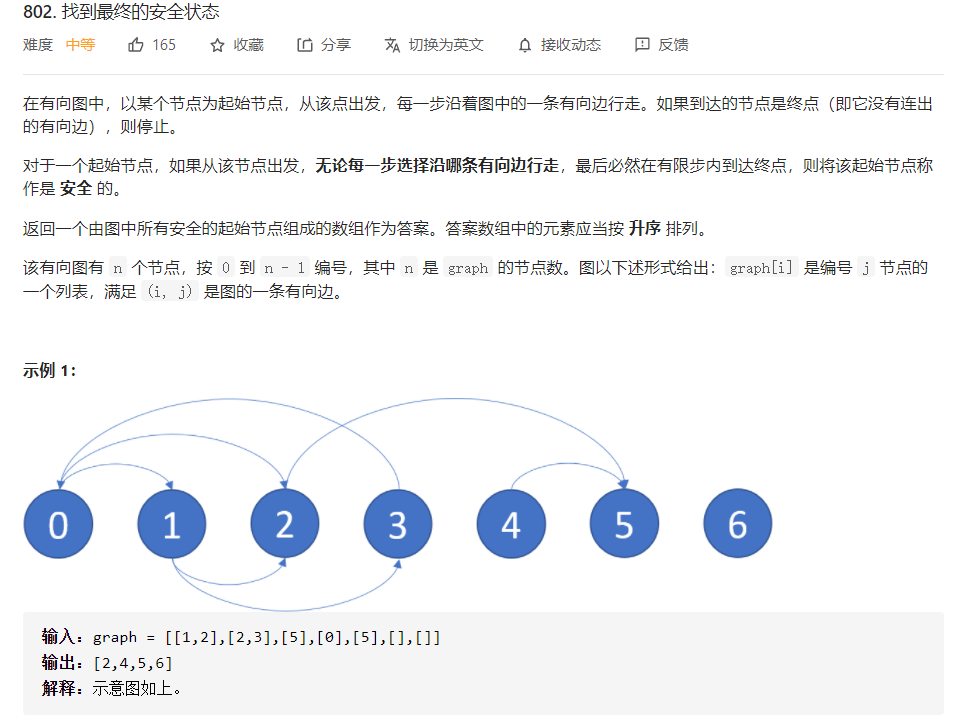
这道题最初我的想法是遍历+BFS但时间超了，所以在这里给一个官方的解答：

深度优先搜索 + 三色标记法
根据题意，若起始节点位于一个环内，或者能到达一个环，则该节点不是安全的。否则，该节点是安全的。

我们可以使用深度优先搜索来找环，并在深度优先搜索时，用三种颜色对节点进行标记，标记的规则如下：

白色（用 00 表示）：该节点尚未被访问；
灰色（用 11 表示）：该节点位于递归栈中，或者在某个环上；
黑色（用 22 表示）：该节点搜索完毕，是一个安全节点。
当我们首次访问一个节点时，将其标记为灰色，并继续搜索与其相连的节点。

如果在搜索过程中遇到了一个灰色节点，则说明找到了一个环，此时退出搜索，栈中的节点仍保持为灰色，这一做法可以将「找到了环」这一信息传递到栈中的所有节点上。

如果搜索过程中没有遇到灰色节点，则说明没有遇到环，那么递归返回前，我们将其标记由灰色改为黑色，即表示它是一个安全的节点。

链接：https://leetcode-cn.com/problems/find-eventual-safe-states/solution/zhao-dao-zui-zhong-de-an-quan-zhuang-tai-yzfz/

class Solution {
    public List<Integer> eventualSafeNodes(int[][] graph) {
        int n = graph.length;
        int[] color = new int[n];
        List<Integer> ans = new ArrayList<Integer>();
        for (int i = 0; i < n; ++i) {
            if (safe(graph, color, i)) {
                ans.add(i);
            }
        }
        return ans;
    }

    public boolean safe(int[][] graph, int[] color, int x) {
        if (color[x] > 0) {
            return color[x] == 2;
        }
        color[x] = 1;
        for (int y : graph[x]) {
            if (!safe(graph, color, y)) {
                return false;
            }
        }
        color[x] = 2;
        return true;
    }
}