[翻译转载] 离散数学教程--序+集合,关系和函数
Discrete Mathematics
简介
数学可以大致被分为两个分支
- 连续数学: 它基于连续的数轴或者实数. 特征是任意两数之间的数都是几乎无限个.例如,在连续数学中的方程可以被画成一条光滑不间断的曲线.
- 离散数学: 它包含了间断的值,即任意两个点之间总包含可数个点. 比如一个有限对象的集合的方程被定义为一系列包含这些对象的有序对,并且可以表示成这些对的列表.
离散数学所讨论的
尽管不能有一个确切的数字表示离散数学的分支,下面的方向几乎在所有研究中都被认为很重要
- 集合,关系和函数
- 数理逻辑
- 群论
- 计数理论
- 概率
- 数学归纳和递推关系
- 图论
- 树和森林
- 布尔代数
我们将会在这个教程的后序章节讨论这些概念.
集合
德国数学家G. Cantor引入了集合的概念. 他将集合定义为被确定的定义或规则所选中的一系列确定的,可辨识的对象.
集合论是其他几个领域如计数理论,关系,图论和有限状态机的基础.这个章节我们会涵盖集合论的不同方面
定义
一个集合由一系列无序的不同元素组成. 可以用集合括号显式得写出所有元素. 元素的顺序变化和重复并不会引起集合的变化.
集合的例子:
- 正整数集合
- 太阳系所有的植物
- 印度所有的邦
- 字母表中的小写字母
集合的表示
集合有两种表示方式
- 列举或表格
- 构造条件
列举或表格
将集合中所有的元素列举出来,将元素包裹在括号中,并以逗号分隔.
例1- 英语元音字母, \(A = \{ a,e,i,o,u \}\)
例2- 小于10的奇数, \(B = \{ 1,3,5,7,9 \}\)
构造条件
将集合表示成所有元素共同的性质 \(A = \{ x:p(x) \}\)
例1- 集合\(\{ a,e,i,o,u \}\) 可被写成 $$A = \lbrace x:x 是英语元音字母 \rbrace$$
例2- 集合\(\{ 1,3,5,7,9 \}\) 被写成 $$B = \lbrace x:1 \le x \lt 10 ; and (x \% 2) \ne 0\rbrace$$
元素x属于集合S记做\(x \in S\), 元素y不属于集合S记做\(y \notin S\)
例- 如果\(S = \{ 1,1.2,1.7,2 \}, 1 \in S 但 1.5 \notin S\)
一些重要的集合
- 自然数集合\(\mathbb{N} = \{1,2,3,4,\dots\dots \}\)
- 整数集合\(\mathbb{Z} = \{\dots,-3,-2,-1,0,1,2,3,\dots\}\)
- 正整数集合\(\mathbb{Z}'\)
- 有理数集合\(\mathbb{Q}\)
- 实数集合\(\mathbb{R}\)
- 全体数集\(\mathbb{W}\)
集合的基
集合S的基记做\(|S|\),是集合元素的个数,也被叫做集合的基数. 如果一个集合有无限多个元素,他的基是\(\infty\)
例: \(|{1,4,3,5}|=4,|{1,2,3,4,5,...}|=\infty\)
对于两个集合X和Y
- \(|X| = |Y|\) 表示两个集合的基相同,即两个集合元素个数相同,那么存在一个从X到Y的双射函数'f'
- \(|X| \le |Y|\) 表示X的基小于等于Y的基,即X的元素个数小于等于Y的元素个数. 存在一个X到Y的单射'f'
- \(|X| \lt |Y|\) 表示X的基小于Y的基,即X的元素个数小于Y的元素个数. X到Y的单射'f'一定不是双射
- \(|X| \le |Y| 和 |X| \ge |Y|同时成立即|X| = |Y|\) 集合X和Y通常被称作等价集合
集合的类型
集合可以分为许多种,如有限集,无限集,子集,真子集,全集等等.
有限集
集合中有确定个数个元素
例- \(S = \{x|x \in \mathbb{N} \ and \ 70 > x \gt 50\}\)
无穷集
集合有无线个元素
例- \(S = \{x|x \in \mathbb{N} \ and \ x > 10\}\)
子集
集合X是集合Y的子集(记做\(X \subseteq Y\))表示X中的所有元素都在Y中
例1- \(设 X=\{1,2,3,4,5,6\} 和 Y=\{1,2\}\),那么Y就是X的子集,可以写做\(Y \subseteq X\).
例2- \(设 X=\{1,2,3\} 和 Y=\{1,2,3\}\),那么因为Y中的所有元素都在X里,Y就是X的子集(不是真子集),写做\(Y \subseteq X\).
真子集
真子集表示是子集但不是本身.集合X是集合Y的真子集(写做\(X \subset Y\))要求X是Y的子集且\(|X| < |Y|\)
例- \(设 X=\{1,2,3,4,5,6\} 和 Y=\{1,2\}\),由于Y的所有元素都在X中且X包含至少一个不在Y中的元素,那么Y是X的真子集,记做\(Y \subseteq X\).
全集
全集包含特定上下文中的所有元素,在该上下文中所有的集合都是全集的子集. 全集被表示为\(\mathbb{U}\)
例- 定义全集\(U\)是地球上动物,那么哺乳动物就是\(U\)的子集,鱼,昆虫等等都是\({U}\)的子集.
空集
空集不包含任何元素,记做\(\emptyset\). 由于空集的元素个数是有限的,空集是有限集,空集的基是0.
例- \(S=\{x|x\in N \ and \ 7<x<8\}=\emptyset\)
单例集/单位集
单例集只包含一个元素,记做\(\{s\}\)
例- \(S=\{x|x\in N, 7<x<9\} = \{8\}\)
相等集合
两个包含元素全部相同的集合相同.
例- \(如果 A=\{1,2,6\} 和 B=\{6,1,2\}\),那么A和B是相等的,因为A中所有的元素都在B里,且B中所有的元素都在A里.
等价集合
两个基相等的集合叫做等价集合.
例- \(如果 A=\{1,2,6\} 和 B=\{16,17,22\}\),那么A和B是等价的,因为A和B的基相等里,即\(|A|=|B|=3\).
重叠集合
两个至少包含一个相同元素的集合叫重叠集合.
在重叠集合中
- \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\)
- \(n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)\)
- \(n(A) = n(A - B) + n(A \cap B)\)
- \(n(B) = n(B - A) + n(A \cap B)\)
例- 设\(A = \{1,2,6\} 和 B = \{6,12,42\}\). A和B有一个共同元素'6',因此他们是重叠集合.
不相交集
如果集合A和B一个相同的元素都没有则叫做不相交集,不相交集的性质为
- \(n(A \cap B) = \emptyset\)
- \(n(A \cup B) = n(A) + n(B)\)
例- 设\(A = \{1,2,6\} 和 B = \{7,9,14\}\), 它们没有共同的元素,因此为不相交集.
维恩图
维恩图是1880年由John Venn发明的,它可以表示数学集合之间的所有逻辑关系
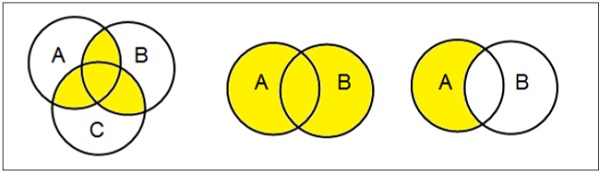
集合的并
集合A,B的并(记做\(A \cup B\))是在A或在B的元素构成的集合. 因此\(A \cup B =\{x|x\in A \;\; OR \; x \in B\}\)
例- \(设A=\{10,11,12,13\} 和 B=\{13,14,15\}\)那么\(A \cup B = \{10,11,12,13,14,15\}\)(相同的元素只出现一次)
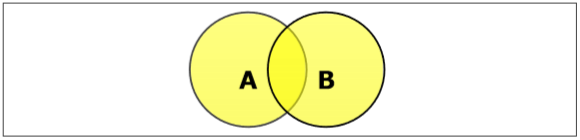
集合的交
集合A,B的交(记做\(A\cap B\))是由即在A也在B的元素构成的集合. 因此\(A \cap B = \{x|x \in A \;\; AND \; x\in B\}\)
例- \(设A=\{11,12,13\}和B=\{13,14,15\}\),那么\(A\cap B = \{13\}\)
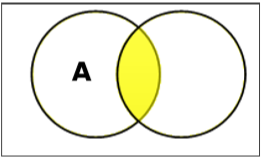
集合的差/相对补集
集合A对B的差(记做\(A-B\))是A集合中不在B集合的元素构成的集合. 因此\(A-B = \{x|x \in A \;\; AND \; x \notin B\}\)
例- \(设A = \{10,11,12,13\} 和 B = \{13,14,15\}, 那么 (A-B) = \{10,11,12\}, (B-A)=\{14,15\}\). 从中我们可以得知\((A-B)\ne (B-A)\)

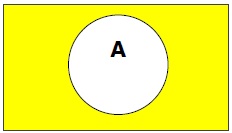
集合的补
集合的补(记做\(A'\))是所有不在A的元素构成的集合. 因此\(A' = \{x|x \notin A\}\),更具体得说\(A' = U-A\),其中\(U\)是包含所有对象的全集
例- \(设A=\{x|x 属于奇数集\}, 那么A' = \{y|y 不属于奇数集\}\)
笛卡尔积/叉积
n个集合的笛卡尔积\(A_1,A_2,\dots A_n\)表示为\(A_1\times A_2 \dots \times A_n\).被定义为所有可能顺序的n元组\((x_1,x_2,\dots x_n)\),其中\(x_1\in A_1,x_2 \in A_2.\dots x_n \in A_n\).
例- 设有两个集合\(A=\{a,b\}和B=\{1,2\}\),
A和B的笛卡尔积被写成\(A \times B = \{(a,1),(a,2),(b,1),(b,2)\}\)
B和A的笛卡尔积被写成\(B \times A = \{(1,a),(1,b),(2,a),(2,b)\}\)
幂集
集合S的幂集是S所有的子集包括空集构成的集合.一个基为n的集合的幂集的基是\(2^n\).幂集记做\(P(S)\)
例- 对于集合\(S = \{a,b,c,d\}\),它的所有子集为:
- 0个元素的子集有 \(\{\emptyset\}\)
- 1个元素的子集有 \(\{a\},\{b\},\{c\},\{d\}\)
- 2个元素的子集有 \(\{a,b\},\{a,c\},,\{a,d\},\{b,c\},\{b,d\},\{c,d\}\)
- 3个元素的子集有 \(\{a,b,c\},\{a,b,d\},,\{a,c,d\},\{b,c,d\}\)
- 4个元素的子集有 \(\{a,b,c,d\}\)
因此 \(P(S)\)=\(\{ \quad \{ \emptyset \}, \{ a \}, \{ b \}, \{ c \}, \{ d \}, \{ a,b \}, \{ a,c \}, \{ a,d \}, \{ b,c \}, \{ b,d \}, \{ c,d \}, \{ a,b,c \}, \{ a,b,d \}, \{ a,c,d \}, \{ b,c,d \}, \{ a,b,c,d \} \quad \}\)
\(|P(S)|=2^4=16\)
注意: 空集的幂集还是空集 \(|P(\{\emptyset\}=2^0=1\)
集合的划分
对一个集合S进行划分,就是切分成n个不相交子集如\(P_1,P_2,\dots P_n\)从而满足三个条件
- \(P_i\)不为空集 $$[P_i \ne {\emptyset} for\quad all 0<i\le n]$$
- 所有子集的并必须为原集合 $$[P_1\cup P_2\cup \dots \cup P_n = S]$$
- 任意两个不同集合的交集为空 $$[P_a \cap P_b = {\emptyset}, for ; a \ne b ; where n \ge a, b \ge 0]$$
例- 设\(S=\{a,b,c,d,e,f,g,h\}\)
一种可能的划分是\(\{a\},\{b,c,d\},\{e,f,g,h\}\)
另一种可能的划分是\(\{a,b\},\{c,d\}.\{e,f,g,h\}\)
贝尔数
一个集合的贝尔数是他所有可能划分的个数.记做\(B_n\)其中n是集合的基.
例- 设\(S=\{1,2,3\}, n =|S| = 3\)
所有可能的划分为
- \(\emptyset,\{1,2,3\}\)
- \(\{1\},\{2,3\}\)
- \(\{1,2\},\{3\}\)
- \(\{1,3\},\{2\}\)
- \(\{1\},\{2\},\{3\}\)
因此\(B_3=5\)
关系
无论讨论什么样的集合,集合间元素的关系都是不可或缺的。关系存在于相一集合的对象中或两个及多个集合的对象中.
定义和性质
集合X对Y的二元关系(写成\(xRy\;或\;R(x,y)\))是笛卡尔积\(x\times y\)的子集.如果关系对中的顺序改变了,那么关系也会相应改变.
通常的,集合\(A_1,\dots , A_n\)的n维关系是它们笛卡尔积\(A_1 \times \dots \times A_n\)的子集. 这种情况下关系R的最小基是0,最大是\(n^2\).
单个集合A的上二元关系就是\(A \times A\)的子集
对于两个不同的集合A(基为m)和B(基为n),A和B的关系中最大的基为\(mn\)
值域和定义域
对于两个集合A和B的关系R有值对(x,y),那么
- R的定义域,Dom(R),是集合 \(\{x|(x,y) \in R 对某些 y \in B\}\)
- R的值域,Ran(R),是集合 \(\{y|(x,y)\in R 对某些 x \in A\}\)
例- 设\(A=\{1,2,9\}, B = \{1,3,7\}\)
- 如果关系是'等于'那么\(R = \{(1,1),(3,3)\}\), $$Dom(R) = \lbrace 1,3 \rbrace, Ran(R) = \lbrace 1,3\rbrace$$
- 如果关系是'小于'那么\(R = \{(1,3),(1,7),(2,3),(2,7)\}\). $$Dom(R) = \lbrace 1,2 \rbrace, Ran(R) = \lbrace 3,7\rbrace$$
- 如果关系是'大于'那么\(R = \{(2,1),(9,1),(9,3),(9,7)\}\). $$Dom(R) = \lbrace 2,9 \rbrace, Ran(R) = \lbrace 1,3,7\rbrace$$
用图来表示关系
关系可以用有向图来表示.
图中顶点的个数等于由关系定义的集合的数量.对于关系中的每个有序对(x,y),用一条从x指向y的有向边来表示,如果有(x,x),那么会出现x到x的子环.
假如在集合\(S = \{1,2,3\}\)上有一个关系 \(R = \{(1,1),(1,2),(3,2)\}\),则用下图表示
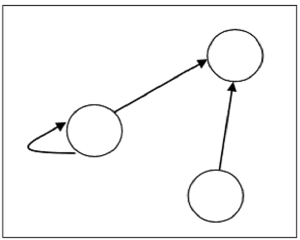
关系的种类
- 集合X到Y的空关系就是空集\(\emptyset\)
- 集合X到Y的全关系就是\(X \times Y\)
- 集合X的单位关系就是\(\{(x,x)| x\in X\}\)
- 关系R的逆关系R'被定义成 - \(R' = \{(b,a)|(a,b)\in R\}\)
例- 如果\(R=\{(1,2),(2,3)\} 那么 R' = \{(2,1),(3,2)\}\)
- 集合A的关系R当满足\(\forall a \in A\)与a有关系(aRa 成立)则被称作自反的
例- 集合\(X = \{a,b\}\) 上的 \(R = \{(a,a),(b,b)\}\) 是自反的
- 集合A的关系R当满足存在\(a \in A\)不与a关系(aRa 不成立)则被称作反自反的
例- 集合\(X = \{a,b\}\) 上的 \(R = \{(a,b),(b,a)\}\) 是反自反的
- 集合A的关系R当满足\(xRy \implies yRx 对 \forall x \in A 和 \forall y \in B\)成立则被称作对称的
例- 集合\(A = \{1,2,3\}\) 上的 \(R = \{(1,2),(2,1),(3,2),(2,3)\}\) 是对称的
- 集合A的关系R当满足存在\(xRy 且 yRx \implies x=y对 \forall x \in A \;且\; \forall y \in B 成立\)则被称作反对称的
例- 关系 \(R = \{(x,y),(b,a) \to N | x \le y\}\) 由于\(x \le y \;且 \; y \le x 蕴含 x=y\) 所以是反对称的
- 集合A上的关系R被称作传递的,当且仅当\(xRy \; 且 \;yRx \;蕴含 \; xRz,\forall x,y,z \in A\)
例- 集合\(A=\{1,2,3\}\)上的关系\(R=\{(1,2),(2,3),(1,3)\}\)是传递的.
- 等价关系必须满足自反性,对称性和传递性
例- 集合\(A=\{1,2,3\}\)上关系\(R=\{(1,1),(2,2),(3,3),(1,2),(2,1),(2,3),(3,2),(1,3),(3,1)\}\)是等价关系.因为他满足自反,对称和传递性.
函数
函数为集合中的每一个元素对应关联集合中的唯一一个元素. 函数有许多的应用,如表示算法的计算复杂度,对象计数,序列的研究和弦论.这一部分的最后一章来描述函数的多方面重要性.
函数的定义
函数或映射(记做\(f: X \to Y\)),表示了从集合X到集合Y元素之间的关系,X被叫做函数的值域,Y是函数的定义域,
函数'f'是在X和Y上的一种关系,满足\(\forall x \in X, 存在一个唯一的 y \in Y 使得 (x,y) \in R\)
方程'f'中'x'被叫做原像,'y'被叫做像.
方程可以一对一或多对一但不能一对多.
单射/一对一函数
函数\(f:A\to B\)满足\(\forall b \in B, 存在至多一个\; a\in A \;满足\; f(a)=b\),则被称为单射或一对一函数.
函数f是单射则有\(a_1 \ne a_2 \implies f(a_1) \ne f(a_2)\)
例-
- \(f:N\to N, f(x) = 5x\) 是单射
- \(f:N\to N, f(x) = x^2\) 是单射
- \(f:R\to R, f(x) = x^2\) 因为\((-x)^2 = x^2\) 所以不是单射
满射/盖射
函数\(f:A\to B\)满足它的像等于它的值域,等价地,对于所有\(b\in B\),存在一些\(a\in A\)使得\(f(a)=b\),即B上的所有元素都可以被A中某个元素经过函数得到,则被称为满射.
例-
- \(f:N \to N, f(x) = x+2\)是满射
- \(f:R \to R, f(x) = x^2\)不是满射,因为实数的平方无法取到负数.
双射/一对一关联
函数\(f:A\to B\)既满足单射也满足满射就是双射.
问
证明函数定义为\(f(x)=2x-3(R\to R)\)是一个双射函数.
解- 我们需要证明这个函数即是单射也是满射
如果\(f(x_1)=f(x_2)\),那么\(2x_1-3=2x_2-3\),可以推出\(x_1=x_2\)
因此,f是单射
由\(2x-3=y\) 推出\(x=(y+5)/3\),属于\(R\)且\(f(x) = y\).
因此,f是满射,
因为f即是单射又是满射,所以f是双射.
函数的逆
一对一关联的函数\(f:A\to B\)的逆是\(g:B\to A\),有如下性质-
\(f(x) = y \Leftrightarrow g(y) = x\)
如果反函数存在,那么这个函数就是可逆的.
例-
- 函数\(f:Z\to Z,f(x) = x+5.\)是可逆的因为它的反函数\(g:Z \to Z, g(x)=x-5\)存在.
- 函数\(f:Z\to Z,f(x)=x^2\)不存在,因为\((-x)^2=x^2\)而不满足一对一
函数的复合
两个函数\(f:A\to B 和 g:B \to C\) 可以被合成成指定形式\(gof\),这是一个定义成\((gof)(x)=g(f(x))\)的A到C的函数
例-
\(设f(x)=x+2,g(x)=2x+1\),找出\((fog)(x)和(gof)(x)\).
解
\((fog)(x)=f(g(x))=f(2x+1)=2x+1+2=2x+3\)
\((gof)(x)=g(f(x))=g(x+2)=2(x+2)+1=2x+5\)
因此\((fog)(x)\ne(gof)(x)\)
复合的一些性质
- 如果f和g是单射,那么(\(gof\))也是一对一
- 如果f和g是满射,那么\((gof)\)也是满射
- 复合满足结合律不满足交换律
原博文地址
https://www.tutorialspoint.com/discrete_mathematics/index.htm


 浙公网安备 33010602011771号
浙公网安备 33010602011771号