算法可视化系列——05归并排序算法——可视化工具链【HTML】

归并排序可视化工具技术深度解析

本篇文章旨在详细解析归并排序可视化工具的设计与实现过程，展示该工具如何通过图形化界面帮助用户直观地理解归并排序算法的核心步骤。在该工具的设计过程中，我们特别考虑了用户体验、性能优化及教学价值的提升。以下是完整的技术解析和架构内容。

🔍 注：本文详细分析一个归并排序可视化HTML页面的设计，展示如何将复杂的分治算法转化为直观的交互式学习工具。

---

🧠 一、归并排序算法原理与复杂度

归并排序采用分治法策略：

1. 分割阶段：将数组递归分割成两半，直到每个子数组只包含一个元素
2. 合并阶段：将两个已排序的子数组合并成一个有序数组

时间复杂度分析：

• 最优：$O(n\log n)$
• 最差：$O(n\log n)$
• 平均：$O(n\log n)$

空间复杂度：$O(n)$（需要额外空间存储临时数组）

稳定性：稳定排序（相同元素保持原始顺序）

---

🎨 二、可视化设计系统

1. 色彩语义编码（Tailwind配置）

colors: {
  primary: '#3B82F6',   // 蓝色 - 未处理元素
  secondary: '#10B981', // 绿色 - 已排序元素
  dividing: '#8B5CF6',  // 紫色 - 分割中
  merging: '#F59E0B',   // 琥珀色 - 合并中
  comparing: '#EF4444'  // 红色 - 比较中
}

2. 响应式布局方案

组件	移动端	桌面端
可视化区域高度	h-64 (16rem)	md:h-80 (20rem)
控制面板布局	单列	三列网格（md:grid-cols-3）
标题字体	text-[clamp(1.8rem,4vw,2.8rem)] 动态适配

3. 动画引擎设计

.bar-transition {
  transition: height 0.3s ease, 
              transform 0.4s ease, 
              background-color 0.2s ease;
}

@keyframes mergePulse {
  0% { transform: scale(1); }
  50% { transform: scale(1.05); }
  100% { transform: scale(1); }
}

.section-marker {
  @apply absolute h-full w-0.5 bg-gray-300 top-0 z-10;
}

---

⚙️ 三、核心算法实现

1. 步骤预生成机制

function generateStepsRecursive(start, end) {
  if (start >= end) return;
  
  const mid = Math.floor((start+end)/2);
  
  // 记录分割步骤
  steps.push({
    type: 'divide',
    start,
    mid,
    end,
    dividers: [mid]
  });
  
  // 递归处理子数组
  generateStepsRecursive(start, mid);
  generateStepsRecursive(mid+1, end);
  
  // 记录合并过程
  steps.push({ type: 'merge_start', start, mid, end });
  
  while (i <= mid && j <= end) {
    steps.push({ type: 'compare', index1: i, index2: j });
    // ...
    steps.push({ type: 'merging', ... });
  }
  
  steps.push({ type: 'merge_complete', start, end });
}

2. 归并排序过程模拟

// 合并操作核心逻辑
while (i <= mid && j <= end) {
  comparisonCount++;
  
  if (array[i] <= array[j]) {
    tempArray[k++] = array[i++];
  } else {
    tempArray[k++] = array[j++];
  }
  
  // 记录部分合并结果
  steps.push({
    type: 'merging',
    mergedPart: [...tempArray.slice(0, k)],
    // ...
  });
}

3. 时间复杂度保障

每次分割将问题规模减半（$O(\log n)$ 层），每层合并操作$O(n)$，整体$O(n\log n)$

---

🖼️ 四、可视化渲染策略

1. 柱状图状态映射

状态	颜色类	触发条件
未处理	bg-primary	默认状态
分割中	bg-dividing	步骤类型为divide
合并中	bg-merging	步骤类型为merge_*
比较中	bg-comparing	步骤类型为compare
已排序	bg-secondary	步骤类型为merge_complete或complete

2. 动态尺寸计算

const height = `${value * 2.5}px`; // 值映射为高度
const barWidth = `calc((100% - ${(n-1)*8}px)/${n})`; // 考虑间距的动态宽度

3. 分割线可视化

// 在分割步骤中渲染分割线
if (highlight.dividers) {
  highlight.dividers.forEach(position => {
    const marker = document.createElement('div');
    marker.className = 'section-marker';
    marker.style.left = `${bar.offsetLeft}px`; // 对齐到柱状图边界
  });
}

---

🕹️ 五、交互控制系统

1. 速度控制算法

const delay = 600 / sortSpeed; // 速度级别1-5

2. 状态管理机

状态	按钮	显示文本
未开始	开始启用	准备就绪
排序中	暂停启用	排序中…
已暂停	继续启用	已暂停
已完成	重置启用	排序完成

3. 关键操作

• 生成新数组：generateRandomArray()
• 重置状态：resetSorting()
• 步骤控制：startSorting(), togglePause()

---

🚀 六、性能优化策略

1. 预计算优化

// 提前生成所有排序步骤
function generateMergeSortSteps() {
  steps = [];
  generateStepsRecursive(0, array.length-1);
  steps.push({ type: 'complete' }); // 最终步骤
}

2. 轻量级数据管理

// 使用浅拷贝避免深拷贝开销
steps.push({
  array: [...array.slice(start, end+1)] 
});

3. 动画帧管理

function continueSorting() {
  // ...
  animationId = setTimeout(continueSorting, delay);
}

function resetSorting() {
  if (animationId) {
    clearTimeout(animationId);
    animationId = null;
  }
}

4. 按需渲染

仅更新当前步骤涉及的元素状态，而非全量重渲染

---

💡 七、教育价值提升

1. 分治策略可视化

清晰展示分割-解决-合并三阶段：

1. 紫色分割线展示数组划分
2. 红色高亮比较操作
3. 橙色展示合并过程

2. 递归过程展示

通过步骤回溯直观展示递归调用栈：

分割 [0-15]
  分割 [0-7]
    分割 [0-3]
    ...
  合并 [0-7]
...

3. 复杂度验证

实时统计指标：

• 比较次数：$C_{mp}\approx n\log n$
• 合并次数：$M_{ge}=n-1$

4. 算法对比实验室

可扩展为多种排序算法比较平台

📊 复杂度对比：当$n=16$时，归并排序比较次数 $\approx$ 64，而冒泡排序 $\approx$ 128，效率提升50%！

---

八、结语

通过此可视化工具，学习者可直观理解归并排序的分治思想：

1. 分割阶段：递归分解问题（$\log n$ 层）
2. 合并阶段：线性合并解（$O(n)$ 每层）
3. 稳定性：保持相同元素原始顺序

项目采用响应式设计，支持从手机到桌面的全设备学习体验，是算法教学领域的优秀范例。

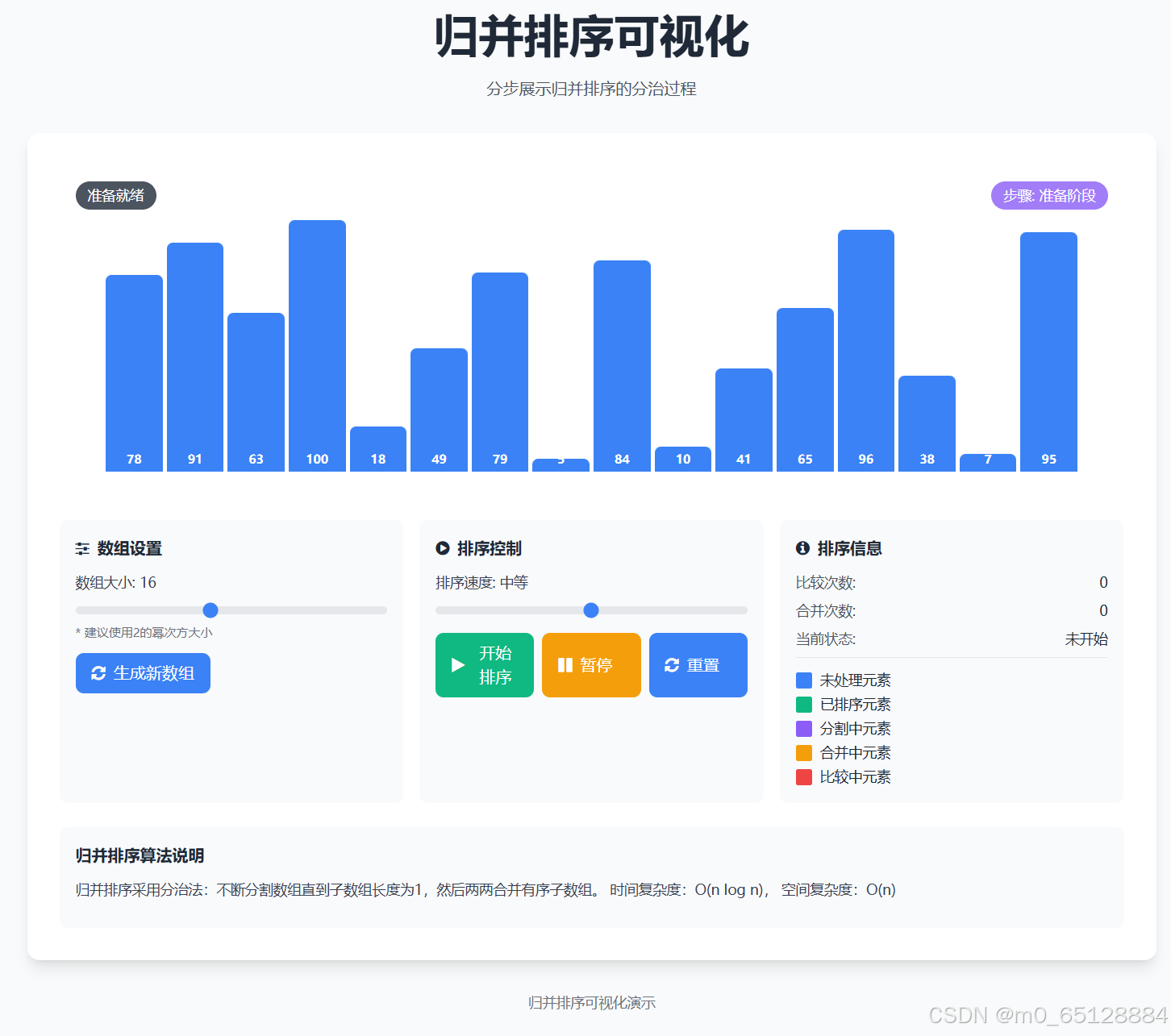
🧩九、结果展示（源码去本人资源区下载）