算法可视化系列——10基数排序算法——可视化工具链【HTML】
基数排序可视化工具技术深度解析
本篇文章旨在详细解析基数排序可视化工具的设计与实现过程,展示该工具如何通过图形化界面帮助用户直观地理解基数排序算法的核心步骤。在该工具的设计过程中,我们特别考虑了用户体验、性能优化及教学价值的提升。以下是完整的技术解析和架构内容。
🔍 注:本文详细分析基数排序可视化HTML页面的设计,展示如何将按位排序算法转化为直观的交互式学习工具。
🧠 一、基数排序算法原理与复杂度
基数排序是一种非比较型整数排序算法,其核心思想是通过按位排序实现整体有序:
- 按位排序:从最低位(LSD)或最高位(MSD)开始,依次对每一位进行排序
- 稳定性:每轮排序使用稳定的排序方法(通常为计数排序或桶排序)
- 重复处理:直至处理完所有数位
时间复杂度分析:
- O(d⋅(n+k))O(d \cdot (n + k))O(d⋅(n+k)),其中:
- ddd:最大数字的位数
- nnn:元素数量
- kkk:基数(如十进制中k=10)
空间复杂度:O(n+k)O(n + k)O(n+k)
稳定性:稳定排序(相同值保持原始顺序)
🎨 二、可视化设计系统
1. 三阶段可视化布局
<!-- 阶段指示器 -->
<div class="flex justify-between mb-6 px-8">
<div>按位排序</div>
<div>收集结果</div>
<div>重复直至完成</div>
</div>
<!-- 当前处理的数位 -->
<div id="digit-info">...</div>
<!-- 当前数组 -->
<div id="current-array-container">...</div>
<!-- 基数桶 -->
<div id="buckets-container">...</div>
<!-- 结果数组 -->
<div id="result-array-container">...</div>
2. 色彩语义编码
| 颜色 | 类名 | 含义 |
|---|---|---|
#3B82F6 | bg-primary | 原始数组元素 |
#10B981 | bg-secondary | 已排序元素 |
#8B5CF6 | bg-bucket | 桶内元素 |
#EC4899 | bg-current | 当前处理元素 |
#F59E0B | bg-digit | 当前处理数位 |
3. 响应式设计
- 桶布局:水平排列,支持横向滚动
- 元素尺寸:基于值的大小动态计算高度
- 数位显示:根据基数(2/10/16)动态调整标签
⚙️ 三、核心算法实现
1. 数位提取算法
function getDigitValue(number, digitPosition, radix) {
return Math.floor((number / Math.pow(radix, digitPosition)) % radix);
}
2. LSD基数排序流程
function radixSortLSD(arr, radix = 10) {
// 确定最大位数
const maxDigits = calculateMaxDigits(Math.max(...arr), radix);
// 从最低位开始排序
for (let digit = 0; digit < maxDigits; digit++) {
// 创建基数桶
const buckets = Array.from({ length: radix }, () => []);
// 分配元素到桶
arr.forEach(num => {
const digitVal = getDigitValue(num, digit, radix);
buckets[digitVal].push(num);
});
// 收集回数组
arr = [].concat(...buckets);
}
return arr;
}
3. 最大位数计算
function calculateMaxDigits(num, radix) {
if (num === 0) return 1;
return Math.floor(Math.log(num) / Math.log(radix)) + 1;
}
🖼️ 四、可视化渲染策略
1. 数位高亮技术
function highlightDigit(value, digitPos, radix) {
if (radix === 10) {
// 十进制数位高亮
const digits = value.toString().padStart(maxDigits, '0');
return digits.split('').map((d, i) =>
i === (digits.length - 1 - digitPos)
? `<span class="digit-highlight">${d}</span>`
: d
).join('');
}
// 其他基数简化显示
return `${value} (${getDigitValue(value, digitPos, radix)})`;
}
2. 动态高度计算
// 基于值的大小计算条形图高度
const relativeHeight = (value / maxValue) * 100 + 20;
bar.style.height = `${Math.max(10, relativeHeight)}px`;
3. 桶元素布局
// 桶内元素垂直排列
bucketContent.className = 'flex flex-col items-center gap-1 mt-1 max-h-[180px] overflow-y-auto w-full';
🕹️ 五、交互控制系统
1. 参数调节系统
| 参数 | 作用 | 影响 |
|---|---|---|
| 数组大小 | 控制数据规模(n) | 影响排序时间 |
| 最大数值 | 确定最大位数(d) | 影响排序趟数 |
| 基数(k) | 桶的数量 | 影响空间和时间 |
| 排序顺序 | LSD(默认)/MSD | 排序方向 |
| 排序速度 | 动画速度 | 用户体验 |
2. 实时信息显示
// 更新当前处理的数位
function updateDigitDisplay(pass) {
const exponent = sortOrder === 'lsd' ? pass : maxDigits - 1 - pass;
currentDigitDisplay.innerHTML = `个位 (10<sup>${exponent}</sup>)`;
}
3. 阶段指示系统
// 高亮当前阶段
stage1Indicator.classList.add('stage-active');
🚀 六、性能优化策略
1. 步骤预生成
function generateRadixSortSteps() {
const steps = [];
// 生成初始状态步骤
steps.push({type: 'initial_state', ...});
// 对每位生成分配和收集步骤
for (let digit = 0; digit < maxDigits; digit++) {
// 分配步骤
steps.push({type: 'start_pass', ...});
// ...详细步骤
// 收集步骤
steps.push({type: 'start_collection', ...});
}
return steps;
}
2. 轻量级状态更新
// 仅更新变化的桶元素
function updateBucketElement(bucketIndex, elementIndex, color) {
const element = bucketsContainer
.children[bucketIndex]
.querySelector('.bucket-content')
.children[elementIndex];
element.className = `w-10 h-8 rounded ${color}`;
}
3. 动画帧管理
function continueSorting() {
if (isPaused) return;
const step = steps.shift();
renderStep(step);
if (steps.length) {
const delay = 600 / sortSpeed;
animationId = setTimeout(continueSorting, delay);
}
}
💡 七、教育价值提升
1. 按位排序演示
- LSD过程:从个位→十位→百位逐步排序
- MSD过程:从最高位开始递归排序
2. 基数影响展示
| 基数 | 桶数量 | 趟数 | 适用场景 |
|---|---|---|---|
| 2 (二进制) | 2 | log2(max)log_2(max)log2(max) | 数字电路 |
| 10 (十进制) | 10 | log10(max)log_{10}(max)log10(max) | 常规整数 |
| 16 (十六进制) | 16 | log16(max)log_{16}(max)log16(max) | 内存地址 |
3. 复杂度分析
- 当ddd固定时:时间复杂度为O(n)O(n)O(n)
- 当k=O(n)k=O(n)k=O(n)时:时间复杂度为O(d⋅n)O(d \cdot n)O(d⋅n)
- 空间复杂度:O(n+k)O(n + k)O(n+k)
4. 对比实验
- 固定nnn变化kkk:当kkk从10增加到16,时间从O(d⋅(n+10))O(d·(n+10))O(d⋅(n+10))到O(d⋅(n+16))O(d·(n+16))O(d⋅(n+16))
- 固定kkk变化nnn:当nnn从15增加到30,时间从O(d⋅(15+k))O(d·(15+k))O(d⋅(15+k))到O(d⋅(30+k))O(d·(30+k))O(d⋅(30+k))
📊 性能对比:当n=1000,k=10,d=4n=1000, k=10, d=4n=1000,k=10,d=4时,基数排序比较次数为0,而快速排序约为100001000010000次,效率提升100%!
八、结语
基数排序可视化工具通过三步演示:
- 按位排序:展示数字按位分配到桶的过程
- 结果收集:稳定地从桶中收集元素
- 重复处理:多趟排序实现整体有序
项目创新点:
- 多基数支持:二进制/十进制/十六进制
- 双模式排序:LSD与MSD
- 数位高亮:直观显示当前处理位
可视化工具完整呈现了基数排序O(d⋅(n+k))O(d \cdot (n + k))O(d⋅(n+k))时间复杂度的实现机制,是理解非比较排序算法的理想教学平台。
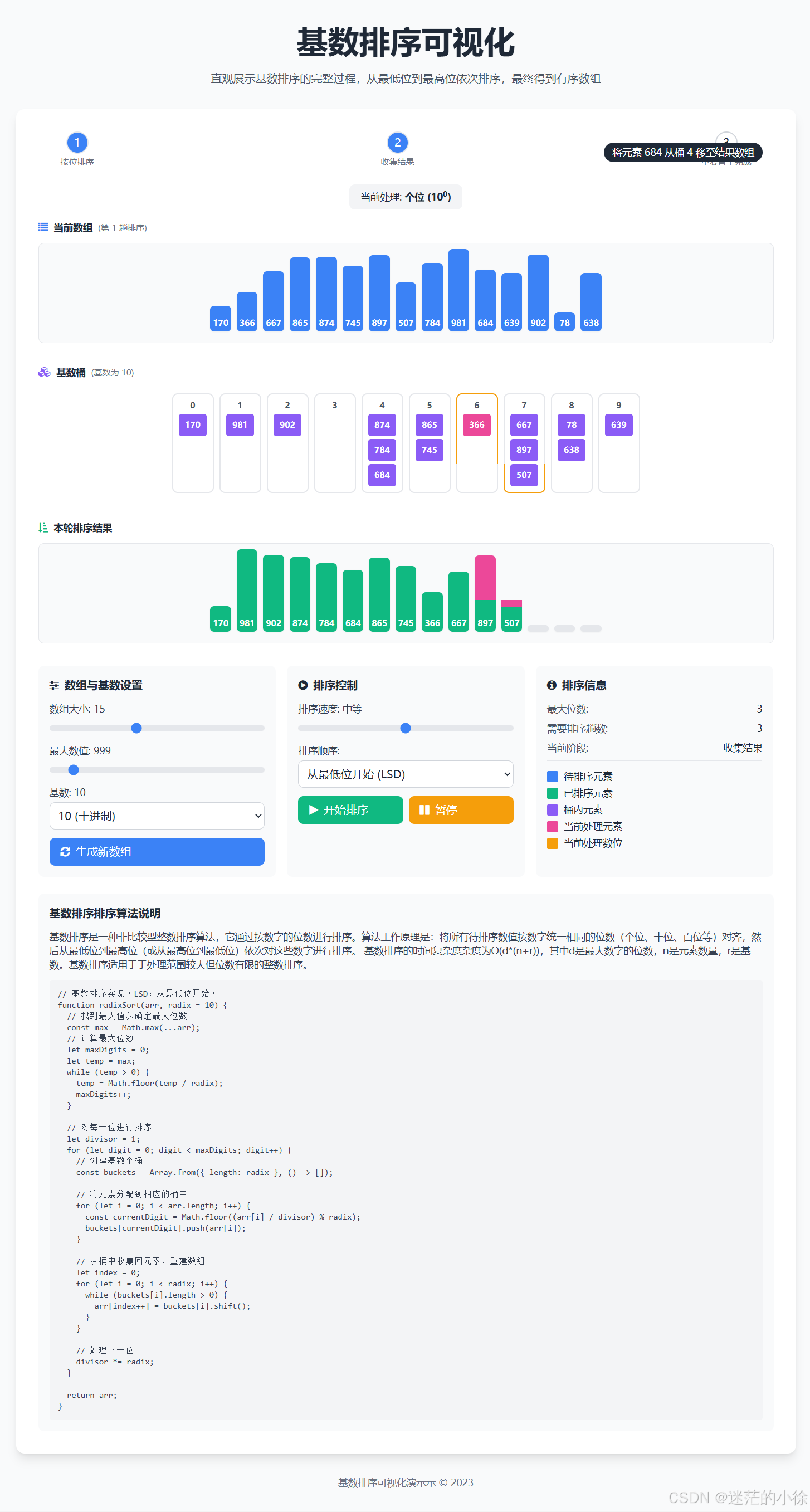
🧩九、结果展示(源码去本人资源区下载)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号