【HTML 勾股定理可视互动，秒懂平方和】——筑梦教育网页新视界

🔺 勾股定理教学互动演示技术解析

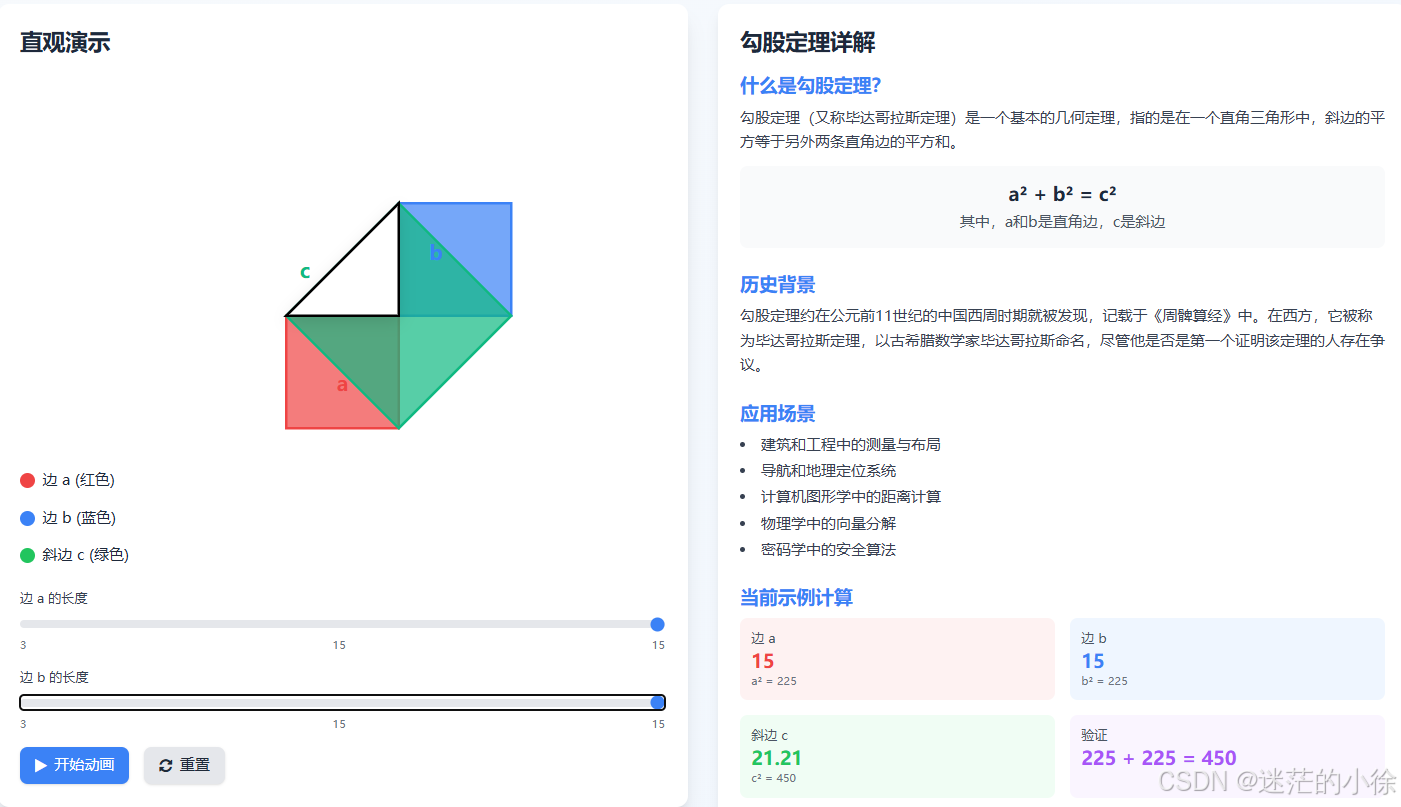
一、📐 设计理念与架构

这个勾股定理教学工具通过动态可视化与交互式学习将抽象数学概念转化为直观体验：

1.1 教学可视化架构

├── 动态演示区
│   ├── 可调节直角三角形
│   ├── 三边正方形可视化
│   └── 实时计算面板
├── 知识讲解区
│   ├── 定理定义
│   ├── 历史背景
│   ├── 应用场景
│   └── 验证计算
└── 学习扩展区
    └── 常见勾股数示例

1.2 技术栈

<!-- 核心库 -->
<script src="https://cdn.tailwindcss.com"></script>
<link href="https://cdn.jsdelivr.net/npm/font-awesome@4.7.0/css/font-awesome.min.css" rel="stylesheet">

<!-- 动态绘图 -->
<svg> <!-- 使用原生SVG绘制几何图形 -->

二、🎨 视觉设计系统

2.1 色彩编码系统

colors: {
    primary: '#3B82F6',   // 主色(数学蓝)
    secondary: '#10B981', // 成功色(验证绿)
    accent: '#F59E0B',   // 强调色(注意黄)
    dark: '#1E293B',     // 深色文本
    light: '#F8FAFC'     // 浅色背景
}

• 边a: 红色(#EF4444)
• 边b: 蓝色(#3B82F6)
• 斜边c: 绿色(#10B981)

2.2 响应式布局

<div class="grid grid-cols-1 lg:grid-cols-2 gap-8">
    <!-- 左侧: 交互演示区 -->
    <!-- 右侧: 知识讲解区 -->
</div>

三、📐 核心交互功能

3.1 动态三角形绘制

function drawTriangleAndSquares(a, b) {
    // 计算斜边
    const c = Math.sqrt(a * a + b * b);
    
    // 创建SVG元素
    const svg = document.createElementNS('http://www.w3.org/2000/svg', 'svg');
    
    // 三角形顶点坐标
    const x1 = /* 计算 */, y1 = /* 计算 */;
    const x2 = /* 计算 */, y2 = /* 计算 */;
    const x3 = /* 计算 */, y3 = /* 计算 */;
    
    // 绘制三角形
    const triangle = document.createElementNS('http://www.w3.org/2000/svg', 'polygon');
    triangle.setAttribute('points', `${x1},${y1} ${x2},${y2} ${x3},${y3}`);
    
    // 绘制三个正方形
    drawSquare(x1, y1, a, 'red');     // 边a正方形
    drawSquare(x2, y2, b, 'blue');    // 边b正方形
    drawSquare(x1, y1, c, 'green');   // 斜边c正方形
}

3.2 实时计算系统

function updateCalculations() {
    const aSq = a * a;
    const bSq = b * b;
    const cSq = aSq + bSq;
    
    // 更新显示
    document.getElementById('calc-a').textContent = a;
    document.getElementById('a-squared').textContent = aSq;
    document.getElementById('verification').textContent = `${aSq} + ${bSq} = ${cSq}`;
}

四、✨ 动态效果系统

4.1 视觉反馈动画

@keyframes pulse {
    0% { transform: scale(1); opacity: 0.7; }
    50% { transform: scale(1.05); opacity: 0.9; }
    100% { transform: scale(1); opacity: 0.7; }
}

4.2 三边同步动画

function animateSquares() {
    const squareA = document.getElementById('square-a');
    const squareB = document.getElementById('square-b');
    const squareC = document.getElementById('square-c');
    
    // 依次触发动画
    squareA.style.animation = 'pulse 1s ease-in-out 0s 2';
    squareB.style.animation = 'pulse 1s ease-in-out 0.5s 2';
    squareC.style.animation = 'pulse 1s ease-in-out 1s 2';
}

五、📚 教学内容设计

5.1 定理定义区

<div class="bg-gray-50 p-4 rounded-lg">
    <p class="text-center text-xl font-bold text-dark">a² + b² = c²</p>
    <p class="text-center text-gray-600 mt-1">其中，a和b是直角边，c是斜边</p>
</div>

5.2 历史背景区

“勾股定理约在公元前11世纪的中国西周时期就被发现，记载于《周髀算经》中…”

5.3 应用场景

<ul class="list-disc list-inside text-gray-700 space-y-1">
    <li>建筑和工程中的测量与布局</li>
    <li>导航和地理定位系统</li>
    <li>计算机图形学中的距离计算</li>
</ul>

5.4 验证计算区

<div class="bg-red-50 p-3 rounded-lg">
    <p class="text-sm text-gray-600">边 a</p>
    <p class="text-xl font-bold text-red-500">3</p>
    <p class="text-xs text-gray-500">a² = 9</p>
</div>

六、🧮 学习扩展区

6.1 勾股数示例

<div class="grid grid-cols-1 sm:grid-cols-2 md:grid-cols-3 gap-4">
    <div class="bg-gray-50 p-4 rounded-lg square-hover">
        <h3 class="font-semibold text-primary mb-2">3-4-5</h3>
        <p class="text-gray-700">3² + 4² = 5²</p>
        <p class="text-gray-600 text-sm mt-1">9 + 16 = 25</p>
    </div>
    <!-- 更多示例... -->
</div>

七、💡 教学创新点

1. 动态验证：通过滑块实时展示 $a^2+b^2=c^2$ 的关系
2. 视觉编码：不同颜色区分三边及其正方形面积
3. 历史背景：结合中西方的数学史增强文化维度
4. 应用场景：展示定理在现代科技中的应用价值
5. 交互记忆：动画强化对面积关系的理解

八、🚀 技术亮点

1. 纯SVG渲染：无依赖绘制几何图形
2. 响应式比例：自动缩放适应容器大小
3. 实时计算：即时更新所有相关数据
4. CSS动画：轻量级交互动效
5. 模块化设计：清晰分离演示与教学内容

九、🎓 教学价值

这个演示工具通过：

1. 视觉化：将抽象公式转化为直观图形
2. 交互性：学生可自主探索不同边长组合
3. 多维度：结合历史、应用和数学验证
4. 即时反馈：调整参数立即看到效果变化

完美展示了如何利用Web技术将经典数学定理转化为沉浸式学习体验，使勾股定理不再是一个需要死记硬背的公式，而是一个可以直观理解和探索的几何关系。

十、结果展示