骏码杯I题：最大公约数求和

 

 

原理：

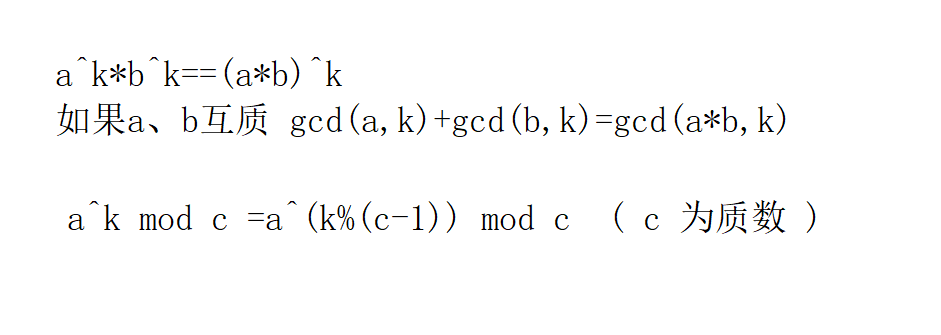
题解在代码里，如下

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> PLL;
#define IOS cin.tie(nullptr)->sync_with_stdio(false);
#define se second
#define fi first
#define mem(a,b) memset(a,b,sizeof a);
#define pri priority_queue<int,vector<int>,greater<int> >
#define low(a,b,c) lower_bound(a,a+b,c)-a;
#define upp(a,b,c) upper_bound(a,a+b,c)-a;
const int N=2e7+7;
const LL mod=1e9+7;
bool st[N];
int p[N],tot;
LL x[N],y[N];
LL n,k;

/*
   积性函数 ；f(ab)=f(a)f(b) （可以参考质数筛） 
*/
LL pow_mod(LL a,LL b){
	LL ret=1;
	LL p=mod;
	while(b){
		if((b&1)) ret=(ret*a)%p; 
		a=(a*a)%p;
		b>>=1;
	}
	return ret;
}
void solve()
{
	cin>>n>>k;
	x[1]=y[1]=1;
	LL ans=1;
	for(int i=2;i<=n;i++)
	{
		if(!st[i]) //这里判断是否被标记过 
		{
			p[tot++]=i; //进入队列 
			y[i]=pow_mod(i,k%(mod-1); //欧拉降幂 
			x[i]=__gcd(1LL*i,k); 
		}
		for(int j=0;i*p[j]<=n&&j<tot;j++)//枚举 
		{
			st[p[j]*i]=true; //标记 
			y[i*p[j]]=(y[i]*y[p[j]])%mod; //满足积性函数 
			
			if(i%p[j]==0) //减枝	 p[j] 为 i的质因数  记为w 
			{
				if((k/x[i])%p[j]==0) x[i*p[j]]=(x[i]*p[j])%mod;//这里的意思是 K%2w==0 ,既2w为k的因数; 
				else x[i*p[j]]=x[i]; //否则 k只包含一个w 只需要等价于 x[i] 就行  
				break;
			}
			x[i*p[j]]=x[p[j]]*x[i]; //这里 i和p[j] 一定没有大于1的公因数 ，直接利用积性函数性质即刻 
			
		}
		ans=(ans+x[i]*y[i])%mod;
	}
	cout<<ans<<"\n";
}
int main()
{
	int t=1;
	while(t--)
	{
		solve();
	}
	return 0;
}