数的拆分

 

 

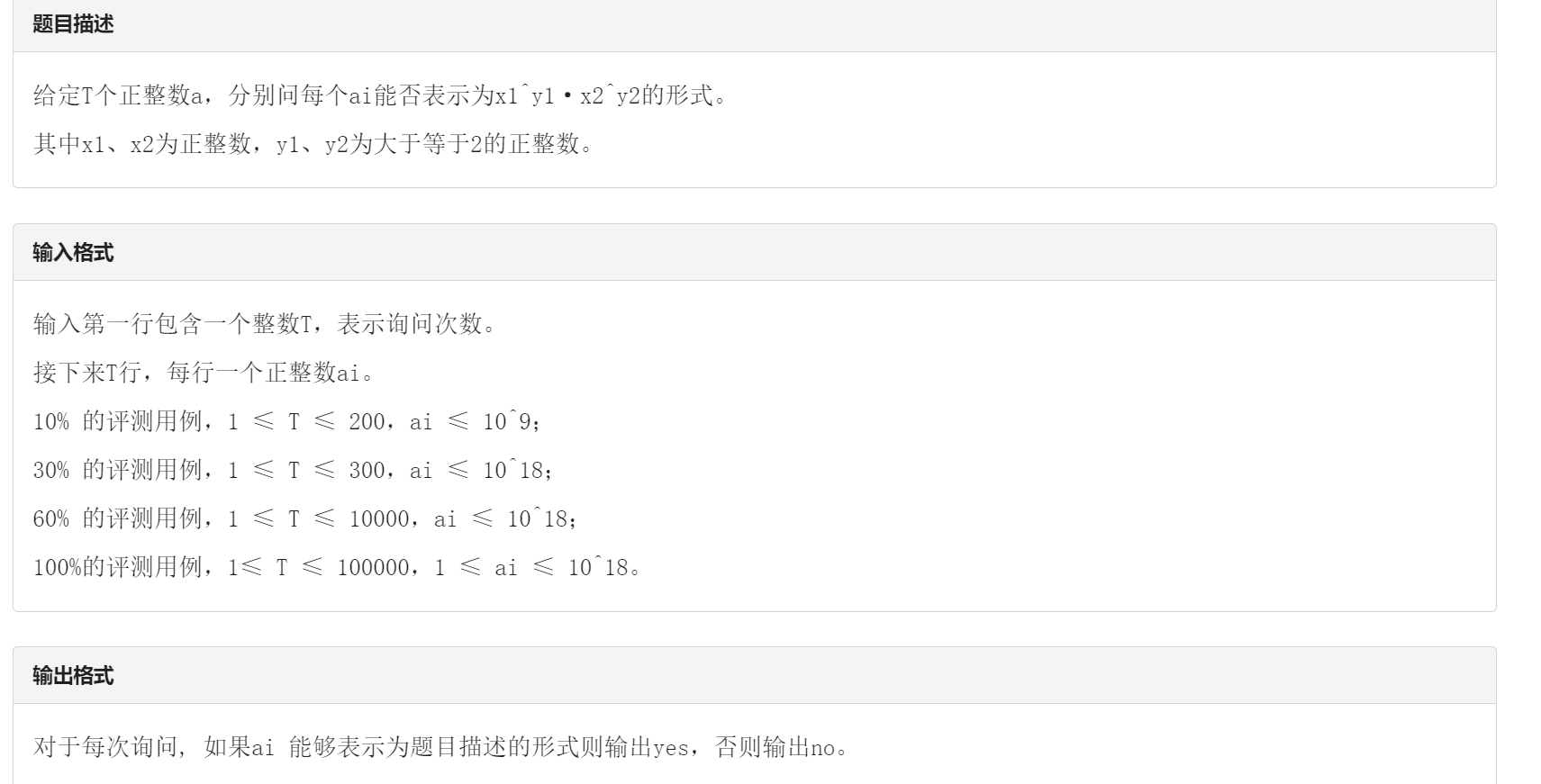
思路：一定能拆成 x1的二次方，x2的三次方。当把数分解成质因数乘积后，如果有单独的质数，一定不合理， 也就是说如果有质因数，每种质因数最低有两个 ，从而如果同意质因数大于2且为偶数 ，就可以合成两个荷和数，放x1中，如果为奇数，先拿出三个，放入x2中，剩下的放入x1中。 这里需要用质数筛预处理4000以内的质数。因为剩余n只能为之后质数的3次方或二次方，并且如果成立（yes），必然只存在一种质因数，且不超三次方，只需要check一下就好了。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=4000+7;
bool p[N];
int prime[N],idx=0;
void init()
{
	for(int i=2;i<N;i++)
	{
		if(!p[i]) prime[++idx]=i;
		for(int j=1;j<=idx&&prime[j]*i<N;j++)
		{
			p[prime[j]*i]=true;
			if(i%prime[j]==0) break;
		}
	}
}
bool check(ll x)
{
	ll l=1,r=1e9;
	while(l<r)
	{
		ll mid=(l+r)>>1;
		if(mid*mid<x)
		{
			l=mid+1;
		}
		else
		{
			r=mid;
		}
	}
	if(l*l==x) return true;
	 l=1,r=1e6;
	while(l<r)
	{
		ll mid=(l+r)>>1;
		if(mid*mid*mid<x)
		{
			l=mid+1;
		}
		else
		{
			r=mid;
		}
	}
	if(l*l*l==x) return true;
	return false;
}
int main()
{
	ios:;sync_with_stdio(0);
	cin.tie(0);
	init();
//	cout<<idx<<endl;
//	for(int i = 1; i<=idx;i++)
//	cout<<prime[i]<<" ";
	int t;
	long long n;
	cin>>t;
	int flag;
	while(t--)
	{
		cin>>n;
		flag=0;
		for(int i=1;i<=idx;i++)
		{
			int t=0;
			while(!(n%prime[i]))
			{
				n=n/prime[i];
				t++;
			}
			if(t==1) 
			{
				flag=1;
				break;
			}
		}
		if(!flag&&check(n))
		{
			cout<<"yes\n";
		}
		else cout<<"no\n";
		
	}
	return 0;
}