椭圆型方程网格生成法 - Python实现

  • 算法特征
    ①. 给定边界条件; ②. 在物理空间构建椭圆型方程; ③. 在计算空间求解椭圆型方程
  • 算法推导
    以2维物理空间$(x, y)$及计算空间$(\xi,\eta)$为例, 不失一般性, 令存在如下变换关系,
    \begin{equation}
    \left\{
    \begin{split}
    \xi = \xi(x, y) \\
    \eta = \eta(x, y)
    \end{split}
    \right.
    \label{eq_1}
    \end{equation}
    其中, $(x, y)$为单连通任意形状区域, $(\xi, \eta)$为单连通矩形区域. 经过上式$\eqref{eq_1}$变换, 物理空间边界对应计算空间边界, 物理空间内点对应计算空间内点.
    直接通过给定边界条件求解PDE以获取内点映射关系, 通常应当建立椭圆型方程. 进一步, 在物理空间中构建如下Poisson's equations具体描述式$\eqref{eq_1}$之变换关系,
    \begin{equation}
    \begin{split}
    \frac{\partial^2\xi}{\partial x^2} + \frac{\partial^2\xi}{\partial y^2} &= P(x,y) \\
    \frac{\partial^2\eta}{\partial x^2} + \frac{\partial^2\eta}{\partial y^2} &= Q(x,y)
    \end{split}
    \label{eq_2}
    \end{equation}
    现考虑将物理空间之PDE转换至计算空间, 由于,
    \begin{equation}
    \left\{
    \begin{split}
    \frac{\partial x}{\partial x} &= x_\xi\xi_x + x_\eta\eta_x = 1 \\
    \frac{\partial x}{\partial y} &= x_\xi\xi_y + x_\eta\eta_y = 0 \\
    \frac{\partial y}{\partial x} &= y_\xi\xi_x + y_\eta\eta_x = 0 \\
    \frac{\partial y}{\partial y} &= y_\xi\xi_y + y_\eta\eta_y = 1 \\
    \end{split}
    \right.
    \label{eq_3}
    \end{equation}
    求解上式$\eqref{eq_3}$得,
    \begin{equation}
    \xi_x = \frac{y_\eta}{J}\quad \xi_y=\frac{-x_\eta}{J}\quad \eta_x=\frac{-y_\xi}{J}\quad \eta_y=\frac{x_\xi}{J}
    \label{eq_4}
    \end{equation}
    其中, $\displaystyle J = |\partial(x, y)/\partial(\xi,\eta)| = x_\xi y_\eta - y_\xi x_\eta$.
    由于,
    \begin{equation}
    \left\{
    \begin{split}
    \frac{\partial^2x}{\partial x^2}&=x_{\xi\xi}\xi_x^2 + x_{\eta\eta}\eta_x^2 + 2x_{\xi\eta}\xi_x\eta_x + x_\xi\xi_{xx} + x_\eta\eta_{xx} = 0 \\
    \frac{\partial^2x}{\partial y^2}&=x_{\xi\xi}\xi_y^2 + x_{\eta\eta}\eta_y^2 + 2x_{\xi\eta}\xi_y\eta_y + x_\xi\xi_{yy} + x_\eta\eta_{yy} = 0 \\
    \frac{\partial^2y}{\partial x^2}&=y_{\xi\xi}\xi_x^2 + y_{\eta\eta}\eta_x^2 + 2y_{\xi\eta}\xi_x\eta_x + y_\xi\xi_{xx} + y_\eta\eta_{xx} = 0 \\
    \frac{\partial^2y}{\partial y^2}&=y_{\xi\xi}\xi_y^2 + y_{\eta\eta}\eta_y^2 + 2y_{\xi\eta}\xi_y\eta_y + y_\xi\xi_{yy} + y_\eta\eta_{yy} = 0 \\
    \end{split}
    \right.
    \label{eq_5}
    \end{equation}
    结合式$\eqref{eq_2}$、式$\eqref{eq_4}$, 上式$\eqref{eq_5}$转换如下,
    \begin{equation}
    \begin{split}
    \alpha x_{\xi\xi} - 2\beta x_{\xi\eta} + \gamma x_{\eta\eta} + J^2(Px_\xi+Qx_\eta) = 0 \\
    \alpha y_{\xi\xi} - 2\beta y_{\xi\eta} + \gamma y_{\eta\eta} + J^2(Py_\xi+Qy_\eta) = 0 \\
    \end{split}
    \label{eq_6}
    \end{equation}
    其中, $\alpha = x_\eta^2 + y_\eta^2$, $\beta=x_\xi x_\eta+y_\xi y_\eta$, $\gamma=x_\xi^2 + y_\xi^2$. 上式$\eqref{eq_6}$即计算空间中待求解之椭圆型方程.
    由于大型方程组求解的本质困难, 本文拟采用含时演化技术将椭圆型方程转换为抛物型方程进行求解. 如果含时演化的抛物型方程最终趋于稳定, 则收敛于相应椭圆型方程的解. 式$\eqref{eq_6}$椭圆型方程转换后的抛物型方程如下,
    \begin{equation}
    \begin{split}
    x_t &= \alpha x_{\xi\xi} - 2\beta x_{\xi\eta} + \gamma x_{\eta\eta} + J^2(Px_\xi+Qx_\eta) = 0 \\
    y_t &= \alpha y_{\xi\xi} - 2\beta y_{\xi\eta} + \gamma y_{\eta\eta} + J^2(Py_\xi+Qy_\eta) = 0 \\
    \end{split}
    \label{eq_7}
    \end{equation}
    实际操作中, 通常将计算空间$(\xi,\eta)$取为物理空间$(x,y)$离散化后的下标值, 因此各方向相邻网格节点之间距$\Delta\xi = \Delta\eta = 1$. 本文拟采用如下差分格式离散化式$\eqref{eq_7}$各微分项(以$x$为例),
    \begin{equation}
    \left\{
    \begin{split}
    x_\xi &= \frac{x_{i+1,j} - x_{i-1,j}}{2} \\
    x_\eta &= \frac{x_{i,j+1} - x_{i, j-1}}{2} \\
    x_{\xi\xi} &= x_{i+1,j} + x_{i-1,j} - 2x_{i,j} \\
    x_{\eta\eta} &= x_{i,j+1} + x_{i,j-1} - 2x_{i,j} \\
    x_{\xi\eta} &= \frac{x_{i+1,j+1} + x_{i-1,j-1} - x_{i+1,j-1} - x_{i-1,j+1}}{4} \\
    x_t &= \frac{x^{k+1}-x^k}{h_t} \\
    \end{split}
    \right.
    \label{eq_8}
    \end{equation}
    注意, 式$\eqref{eq_7}$之求解需要配合初始条件及边界条件, 本文重在获取其稳态解, 因此对初始条件不作具体要求, 边界条件则根据物理空间边界与计算空间边界之映射关系灵活给出. 若,
    \begin{equation}
    \|X^{k+1} - X^k\| < \epsilon\quad \&\quad \|Y^{k+1} - Y^k\|<\epsilon
    \label{eq_9}
    \end{equation}
    其中, $\epsilon$取值足够小正数, 则$X^k$、$Y^k$均趋于稳定并收敛于式$\eqref{eq_6}$的解, 此即物理空间中根据椭圆型方程生成的网格节点.
  • 代码实现
    现以如下翼型为例进行算法实施,
    \begin{equation*}
    y=0.1781\sqrt{x}-0.0756x-0.2122x^2+0.1705x^3-0.0609x^4, \quad \text{where }x\in[0,1]
    \end{equation*}
    令$P=Q=0$, 通过求解无源Laplace's eqautions进行网格生成, 具体实现如下,
      1 # 椭圆型方程网格生成法
  2 
  3 import numpy
  4 from matplotlib import pyplot as plt
  5 
  6 
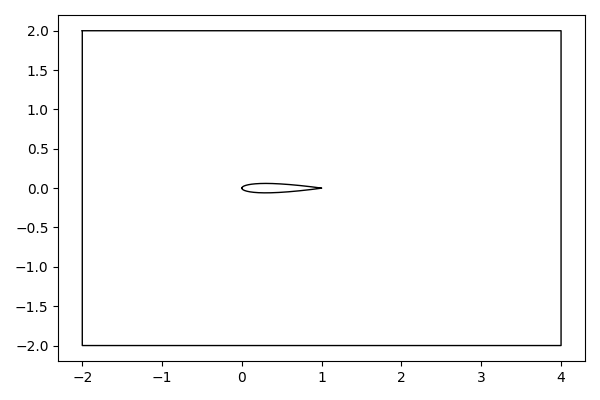
  7 # 对称翼型的上半部
  8 def half_wing(x):
  9     funcVal = 0.1781 * numpy.sqrt(x) - 0.0756 * x - 0.2122 * x ** 2 + 0.1705 * x ** 3 - 0.0609 * x ** 4
 10     return funcVal
 11     
 12 
 13 # 构造物理空间与计算空间边界映射关系
 14 def build_bdy_maps():
 15     p2c_xi = [
 16         ((1.0, 0.0), (0, 15)),
 17         ((0.9, half_wing(0.9)), (1, 15)),
 18         ((0.8, half_wing(0.8)), (2, 15)),
 19         ((0.7, half_wing(0.7)), (3, 15)),
 20         ((0.6, half_wing(0.6)), (4, 15)),
 21         ((0.5, half_wing(0.5)), (5, 15)),
 22         ((0.4, half_wing(0.4)), (6, 15)),
 23         ((0.3, half_wing(0.3)), (7, 15)),
 24         ((0.2, half_wing(0.2)), (8, 15)),
 25         ((0.1, half_wing(0.1)), (9, 15)),
 26         ((0.0, half_wing(0.0)), (10, 15)),
 27         ((0.1, -half_wing(0.1)), (11, 15)),
 28         ((0.2, -half_wing(0.2)), (12, 15)),
 29         ((0.3, -half_wing(0.3)), (13, 15)),
 30         ((0.4, -half_wing(0.4)), (14, 15)),
 31         ((0.5, -half_wing(0.5)), (15, 15)),
 32         ((0.6, -half_wing(0.6)), (16, 15)),
 33         ((0.7, -half_wing(0.7)), (17, 15)),
 34         ((0.8, -half_wing(0.8)), (18, 15)),
 35         ((0.9, -half_wing(0.9)), (19, 15)),
 36         ((1.0, 0.0), (20, 15)),
 37         ((4.0, 0.0), (0, 0)),
 38         ((4.0, 1.0), (1, 0)),
 39         ((4.0, 2.0), (2, 0)),
 40         ((3.0, 2.0), (3, 0)),
 41         ((2.0, 2.0), (4, 0)),
 42         ((1.0, 2.0), (5, 0)),
 43         ((0.0, 2.0), (6, 0)),
 44         ((-1.0, 2.0), (7, 0)),
 45         ((-2.0, 2.0), (8, 0)),
 46         ((-2.0, 1.0), (9, 0)),
 47         ((-2.0, 0.0), (10, 0)),
 48         ((-2.0, -1.0), (11, 0)),
 49         ((-2.0, -2.0), (12, 0)),
 50         ((-1.0, -2.0), (13, 0)),
 51         ((0.0, -2.0), (14, 0)),
 52         ((1.0, -2.0), (15, 0)),
 53         ((2.0, -2.0), (16, 0)),
 54         ((3.0, -2.0), (17, 0)),
 55         ((4.0, -2.0), (18, 0)),
 56         ((4.0, -1.0), (19, 0)),
 57         ((4.0, 0.0), (20, 0))
 58     ]
 59     
 60     p2c_eta = [
 61         ((4.0, 0.0), (0, 0)),
 62         ((3.8, 0.0), (0, 1)),
 63         ((3.6, 0.0), (0, 2)),
 64         ((3.4, 0.0), (0, 3)),
 65         ((3.2, 0.0), (0, 4)),
 66         ((3.0, 0.0), (0, 5)),
 67         ((2.8, 0.0), (0, 6)),
 68         ((2.6, 0.0), (0, 7)),
 69         ((2.4, 0.0), (0, 8)),
 70         ((2.2, 0.0), (0, 9)),
 71         ((2.0, 0.0), (0, 10)),
 72         ((1.8, 0.0), (0, 11)),
 73         ((1.6, 0.0), (0, 12)),
 74         ((1.4, 0.0), (0, 13)),
 75         ((1.2, 0.0), (0, 14)),
 76         ((1.0, 0.0), (0, 15)),
 77         ((4.0, 0.0), (20, 0)),
 78         ((3.8, 0.0), (20, 1)),
 79         ((3.6, 0.0), (20, 2)),
 80         ((3.4, 0.0), (20, 3)),
 81         ((3.2, 0.0), (20, 4)),
 82         ((3.0, 0.0), (20, 5)),
 83         ((2.8, 0.0), (20, 6)),
 84         ((2.6, 0.0), (20, 7)),
 85         ((2.4, 0.0), (20, 8)),
 86         ((2.2, 0.0), (20, 9)),
 87         ((2.0, 0.0), (20, 10)),
 88         ((1.8, 0.0), (20, 11)),
 89         ((1.6, 0.0), (20, 12)),
 90         ((1.4, 0.0), (20, 13)),
 91         ((1.2, 0.0), (20, 14)),
 92         ((1.0, 0.0), (20, 15))
 93     ]
 94     
 95     return p2c_xi, p2c_eta
 96     
 97     
 98 class EllipticGrid(object):
 99     
100     def __init__(self, p2c_xi, p2c_eta):
101         self.__p2c_xi = p2c_xi                           # 物理空间与计算空间xi轴边界映射关系
102         self.__p2c_eta = p2c_eta                         # 物理空间与计算空间eta轴边界映射关系
103     
104         self.__n_xi, self.__n_eta = self.__get_n()       # 计算空间子区间划分数
105         self.__ht = 0.1
106         
107         self.__bdyX, self.__bdyY = self.__get_bdy()
108     
109     
110     def get_solu(self, maxIter=1000000, epsilon=1.e-9):
111         '''
112         数值求解
113         maxIter: 最大迭代次数
114         epsilon: 收敛判据
115         '''
116         X0 = self.__get_initX()
117         Y0 = self.__get_initY()
118         
119         for i in range(maxIter):
120             Xx = self.__calc_Ux(X0)
121             Xe = self.__calc_Ue(X0)
122             Xxx = self.__calc_Uxx(X0)
123             Xee = self.__calc_Uee(X0)
124             Xxe = self.__calc_Uxe(X0)
125             Yx = self.__calc_Ux(Y0)
126             Ye = self.__calc_Ue(Y0)
127             Yxx = self.__calc_Uxx(Y0)
128             Yee = self.__calc_Uee(Y0)
129             Yxe = self.__calc_Uxe(Y0)
130             
131             alpha = self.__calc_alpha(Xe, Ye)
132             beta = self.__calc_beta(Xx, Xe, Yx, Ye)
133             gamma = self.__calc_gamma(Xx, Yx)
134             
135             Kx = alpha * Xxx - 2 * beta * Xxe + gamma * Xee
136             Ky = alpha * Yxx - 2 * beta * Yxe + gamma * Yee
137             
138             Xk = self.__calc_Uk(X0, Kx, self.__ht)
139             Yk = self.__calc_Uk(Y0, Ky, self.__ht)
140             self.__fill_bdyX(Xk)
141             self.__fill_bdyY(Yk)
142             
143             # print(i, numpy.linalg.norm(Xk - X0, numpy.inf), numpy.linalg.norm(Yk - Y0, numpy.inf))
144             if self.__converged(Xk - X0, Yk - Y0, epsilon):
145                 break
146                 
147             X0 = Xk
148             Y0 = Yk
149         else:
150             raise Exception(">>> Not converged after {} iterations! <<<".format(maxIter))
151         
152         return Xk, Yk        
153                 
154                 
155     def __converged(self, deltaX, deltaY, epsilon):
156         normVal1 = numpy.linalg.norm(deltaX, numpy.inf)
157         normVal2 = numpy.linalg.norm(deltaY, numpy.inf)
158         if normVal1 < epsilon and normVal2 < epsilon:
159             return True
160         return False
161         
162         
163     def __calc_Ux(self, U):
164         Ux = numpy.zeros(U.shape)
165         Ux[:, 1:-1] = (U[:, 2:] - U[:, :-2]) / 2
166         return Ux
167         
168         
169     def __calc_Ue(self, U):
170         Ue = numpy.zeros(U.shape)
171         Ue[1:-1, :] = (U[2:, :] - U[:-2, :]) / 2
172         return Ue
173         
174         
175     def __calc_Uxx(self, U):
176         Uxx = numpy.zeros(U.shape)
177         Uxx[:, 1:-1] = U[:, 2:] + U[:, :-2] - 2 * U[:, 1:-1]
178         return Uxx
179         
180         
181     def __calc_Uee(self, U):
182         Uee = numpy.zeros(U.shape)
183         Uee[1:-1, :] = U[2:, :] + U[:-2, :] - 2 * U[1:-1, :]
184         return Uee
185         
186         
187     def __calc_Uxe(self, U):
188         Uxe = numpy.zeros(U.shape)
189         Uxe[1:-1, 1:-1] = (U[2:, 2:] + U[:-2, :-2] - U[:-2, 2:] - U[2:, :-2]) / 4
190         return Uxe
191         
192         
193     def __calc_alpha(self, Xe, Ye):
194         alpha = Xe ** 2 + Ye ** 2
195         return alpha
196         
197         
198     def __calc_beta(self, Xx, Xe, Yx, Ye):
199         beta = Xx * Xe + Yx * Ye
200         return beta
201         
202         
203     def __calc_gamma(self, Xx, Yx):
204         gamma = Xx ** 2 + Yx ** 2
205         return gamma
206         
207         
208     def __calc_Uk(self, U, K, ht):
209         Uk = U + K * ht
210         return Uk
211         
212         
213     def __get_bdy(self):
214         '''
215         获取边界条件
216         '''
217         bdyX = numpy.zeros((self.__n_eta + 1, self.__n_xi + 1))
218         bdyY = numpy.zeros((self.__n_eta + 1, self.__n_xi + 1))
219         
220         for XY, XE in self.__p2c_xi:
221             bdyX[XE[1], XE[0]] = XY[0]
222             bdyY[XE[1], XE[0]] = XY[1]
223             
224         for XY, XE in self.__p2c_eta:
225             bdyX[XE[1], XE[0]] = XY[0]
226             bdyY[XE[1], XE[0]] = XY[1]
227             
228         return bdyX, bdyY
229         
230         
231     def __get_initX(self):
232         '''
233         获取X之初始条件
234         '''
235         X0 = numpy.zeros(self.__bdyX.shape)
236         self.__fill_bdyX(X0)
237         return X0
238         
239         
240     def __get_initY(self):
241         '''
242         获取Y之初始条件
243         '''
244         Y0 = numpy.zeros(self.__bdyY.shape)
245         self.__fill_bdyY(Y0)
246         return Y0
247         
248         
249     def __fill_bdyX(self, U):
250         '''
251         填充X之边界条件
252         '''
253         U[:, 0] = self.__bdyX[:, 0]
254         U[:, -1] = self.__bdyX[:, -1]
255         U[0, :] = self.__bdyX[0, :]
256         U[-1, :] = self.__bdyX[-1, :]
257         
258         
259     def __fill_bdyY(self, U):
260         '''
261         填充Y之边界条件
262         '''
263         U[:, 0] = self.__bdyY[:, 0]
264         U[:, -1] = self.__bdyY[:, -1]
265         U[0, :] = self.__bdyY[0, :]
266         U[-1, :] = self.__bdyY[-1, :]
267     
268         
269     def __get_n(self):
270         arr_xi = numpy.array(list(item[1] for item in self.__p2c_xi))
271         n_xi = numpy.max(arr_xi[:, 0])
272         n_eta = numpy.max(arr_xi[:, 1])
273         return n_xi, n_eta
274         
275         
276 class EGPlot(object):
277     
278     @staticmethod
279     def plot_fig(egObj):
280         maxIter = 1000000
281         epsilon = 1.e-9
282         
283         X, Y = egObj.get_solu(maxIter, epsilon)
284         
285         fig = plt.figure(figsize=(6, 4))
286         ax1 = plt.subplot()
287         
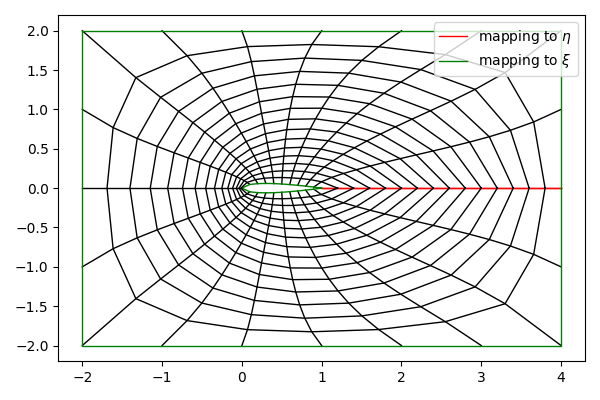
288         ax1.plot(X[:, 0], Y[:, 0], c="red", lw=1, label="mapping to $\\eta$")
289         ax1.plot(X[:, -1], Y[:, -1], c="red", lw=1)
290         n_eta, n_xi = X.shape
291         for colIdx in range(1, n_xi-1):
292             tmpX = X[:, colIdx]
293             tmpY = Y[:, colIdx]
294             ax1.plot(tmpX, tmpY, "k-", lw=1)
295             
296         ax1.plot(X[0, :], Y[0, :], c="green", lw=1, label="mapping to $\\xi$")
297         ax1.plot(X[-1, :], Y[-1, :], c="green", lw=1)
298         for rowIdx in range(1, n_eta-1):
299             tmpX = X[rowIdx, :]
300             tmpY = Y[rowIdx, :]
301             ax1.plot(tmpX, tmpY, "k-", lw=1)
302         ax1.legend()
303         
304         fig.tight_layout()
305         fig.savefig("plot_fig.png", dpi=100)
306 
307 
308 
309 if __name__ == "__main__":
310     p2c_xi, p2c_eta = build_bdy_maps()
311     egObj = EllipticGrid(p2c_xi, p2c_eta)
312     
313     EGPlot.plot_fig(egObj)
    View Code
  • 结果展示
     
    左图为翼型所处物理空间, 右图为利用椭圆型方程在此物理空间生成之网格. 图中绿色与红色曲线分别映射至计算空间相应边界.
  • 使用建议
    ①. 时间步长$h_t$选择过小收敛速度慢, 选择过大容易发散;
    ②. 物理空间与计算空间边界映射关系可灵活选择;
    ③. 多连通物理空间需适当剖分转单连通空间.
  • 参考文档
    Thompson, Joe F., Zahir UA Warsi, and C. Wayne Mastin. Numerical grid generation: foundations and applications. Elsevier North-Holland, Inc., 1985.

 

posted @ 2021-08-16 22:34  LOGAN_XIONG  阅读(2468)  评论(1)    收藏  举报