AtCoder Beginner Contest 042 题解

🌸欢迎来到我的算法小屋🌸

前言

写大体感觉，总结，文章写完之后补充。

	Task Name
A	Iroha and Haiku (ABC Edition)
B	Iroha Loves Strings (ABC Edition)
C	Iroha's Obsession
D	Iroha and a Grid

A

题目描述

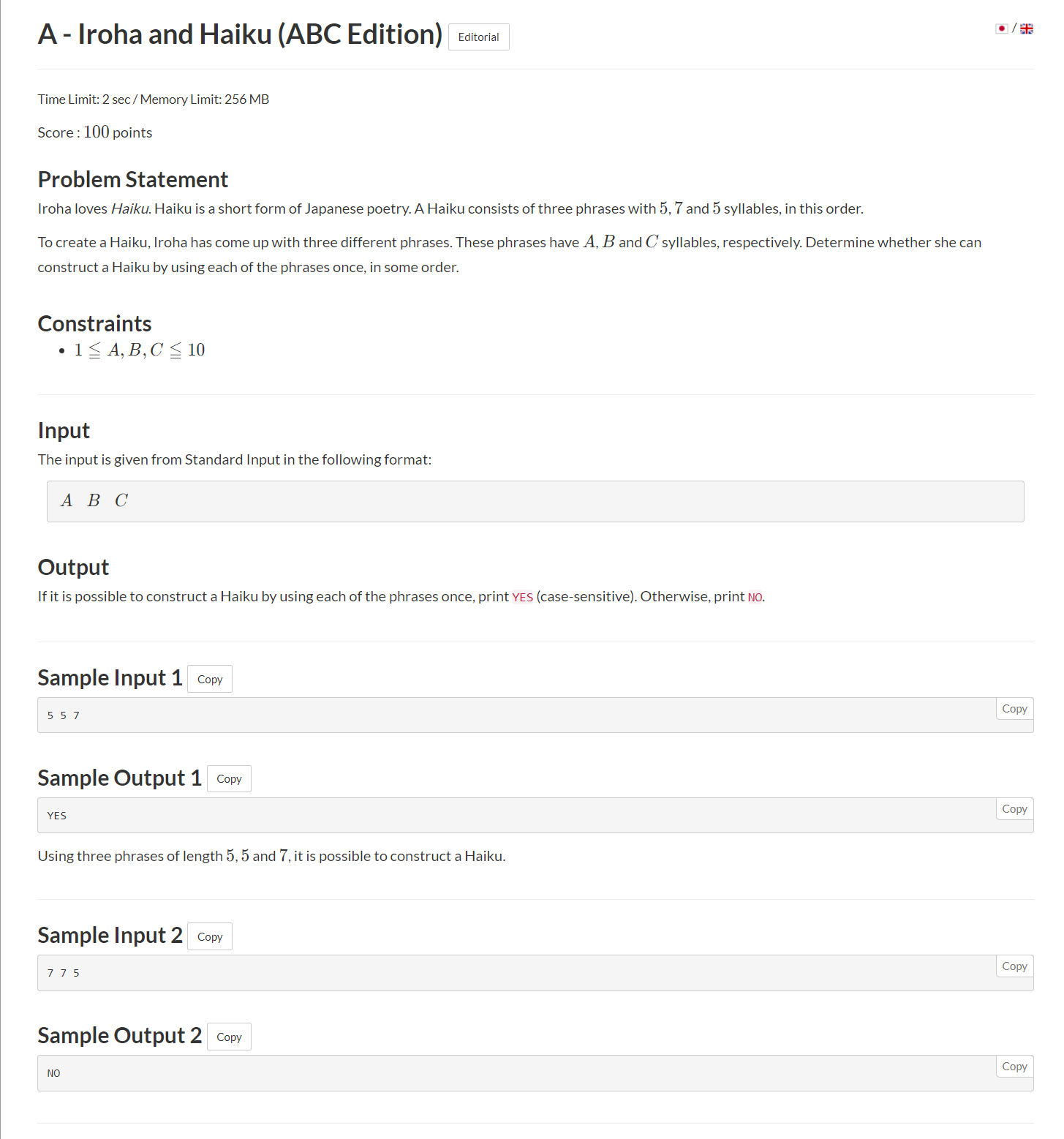
题目大意如下：

输入三个数，假如输入的三个数中有两个5，一个7，那么就符合要求，其他的都不行

解题报告

A是签到水题，可以数组模拟哈希表，也可以循环去统计5和7的个数

参考代码(C++)

/*
伊吕波喜欢俳句。俳句是日本诗歌的一种缩写形式。
俳句由 5、7 和 5 个音节的三个短语组成，按此顺序排列。
为了创造俳句，Iroha 提出了三个不同的短语。这些短语分别有 A、B 和 C 音节。
确定她是否可以按某种顺序使用每个短语一次来构建俳句。
*/

#include<bits/stdc++.h>

using namespace std;

#define INF 0x3f3f3f3f
#define N 520
#define mem(a,b) memset(a,b,sizeof(a))
typedef long long LL;
int n;
int a[3],h[10];

void run(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
}

inline int read(){ 
    int x=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=(x<<1)+(x<<3)+(c^48);
        c=getchar();
    } 
    return x*f;
}


int main(){
    run();

    for(int i = 0;i < 3;i++){
         cin >> a[i];
         h[a[i]] ++;
    }

    if(h[5] == 2 && h[7] == 1) puts("YES");
    else puts("NO");

    return 0;
}

要点总结

练打字速度的了....

B

题目描述

题目大意如下：

给咱们N个字符串，让我们输出这N个字符串按照字典序产生的最终序列。

解题报告

先普及一下字典序的知识吧。

其实也不用想得特别晦涩难懂，因为abcd..xyz的升序，在ASCII码上也是从小到大的升序，那么string + sort函数的方式就挺简约了。

参考代码(C++)

/*
连接给定的字符串，产生长的字符串
*/

#include<bits/stdc++.h>

using namespace std;

#define INF 0x3f3f3f3f
#define N 520
#define mem(a,b) memset(a,b,sizeof(a))
typedef long long LL;
int T;
std::vector<string> v;

void run(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
}

inline int read(){ 
    int x=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=(x<<1)+(x<<3)+(c^48);
        c=getchar();
    } 
    return x*f;
}


int main(){
    run();

    int n,k;
    cin >> n >> k;
       while(n--){
           string str;
           cin >> str;
           v.push_back(str);
       }

       sort(v.begin(),v.end());

       for(auto it: v){
           cout <<it;
       }
    return 0;
}

要点总结

stl还是蛮香的..

C

题目描述

、

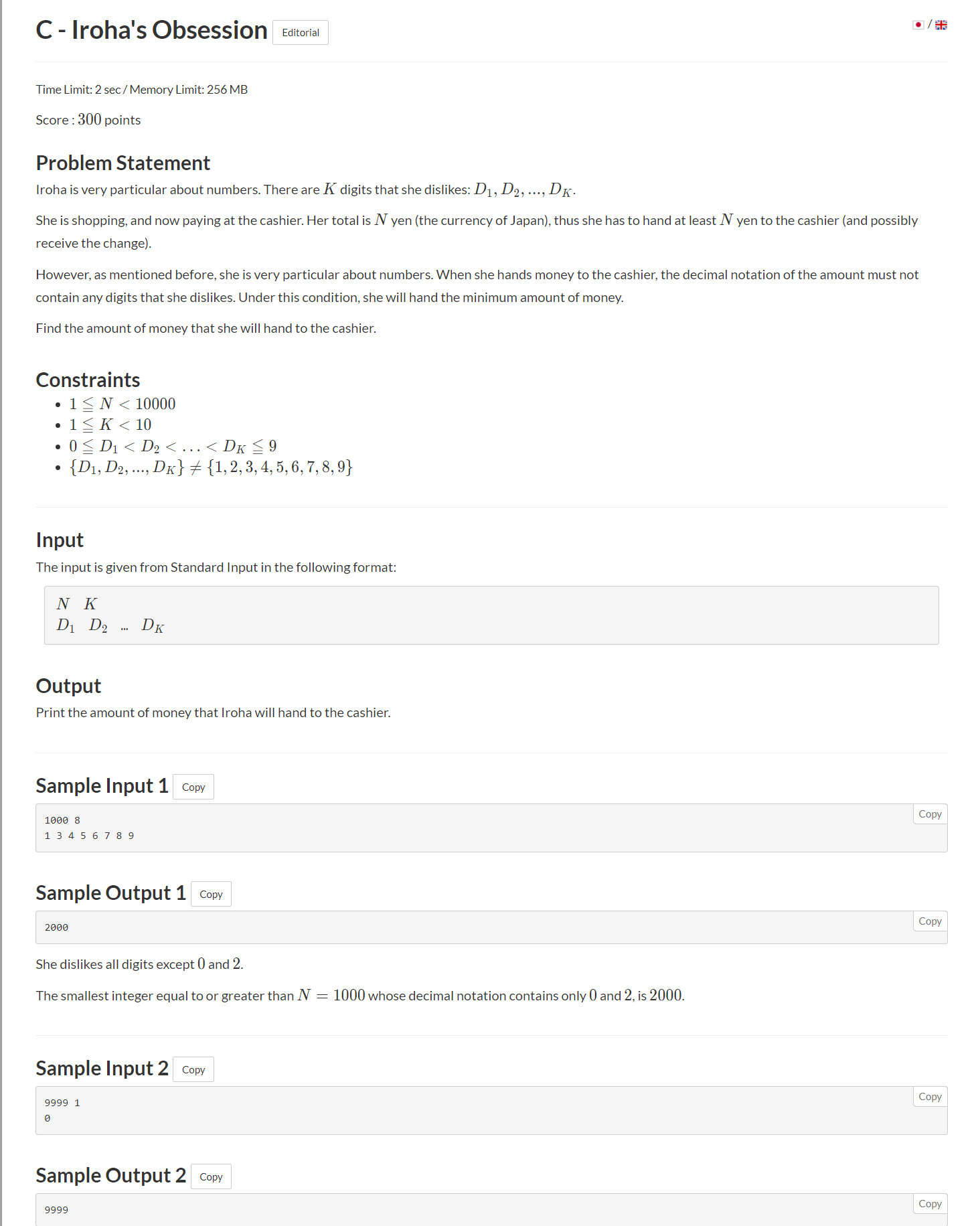题目大意是让咱们找到一个数字，这个数字里面不包含这个人罗列出来的，它讨厌的这些数字。

解题报告

可以直接枚举，然后通过while + 取模运算符 + 整数除法来逐一判断每一位是否包含这人讨厌的数字，枚举到第一个完全由ta不讨厌的数字组成的整数的时候，就可以跳出枚举，输出结果了。

参考代码(C++)

#include<bits/stdc++.h>

using namespace std;

#define INF 0x3f3f3f3f
#define D 15
#define mem(a,b) memset(a,b,sizeof(a))
typedef long long LL;
int n,k;
int h[D];

void run(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
}

inline int read(){ 
    int x=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=(x<<1)+(x<<3)+(c^48);
        c=getchar();
    } 
    return x*f;
}


int main(){
    run();

    cin >> n >> k;
    mem(h,0);

       for(int i = 1;i <= k;i++){
           int x;
           cin >>x;
           h[x] ++;
       }

       //题目中的N是限制，不是金额的限制
       for(int i = n; ;i++){
           int x  = i;
           bool dislike = false;
           while(x){
               if(h[x%10] == 0){
                   x/=10;
               }else{
                   dislike = true;
                   break;
               }
           }
           if(!dislike) {
               cout <<i<<'\n';
               break;
           }else continue;
       }


    return 0;
}

要点总结

暂无

D

题目描述

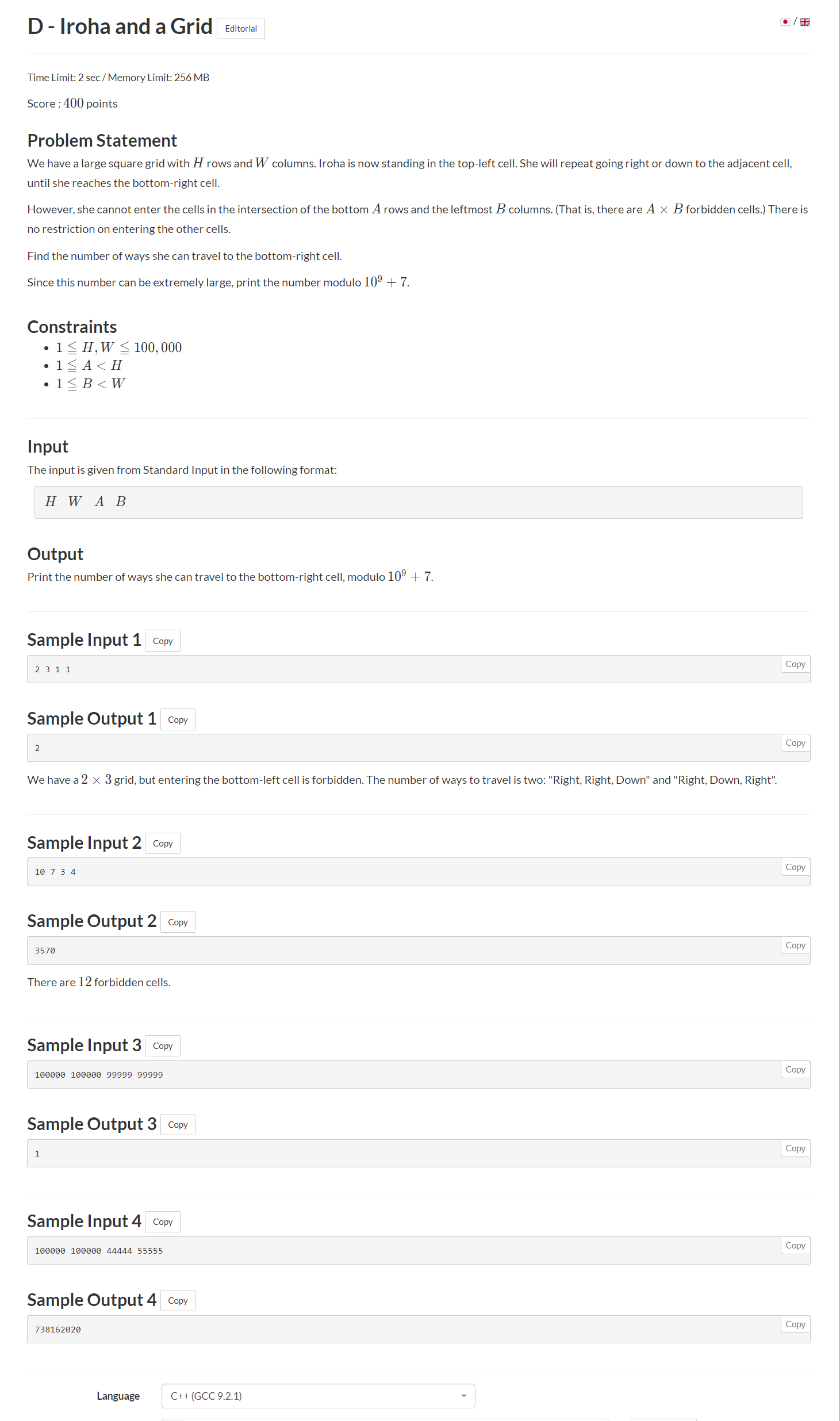
题目大意：

给了咱们一个高H宽W的方格，现在咱们的位置在左上角（ Iroha is now standing in the top-left cell.），

咱们只能向下或者向右走，需要咱们走到右下角(she reaches the bottom-right cell.)。

但是在左下角的那片区域是不能通过的（ bottom rows and the leftmost columns）

现在问，咱们走到右下角的终点的方案一共有多少种（Find the number of ways she can travel to the bottom-right cell.）

解决报告

问咱们一共有多少种方案，以及提示说最后的结果很大，特别是看到十万的数据范围，然后需要取模的时候，其实就可以向着组合数学的方向思考了。因为当前每走的一个格子，都是一种选择方案。

本题主要的思路是参考这位大佬的：

(AtCoder - 1974)いろはちゃんとマス目 / Iroha and a Grid(乘法逆元+组合计数)

我的代码可能思路更加清晰一点，仅供参考

参考代码(C++)

#include <bits/stdc++.h>

using namespace std; 
/*宏定义*/
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define PI 3.141592653589793238462
#define N 100010
#define mem(a,b) memset(a,b,sizeof(a))
#define x first
#define y second

typedef long long ll;
const double eps = 1e-8;
int t,n;

/*
* 常用函数
*/

//最大公约数
ll gcd(ll a,ll b) {return b==0 ? a : gcd(b,a%b);}
//最小公倍数
ll lcm(ll a,ll b) {return a*b / gcd(a,b);}
//lowbit运算
int lowbit(int x) {return x & (-x);}
//快速幂 a的b次，取mod
ll qmi(ll a,ll b,ll mod) {
    ll ans = 1;
    while(b) {
        if(b & 1) ans = ans * a % mod;
        a = a * a % mod;
        b >>= 1; 
    } 
    return ans;
}
//组合数学的初始化阶乘数组
ll fact[N];
void init_fact(){
    fact[0] = 1;
    for(int i = 1; i < N;i++){
        fact[i] = 1ll*fact[i-1]*i % MOD;
    }
}

//计算乘法逆元 —— 公式
ll inverse(ll a){
    return qmi(a,MOD-2,MOD);
}

//计算组合数 —— 组合数的公式，分式部分用乘法逆元表示
ll C(ll n,ll m){
    return(1ll * fact[n] * inverse(fact[m]) % MOD)* inverse(fact[n-m])%MOD;
}

//cin 、 cout 优化
void run(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
}

//快读
inline int read(){ 
    int x=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=(x<<1)+(x<<3)+(c^48);
        c=getchar();
    } 
    return x*f;
}


int main(){
    run();
    int h,w,a,b;
    cin >> h >> w >> a >> b;
    ll ans = 0;
    init_fact();

    //b是左下角不能走的区域的边长，w是整体的下边长
    for(int i = b+1;i <=w;i++){
        ans = (ans+C(h-a+i-2,h-a-1)*C(w+a-i-1,a-1)%MOD)%MOD;
    }   

    cout << ans;
    return 0;
}

要点总结

在组合数中，首先要清楚组合数的公式是这种的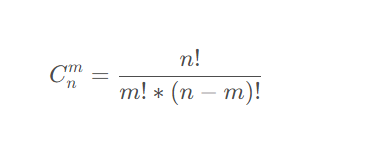，，因为整数除法会出现精确缺失的清楚，因此要结合费马小定理来求乘法逆元，最后就可以化除法为乘法。

posted @ 2022-08-11 21:17 xxdjx 阅读(104) 评论(0) 收藏举报

刷新页面返回顶部

xxdjx

AtCoder Beginner Contest 042 题解

前言

A

题目描述

解题报告

参考代码(C++)

要点总结

B

题目描述

解题报告

参考代码(C++)

要点总结

C

题目描述

解题报告

参考代码(C++)

要点总结

D

题目描述

解决报告

参考代码(C++)

要点总结

公告