第3周_作业题_1层隐藏层的神经网络分类二维数据
1层隐藏层的神经网络分类二维数据¶
1. 导入包¶
① numpy是Python科学计算的基本包。
② sklearn提供了用于数据挖掘和分析的简单有效的工具。
③ matplotlib是在Python中常用的绘制图形的库。
④ testCases提供了一些测试示例用以评估函数的正确性。
⑤ planar_utils提供了此作业中使用的各种函数。
In [2]:
import sys
import numpy
import matplotlib
import sklearn #安装 pip install scikit-learn
print(sys.version) # 打印 python 版本号
print(numpy.__version__) # 打印 numpy 包 版本号
print(matplotlib.__version__) # 打印 matplotlib 包 版本号
print(sklearn.__version__) # 打印 h5py 包 版本号
3.12.4 (tags/v3.12.4:8e8a4ba, Jun 6 2024, 19:30:16) [MSC v.1940 64 bit (AMD64)]
2.2.3
3.10.1
1.6.1
需要的文件
需要的testCases.py和planar_utils.py文件下载链接:
下载:https://wwyy.lanzouu.com/iekB72wste9a 密码:htp0
In [128]:
# Package imports
import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
%matplotlib inline
# 设置一个固定的随机种子,以保证接下来的步骤中我们的结果是一致的。
np.random.seed(1)
2. 数据集¶
2.1 导入数据集¶
① 首先,让我们获取要使用的数据集。
② 以下代码会将花的图案的2类数据集加载到变量X和Y中。
In [129]:
X, Y = load_planar_dataset()
2.2 查看数据集图案¶
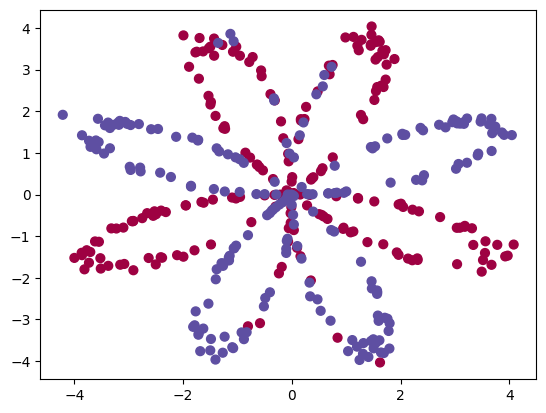
① 把数据集加载完成了,然后使用matplotlib可视化数据集。
② 数据看起来像一朵由红色(y = 0)和蓝色(y = 1)的数据点组成的花朵图案。
③ 我们的目标是建立一个适合该数据的分类模型。
In [130]:
# 绘制散点图
plt.scatter(X[0, :], X[1, :], c=Y.reshape(X[0,:].shape), s=40, cmap=plt.cm.Spectral)
Out[130]:
<matplotlib.collections.PathCollection at 0x24af4ea8ce0>
2.3 查看数据集维度¶
① 现在,我们已经有了以下的东西:
- X:一个numpy的矩阵,包含了这些数据点的数值
- Y:一个numpy的向量,对应着的是X的标签【0 | 1】(红色:0 , 蓝色 :1)
② 我们继续来仔细地看数据。
In [131]:
shape_X = X.shape
shape_Y = Y.shape
m = shape_X[1] # 训练集里面的数量
print ('X的维度为: ' + str(shape_X))
print ('Y的维度为: ' + str(shape_Y))
print ("数据集里面的数据有:" + str(m) + " 个")
X的维度为: (2, 400)
Y的维度为: (1, 400)
数据集里面的数据有:400 个
3. Logistic回归¶
3.1 Logistic回归简介¶
① 在构建完整的神经网络之前,先让我们看看逻辑回归在这个问题上的表现如何。
② 我们可以使用sklearn的内置函数来做到这一点, 运行下面的代码来训练数据集上的逻辑回归分类器。
3.2 Logistic回归模型¶
In [133]:
# Train the logistic regression classifier
clf = sklearn.linear_model.LogisticRegressionCV();
# clf.fit(X.T, Y.T); #这个会报错
clf.fit(X.T, Y.T.ravel()); # 或 Y.T.flatten()
代码解释:
sklearn.linear_model.LogisticRegressionCV()
- 这是 scikit-learn 库中用于逻辑回归的类,带有交叉验证功能。
- LogisticRegressionCV 是逻辑回归分类器的实现,它会通过交叉验证自动选择最佳的正则化参数(如 L1 或 L2 正则化)。
- clf 是这个分类器的实例。
clf.fit(X.T, Y.T.ravel())
- clf.fit 是逻辑回归分类器的训练方法,用于拟合模型。
- X.T 和 Y.T 是数据矩阵 X 和目标向量 Y 的转置。
- Y.T.ravel() 是对 Y.T 进行处理,将其从列向量(二维数组)转换为一维数组。
3.3 绘制边界¶
① 现在,你可以运行下面的代码以绘制此模型的决策边界:
相关知识
1. NumPy 的形状问题
- Y 和 LR_predictions 的形状必须是一致的,并且是一维数组(形状为 (n_samples,))。
- 如果 Y 是一个二维数组(形状为 (n_samples, 1)),需要将其转换为一维数组。
2. 计算准确性的公式
准确性公式是:
在代码中,np.dot(Y, LR_predictions) 和 np.dot(1 - Y, 1 - LR_predictions) 的结果应该是一个标量,表示正确预测的数量。
3. NumPy 的 np.dot
np.dot 用于计算两个数组的点积。
- 如果输入是一维数组,结果是一个标量。
- 如果输入是二维数组,结果是一个数组。
4. NumPy 的 np.mean
- np.mean 用于计算数组的均值。
- 可以用它来计算准确率,因为准确率本质上是正确预测的比例。
In [135]:
# Plot the decision boundary for logistic regression
# 绘制决策边界
plot_decision_boundary(lambda x: clf.predict(x), X, Y)
# 图标题
plt.title("Logistic Regression")
# 打印准确性
LR_predictions = clf.predict(X.T)
# LR_predictions = clf.predict(X.T).ravel() #展平为一维数组
Y = Y.ravel() #展平为一维数组
print ('逻辑回归的准确性:%d ' % float((np.dot(Y,LR_predictions) + np.dot(1-Y,1-LR_predictions))/float(Y.size)*100) +
'% ' + "(正确标记的数据点所占的百分比)")
逻辑回归的准确性:47 % (正确标记的数据点所占的百分比)
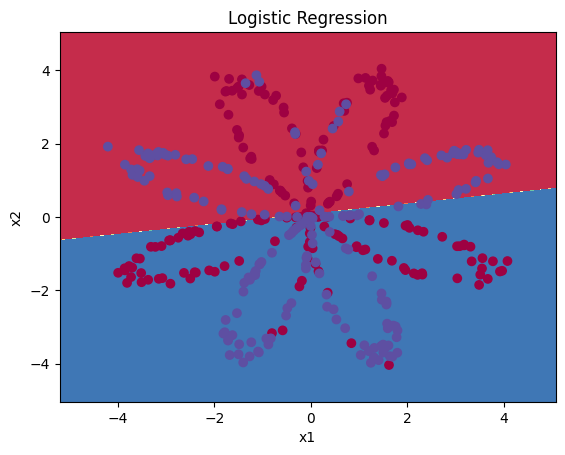
② 由于数据集不是线性可分类的,因此逻辑回归效果不佳。让我们试试是否神经网络会做得更好吧!
4. 神经网络模型¶
4.1 神经网络简介¶
① 从上面我们可以得知Logistic回归不适用于“flower数据集”。
② 现在你将训练带有单个隐藏层的神经网络。
③ 这是我们的模型:
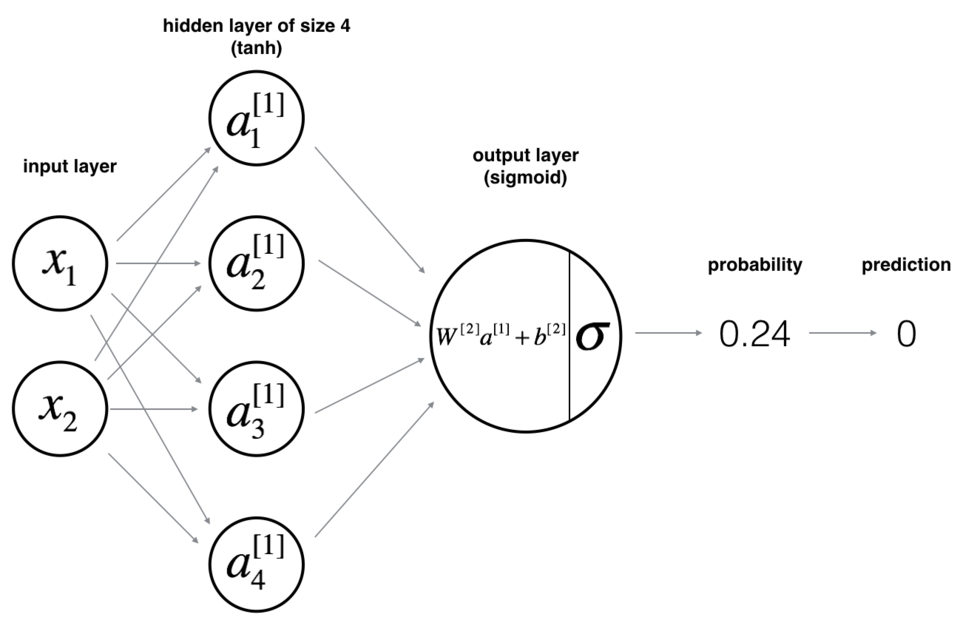
4.2 神经网络数学模型¶
① 数学原理:
例如对第\(i\)个样本\(x^{(i)}\),执行以下操作:
- \(z^{[1] (i)} = W^{[1]} x^{(i)} + b^{[1] (i)}\tag{1}\)
- \(a^{[1] (i)} = \tanh(z^{[1] (i)})\tag{2}\)
- \(z^{[2] (i)} = W^{[2]} a^{[1] (i)} + b^{[2] (i)}\tag{3}\)
- \(\hat{y}^{(i)} = a^{[2] (i)} = \sigma(z^{ [2] (i)})\tag{4}\)
- \(y^{(i)}\_{prediction} = \begin{cases} 1 & \mbox{if } a^{[2](i)} > 0.5 \\ 0 & \mbox{otherwise } \end{cases}\tag{5}\)
② 根据所有的预测数据,你还可以如下计算损失J:
\(J = - \frac{1}{m} \sum\limits\_{i = 0}^{m} \large\left(\small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large \right) \small \tag{6}\)
4.3 建立神经网络方法¶
① 建立神经网络的一般方法是:
- 定义神经网络结构(输入单元数,隐藏单元数等)。
- 初始化模型的参数
- 循环:
- 3.1 实施前项传播
- 3.2 计算损失
- 3.3 实现后向传播
- 3.4 更新参数(梯度下降)
② 我们通常会构建辅助函数来计算第(1)-(3)步,然后将它们合并为nn_model()函数。
③ 一旦构建了 nn_model() 并学习了正确的参数,就可以对新数据进行预测。
4.4 定义神经网络结构¶
① 在构建神经网络之前,我们要先把神经网络的结构给定义好。
② 定义三个变量:
- n_x:输入层的大小
- n_h:隐藏层的大小(将其设置为4)
- n_y:输出层的大小
note:使用shape来找到n_x和n_y。 另外,将隐藏层大小硬编码为4。
In [136]:
def layer_sizes(X, Y):
"""
参数:
X - 输入数据集,维度为(输入的数量,训练/测试的数量)
Y - 标签,维度为(输出的数量,训练/测试数量)
返回:
n_x - 输入层的数量
n_h - 隐藏层的数量
n_y - 输出层的数量
"""
# 输入层大小
n_x = X.shape[0]
# 隐藏层大小
n_h = 4
# 输出层大小
n_y = Y.shape[0]
return (n_x, n_h, n_y)
In [137]:
# 测试一下 layer_sizes 函数
print("=========================测试layer_sizes=========================")
X_assess, Y_assess = layer_sizes_test_case()
(n_x, n_h, n_y) = layer_sizes(X_assess, Y_assess)
print("The size of the input layer is: n_x = " + str(n_x))
print("The size of the hidden layer is: n_h = " + str(n_h))
print("The size of the output layer is: n_y = " + str(n_y))
=========================测试layer_sizes=========================
The size of the input layer is: n_x = 5
The size of the hidden layer is: n_h = 4
The size of the output layer is: n_y = 2
4.5 初始化模型的参数¶
① 在这里,我们要实现函数initialize_parameters()。
② 我们要确保我们的参数大小合适。
③ 我们将会用随机值初始化权重矩阵。
- np.random.randn(a,b) * 0.01来随机初始化一个维度为(a,b)的矩阵。
- np.zeros((a,b))用零初始化矩阵(a,b)。将偏向量初始化为零。
In [138]:
def initialize_parameters(n_x, n_h, n_y):
"""
参数:
n_x - 输入层节点的数量
n_h - 隐藏层节点的数量
n_y - 输出层节点的数量
返回:
parameters - 包含参数的字典:
W1 - 权重矩阵,维度为(n_h,n_x)
b1 - 偏向量,维度为(n_h,1)
W2 - 权重矩阵,维度为(n_y,n_h)
b2 - 偏向量,维度为(n_y,1)
"""
# 设置一个种子,这样你的输出与我们的匹配,尽管初始化是随机的。
np.random.seed(2)
W1 = np.random.randn(n_h,n_x) * 0.01
b1 = np.zeros((n_h,1))
W2 = np.random.randn(n_y,n_h) * 0.01
b2 = np.zeros((n_y,1))
# 使用断言确保我的数据格式是正确的
assert(W1.shape == ( n_h , n_x ))
assert(b1.shape == ( n_h , 1 ))
assert(W2.shape == ( n_y , n_h ))
assert(b2.shape == ( n_y , 1 ))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
In [139]:
#测试一下 initialize_parameters 函数
print("=========================测试initialize_parameters=========================")
n_x, n_h, n_y = initialize_parameters_test_case()
parameters = initialize_parameters(n_x, n_h, n_y)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
=========================测试initialize_parameters=========================
W1 = [[-0.00416758 -0.00056267]
[-0.02136196 0.01640271]
[-0.01793436 -0.00841747]
[ 0.00502881 -0.01245288]]
b1 = [[0.]
[0.]
[0.]
[0.]]
W2 = [[-0.01057952 -0.00909008 0.00551454 0.02292208]]
b2 = [[0.]]
4.6 循环¶
4.6.1 前向传播¶
① 我们现在要实现前向传播函数forward_propagation()。
② 我们可以使用sigmoid()函数,也可以使用np.tanh()函数。
③ 步骤如下:
- 使用字典类型的parameters(它是initialize_parameters() 的输出)检索每个参数。
- 实现前向传播,计算\(Z^{[1]}, A^{[1]}, Z^{[2]}\)和\(A^{[2]}\)(所有训练数据的预测结果向量)。
- 反向传播所需的值存储在cache中,cache将作为反向传播函数的输入。
步骤及相关解释
1. 前向传播(Forward Propagation)
前向传播是神经网络中从输入层到输出层的计算过程。它包括以下步骤:
- 输入层:接收输入数据。
- 隐藏层:对输入数据进行加权求和和非线性变换。
- 输出层:生成最终的预测结果。
在前向传播中,每个神经元的输出可以表示为:
其中:
- ( Z ) 是加权输入。
- ( W ) 是权重矩阵。
- ( X ) 是输入数据。
- ( b ) 是偏置项。
- ( g ) 是激活函数(如 Sigmoid、ReLU 等)。
- ( A ) 是激活后的输出。
2. 缓存(Cache)
在神经网络的实现中,cache 是一个字典,用于存储中间计算结果。这些结果在反向传播中会被用到。例如:
Z1:第一个隐藏层的加权输入。A1:第一个隐藏层的激活输出。Z2:输出层的加权输入。A2:输出层的激活输出。
3. 测试用例(Test Case)
forward_propagation_test_case() 是一个测试函数,用于生成测试数据:
X_assess:测试输入数据。parameters:测试模型的参数(包括权重和偏置)。
这些测试数据用于验证 forward_propagation 函数的正确性。
4. NumPy 的 np.mean
np.mean 用于计算数组的均值。在这段代码中,np.mean 被用来计算 cache 中各个变量的均值,以便验证输出是否与预期一致。
5. 打印结果
通过打印 cache 中各个变量的均值,可以直观地检查 forward_propagation 函数的输出是否正确。
In [171]:
def forward_propagation(X, parameters):
"""
参数:
X - 维度为(n_x,m)的输入数据。
parameters - 初始化函数(initialize_parameters)的输出
返回:
A2 - 使用sigmoid()函数计算的第二次激活后的数值
cache - 包含“Z1”,“A1”,“Z2”和“A2”的字典类型变量
"""
# 从字典 “parameters” 中检索每个参数
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# 实现前向传播计算A2(概率)
Z1 = np.dot(W1,X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2,A1) + b2
A2 = sigmoid(Z2)
# 确保 A2 的形状为 (1, n_samples)
A2 = A2.reshape(1, -1)
#使用断言确保我的数据格式是正确的
assert(A2.shape == (1,X.shape[1]))
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache
In [141]:
# 测试一下 forward_propagation 函数
print("=========================测试forward_propagation=========================")
X_assess, parameters = forward_propagation_test_case()
A2, cache = forward_propagation(X_assess, parameters)
# 我们在这里使用均值只是为了确保你的输出与我们的输出匹配。
print(np.mean(cache['Z1']) ,np.mean(cache['A1']),np.mean(cache['Z2']),np.mean(cache['A2']))
=========================测试forward_propagation=========================
-0.0004997557777419913 -0.000496963353231779 0.00043818745095914653 0.500109546852431
4.6.2 计算成本¶
① 现在,我们已经计算了\(A^{[2]}\)
② \(a^{[2](i)}\)包含了训练集里每个数值,现在我们可以构建成本函数了。
③ 我们的成本选择交叉熵损失,计算成本的公式如下:
\(J = - \frac{1}{m} \sum\limits\_{i = 0}^{m} \large{(} \small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large{)} \small\tag{7}\)
In [142]:
def compute_cost(A2, Y, parameters):
"""
计算方程(7)中给出的交叉熵成本,
参数:
A2 - 使用sigmoid()函数计算的第二次激活后的数值
Y - "True"标签向量,维度为(1,数量)
parameters - 一个包含W1,B1,W2和B2的字典类型的变量
返回:
成本 - 交叉熵成本给出方程(7)
"""
# 样本数量
m = Y.shape[1]
# 计算交叉熵代价
epsilon = 1e-5 # 一个非常小的值
logprobs = Y * np.log(A2 + epsilon) + (1 - Y) * np.log(1 - A2 + epsilon) #防止为0
# logprobs = Y*np.log(A2) + (1-Y)* np.log(1-A2)
cost = -1/m * np.sum(logprobs)
# 确保损失是我们期望的维度
# 例如,turns [[17]] into 17
cost = np.squeeze(cost)
assert(isinstance(cost, float))
return cost
In [143]:
# 测试一下 compute_cost 函数
print("=========================测试compute_cost=========================")
A2, Y_assess, parameters = compute_cost_test_case()
print("cost = " + str(compute_cost(A2, Y_assess, parameters)))
=========================测试compute_cost=========================
cost = 0.6928998985200261
① 使用正向传播期间计算的cache,现在可以利用它实现反向传播。
② 现在我们要开始实现函数backward_propagation()。
4.6.3 后向传播¶
① 反向传播通常是深度学习中最难(数学意义)部分,为了帮助你,这里有反向传播讲座的幻灯片。
② 由于我们正在构建向量化实现,因此我们将需要使用这下面的六个方程:

③ 要计算\(dz^{[1]}\),你首先需要计算\(g^{[1]'}(Z^{[1]})\)。
④ \(g^{[1]}(...)\) 是tanh激活函数,因此如果\(a = g^{[1]}(z)\)则\(g^{[1]'}(z) = 1-a^2\)。
⑤ 所以我们需要使用(1 - np.power(A1, 2))计算\(g^{[1]'}(Z^{[1]})\)。
In [144]:
def backward_propagation(parameters, cache, X, Y):
"""
使用上述说明搭建反向传播函数。
参数:
parameters - 包含我们的参数的一个字典类型的变量。
cache - 包含“Z1”,“A1”,“Z2”和“A2”的字典类型的变量。
X - 输入数据,维度为(2,数量)
Y - “True”标签,维度为(1,数量)
返回:
grads - 包含W和b的导数一个字典类型的变量。
"""
m = X.shape[1]
# 首先,从字典“parameters”中检索W1和W2。
W1 = parameters["W1"]
W2 = parameters["W2"]
# 还可以从字典“cache”中检索A1和A2。
A1 = cache["A1"]
A2 = cache["A2"]
# 反向传播:计算 dW1、db1、dW2、db2。
dZ2= A2 - Y
dW2 = 1 / m * np.dot(dZ2,A1.T)
db2 = 1 / m * np.sum(dZ2,axis=1,keepdims=True)
dZ1 = np.dot(W2.T,dZ2) * (1-np.power(A1,2))
dW1 = 1 / m * np.dot(dZ1,X.T)
db1 = 1 / m * np.sum(dZ1,axis=1,keepdims=True)
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads
In [145]:
# 测试一下 backward_propagation 函数
print("=========================测试backward_propagation=========================")
parameters, cache, X_assess, Y_assess = backward_propagation_test_case()
grads = backward_propagation(parameters, cache, X_assess, Y_assess)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("db2 = "+ str(grads["db2"]))
=========================测试backward_propagation=========================
dW1 = [[ 0.01018708 -0.00708701]
[ 0.00873447 -0.0060768 ]
[-0.00530847 0.00369379]
[-0.02206365 0.01535126]]
db1 = [[-0.00069728]
[-0.00060606]
[ 0.000364 ]
[ 0.00151207]]
dW2 = [[ 0.00363613 0.03153604 0.01162914 -0.01318316]]
db2 = [[0.06589489]]
⑥ 反向传播完成了,我们开始对参数进行更新。
4.6.4 更新参数¶
① 我们需要使用(dW1,db1,dW2,db2)更新(W1,b1,W2,b2)。
② 更新算法如下:
$ \theta = \theta - \alpha \frac{\partial J }{ \partial \theta }$
③ 其中:
- \(\alpha\) 代表学习率
- \(\theta\) 代表一个参数。
④ 我们需要选择一个良好的学习速率,我们可以看一下下面这两个图(图由Adam Harley提供)。
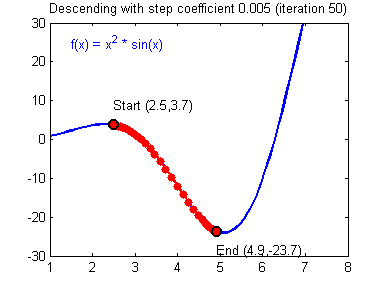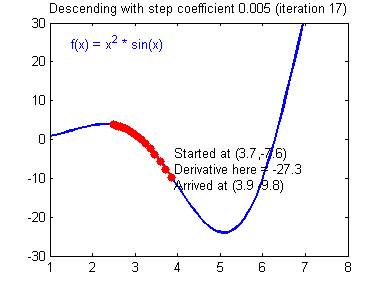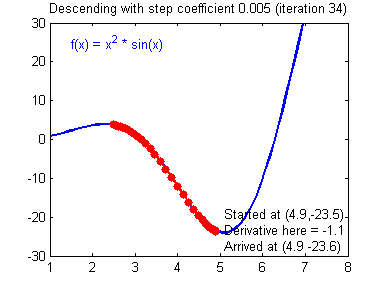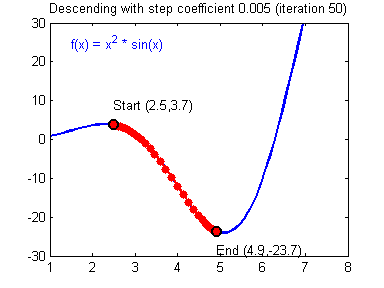
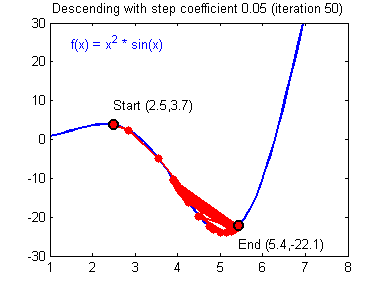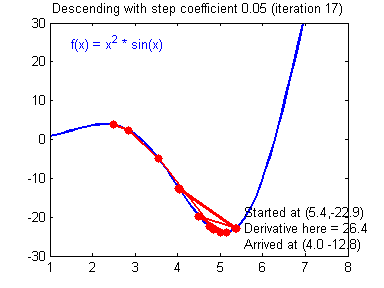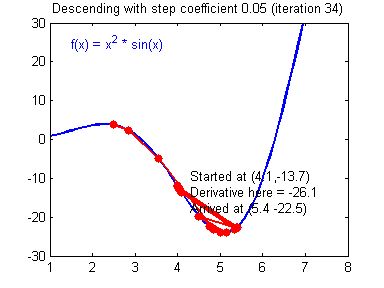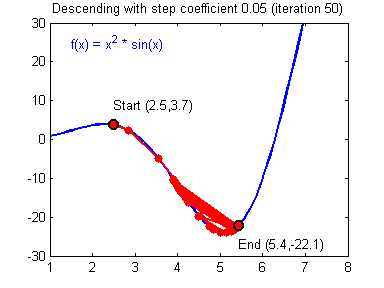
⑤ 上面两个图分别代表了具有良好学习速率(收敛)和不良学习速率(发散)的梯度下降算法。
In [146]:
def update_parameters(parameters, grads, learning_rate = 1.2):
"""
使用上面给出的梯度下降更新规则更新参数
参数:
parameters - 包含参数的字典类型的变量。
grads - 包含导数值的字典类型的变量。
learning_rate - 学习速率
返回:
parameters - 包含更新参数的字典类型的变量。
"""
# 从字典“parameters”中检索每个参数
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# 从字典“梯度”中检索每个梯度
dW1 = grads["dW1"]
db1 = grads["db1"]
dW2 = grads["dW2"]
db2 = grads["db2"]
# 每个参数的更新规则
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
In [147]:
# 测试一下 update_parameters 函数
print("=========================测试update_parameters=========================")
parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
=========================测试update_parameters=========================
W1 = [[-0.00643025 0.01936718]
[-0.02410458 0.03978052]
[-0.01653973 -0.02096177]
[ 0.01046864 -0.05990141]]
b1 = [[-1.02420756e-06]
[ 1.27373948e-05]
[ 8.32996807e-07]
[-3.20136836e-06]]
W2 = [[-0.01041081 -0.04463285 0.01758031 0.04747113]]
b2 = [[0.00010457]]
4.7 整合¶
① 我们现在把上面的东西整合到nn_model()中,神经网络模型必须以正确的顺序使用先前的功能。
In [208]:
def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):
"""
参数:
X - 数据集,维度为(2,示例数)
Y - 标签,维度为(1,示例数)
n_h - 隐藏层的数量
num_iterations - 梯度下降循环中的迭代次数
print_cost - 如果为True,则每1000次迭代打印一次成本数值
返回:
parameters - 模型学习的参数,它们可以用来进行预测。
"""
# 初始化参数,然后检索 W1, b1, W2, b2。输入:“n_x, n_h, n_y”。
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
# 初始化参数,然后检索 W1, b1, W2, b2。
# 输入:“n_x, n_h, n_y”。输出=“W1, b1, W2, b2,参数”。
parameters = initialize_parameters(n_x, n_h, n_y)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# 循环(梯度下降)
for i in range(0, num_iterations):
# 前项传播
A2, cache = forward_propagation(X, parameters)
# 计算成本
cost = compute_cost(A2, Y, parameters)
# 反向传播
grads = backward_propagation(parameters, cache, X, Y)
# 更新参数
parameters = update_parameters(parameters, grads)
# 每1000次迭代打印成本
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
return parameters
In [210]:
# 测试一下 nn_model 函数
print("=========================测试nn_model=========================")
X_assess, Y_assess = nn_model_test_case()
parameters = nn_model(X_assess, Y_assess, 4, num_iterations=10000, print_cost=False)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
=========================测试nn_model=========================
C:\Users\86158\AppData\Local\Temp\ipykernel_10044\499126413.py:10: RuntimeWarning: divide by zero encountered in log
logprobs = np.multiply(np.log(A2), Y) + np.multiply(np.log(1 - A2), (1 - Y))
C:\Users\86158\AppData\Local\Temp\ipykernel_10044\499126413.py:6: RuntimeWarning: overflow encountered in exp
return 1/(1+np.exp(-z))
W1 = [[-4.18501964 5.33203231]
[-7.53803638 1.20755888]
[-4.19301361 5.32615356]
[ 7.53798951 -1.2075854 ]]
b1 = [[ 2.32933188]
[ 3.81002159]
[ 2.33009153]
[-3.8101016 ]]
W2 = [[-6033.82354742 -6008.14298684 -6033.08777738 6008.07944581]]
b2 = [[-52.67924992]]
4.8 预测¶
① 构建predict()来使用模型进行预测。
② 使用正向传播来预测结果。
note:\(y\_{prediction} = \mathbb 1 \text{{activation > 0.5}} = \begin{cases} 1 & \text{if}\ activation > 0.5 \\ 0 & \text{otherwise} \end{cases}\)
note:如果你想基于阈值将矩阵X设为0和1,则可以执行以下操作: X_new = (X > threshold)
In [151]:
def predict(parameters, X):
"""
使用学习的参数,为X中的每个示例预测一个类
参数:
parameters - 包含参数的字典类型的变量。
X - 输入数据(n_x,m)
返回
predictions - 我们模型预测的向量(红色:0 /蓝色:1)
"""
# 使用前向传播计算概率,并使用 0.5 作为阈值将其分类为 0/1。
A2, cache = forward_propagation(X, parameters)
predictions = np.round(A2)
return predictions
③ 现在运行模型以查看其如何在二维数据集上运行。
④ 运行以下代码以使用含有\(n\_h\)隐藏单元的单个隐藏层测试模型。
In [152]:
# 测试一下 predict 函数
print("=========================测试predict=========================")
parameters, X_assess = predict_test_case()
predictions = predict(parameters, X_assess)
print("预测的平均值= " + str(np.mean(predictions)))
=========================测试predict=========================
预测的平均值= 0.6666666666666666
⑤ 现在我们把所有的东西基本都做完了,我们开始正式运行。
5. 正式运行¶
5.1 构建训练模型¶
In [216]:
# 用 n_h 维隐藏层构建一个模型
X, Y = load_planar_dataset()
parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)
Cost after iteration 0: 0.693048
Cost after iteration 1000: 0.288083
Cost after iteration 2000: 0.254385
Cost after iteration 3000: 0.233864
Cost after iteration 4000: 0.226792
Cost after iteration 5000: 0.222644
Cost after iteration 6000: 0.219731
Cost after iteration 7000: 0.217504
Cost after iteration 8000: 0.219447
Cost after iteration 9000: 0.218605
5.2 绘制决策边界¶
In [217]:
# 绘制决策边界
# Y = Y.ravel() #确保 Y为一维数组
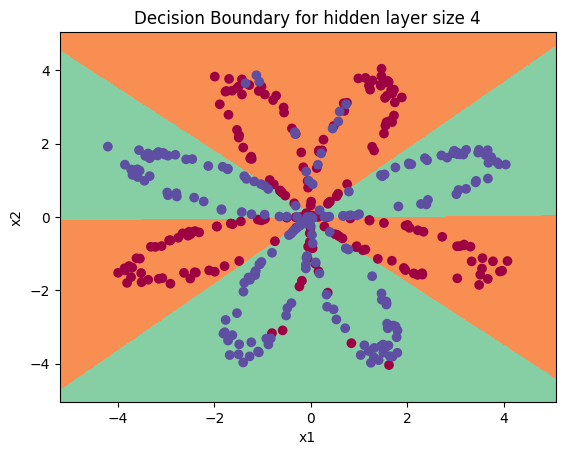
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
Out[217]:
Text(0.5, 1.0, 'Decision Boundary for hidden layer size 4')
5.3 打印准确率¶
In [221]:
# 打印准确率
predictions = predict(parameters, X)
# print ('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
accuracy = np.mean(predictions == Y) * 100 #当前版本推荐的公式
print ("准确率: {} %".format(accuracy))
准确率: 90.5 %
① 与Logistic回归相比,准确性确实更高。
② 该模型学习了flower的叶子图案!与逻辑回归不同,神经网络甚至能够学习非线性的决策边界。
5.4 调节隐藏层节点数量¶
① 现在,让我们尝试几种不同的隐藏层大小。
② 调整隐藏层大小(可选练习)运行以下代码(可能需要1-2分钟),你将观察到不同大小隐藏层的模型的不同表现。
In [222]:
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 10, 20] # 隐藏层数量
# X, Y = load_planar_dataset() #重新加入初识数据集即可解决报错问题
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(5, 2, i+1)
plt.title('Hidden Layer of size %d' % n_h)
parameters = nn_model(X, Y, n_h, num_iterations = 5000)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
predictions = predict(parameters, X)
# accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)
accuracy = np.mean(predictions == Y) * 100 #当前版本推荐的公式
print ("隐藏层的节点数量: {} ,准确率: {} %".format(n_h, accuracy))
隐藏层的节点数量: 1 ,准确率: 67.5 %
隐藏层的节点数量: 2 ,准确率: 67.25 %
隐藏层的节点数量: 3 ,准确率: 90.75 %
隐藏层的节点数量: 4 ,准确率: 90.5 %
隐藏层的节点数量: 5 ,准确率: 91.25 %
隐藏层的节点数量: 10 ,准确率: 90.25 %
隐藏层的节点数量: 20 ,准确率: 90.5 %
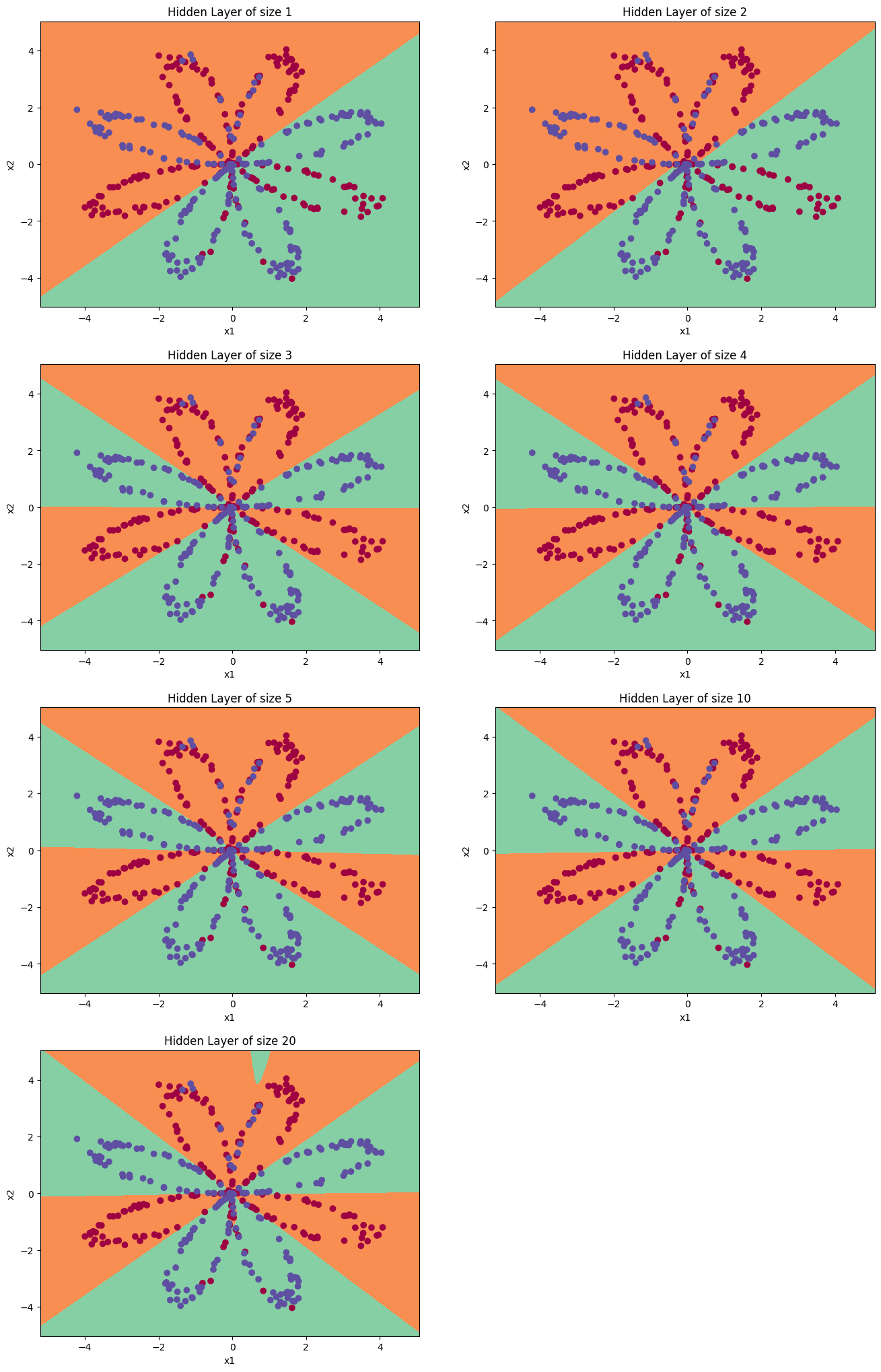
③ 较大的模型(具有更多隐藏单元)能够更好地适应训练集,直到最终的最大模型过度拟合数据。
④ 最好的隐藏层大小似乎在n_h = 5附近。实际上,这里的值似乎很适合数据,而且不会引起过度拟合。
⑤ 我们还将在后面学习有关正则化的知识,它允许我们使用非常大的模型(如n_h = 50),而不会出现太多过度拟合。

 本文主要是练习神经网络中的一些题目,从神经网络的相关模型到最后训练模型并打印结果
本文主要是练习神经网络中的一些题目,从神经网络的相关模型到最后训练模型并打印结果

 浙公网安备 33010602011771号
浙公网安备 33010602011771号