最近在开课吧学大数据课程接触到了冒泡排序和二分查找，之前虽然听说过，但是没实际接触到，现在学了一下感觉对我这种转行到Java的小白来说受益匪浅！

接下来先说说：

冒泡排序

名字由来:
　　是因为最小（或最大）的元素会经由交换慢慢“浮”到数列的顶端（降序或升序），就如同水中的气泡最终会上浮到
顶端一样，故名“冒泡排序”。

 

原理：

- 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
- 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的
数。
- 针对所有的元素重复以上的步骤，除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

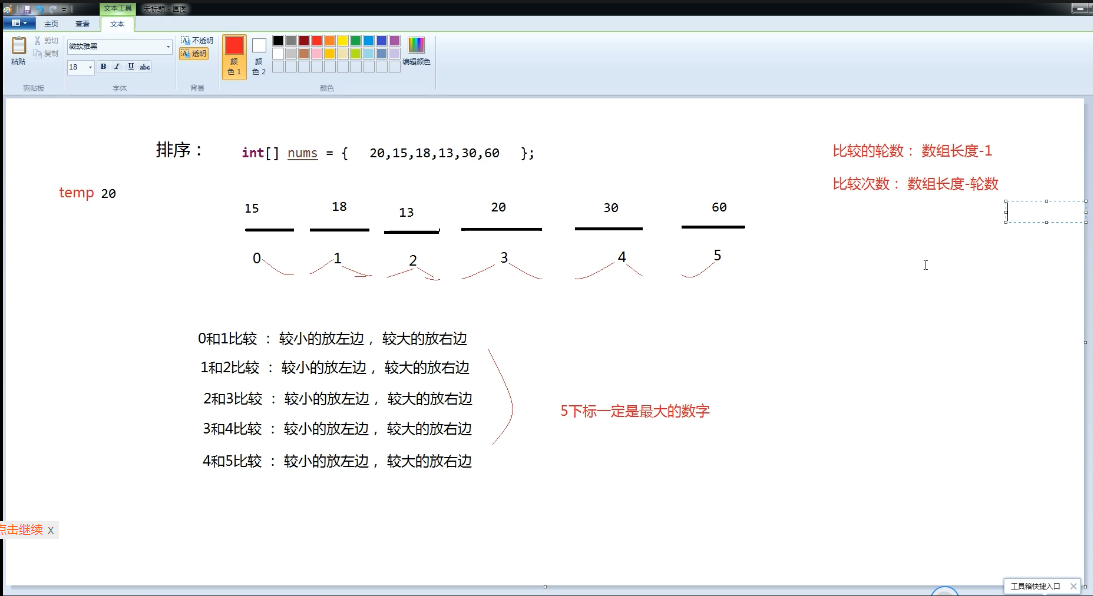
这里有两个小口诀：

升序排列的口诀:

　　N个数字来排队
　　两两相比小靠前,
　　外层 循环length-1
　　内层循环length-i-1


降序排序的口诀:


　　N个数字来排队
　　两两相比大靠前,
　　外层 循环length-1
　　内层循环length-i-1

 

二分查找（折半查找）

 

概述：

　　二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，二分查找要求数组数据必须采用顺
序存储结构有序排列。

 

原理：

　　

　　首先，假设数组中元素是按升序排列，将数组中间位置的数据与查找数据比较，如果两者相等，则查找成功；否则利用
中间位置记录将数组分成前、后两个子数组，如果中间位置数据大于查找数据，则进一步查找前子数组，否则进一步查
找后子数组。
　　重复以上过程，直到找到满足条件的数据，则表示查找成功，
直到子数组不存在为止，表示查找不成功。

　　

 

 

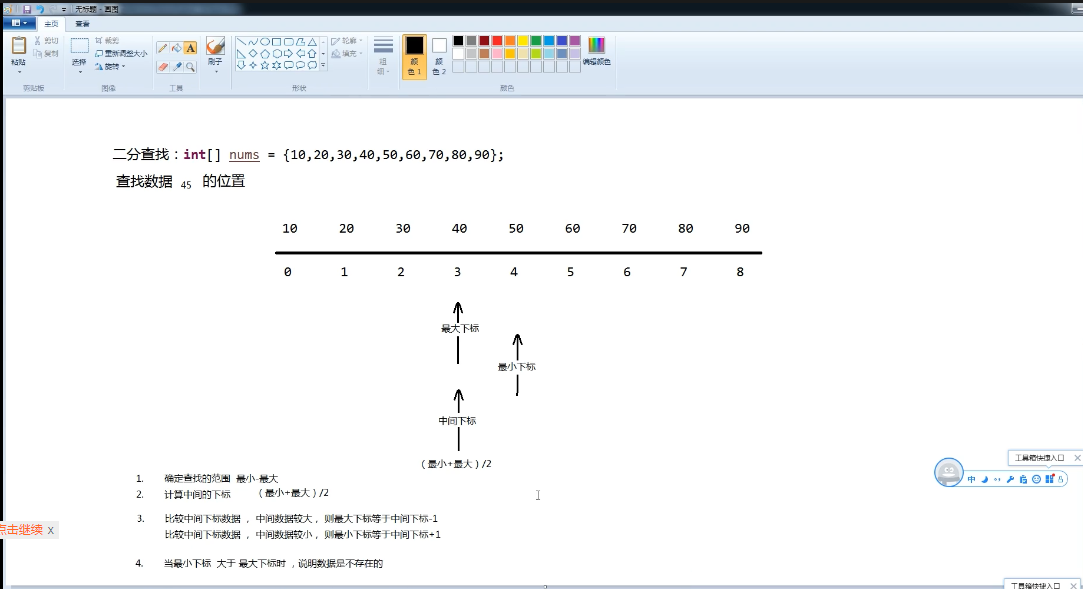
最后有个两个同时都用到的小实例：

　　

package list;

public class Demo4 {
    /**
     * 对数组{1，3，9，5，6，7，15，4，8}进行排序，然后使用二分查找 6 并
        输出排序后的下标。
     * @param args
     */
    public static void main(String[] args) {
        int[] muns = {1,3,9,5,6,7,15,4,8};
        int h;
        //使用冒泡排序
        //外层循环比较轮数
        for(int i = 0;i<muns.length-1;i++) {
            for(int j = 0;j<muns.length-i-1;j++) {
                //内层循环比较次数
                if(muns[j]>muns[j+1]) {
                    //两两相比，满足移动条件
                    h = muns[j];
                    muns[j] = muns[j+1];
                    muns[j+1] = h;
                }
            }
        };
        
        //使用二分查找方法查找
        int c = 6;
        //最小值下标
        int minIndex = 0;
        //最大值下标
        int maxIndex = muns.length-1;
        //中间数下标
        int centerIndex = (minIndex+maxIndex)/2;
        while(true) {
            if(c>muns[centerIndex]) {
                //中间数小
                minIndex = centerIndex+1;
            }else if(c<muns[centerIndex]) {
                //中间数大
                maxIndex = centerIndex-1;
            }else {
                //找到数据
                break;
            }
            
            if(minIndex>maxIndex) {
                centerIndex = -1;
                break;
            }
            //当界限发生变化，需要更新中间下标
            centerIndex = (minIndex+maxIndex)/2;
        }
        
        System.out.println("位置是："+centerIndex);
    }
}

end~