线段树优化建图

线段树优化建图

神奇数据结构QwQ

本蒟蒻学习的时候在网上找到了一堆讲解

但是都没有图片讲解 于是写下了这一篇有精美图片的随笔

1. 概念

1.1.本质

本质就是用两颗线段树优化建图（节省空间）

1.2.作用

看标题可以知道 这东西其实就是一个辅助（优化）我们建图的东西

可以辅助（优化）我们干些什么：

  1. 点向区间连边
  2. 区间向点连边
  3. 区间向区间连边

2.实现

2.1.口胡（实则不然）

（为什么要优化？）

如果我们要将图上的\([l_1,r_1]\)区间向\([l_2,r_2]\)区间中的每一个点连一条边

那么这一个小操作需要连\((r_1-l_1+1)*(r_2-l_2+1)\)条边，如果有一个\(l\),\(r\)区间很大的操作我们就寄寄了，光是存边就可能会炸掉

（用虚点行吗？）

考虑：使用虚点（就是一个我们强行加进去的一个原图上不存在的点）

把\([l_1,r_1]\)中的每一个点向虚点连一条边，然后虚点向\([l_2,r_2]\)中每一个点连一条边

os:我的图片好精美😋

这个网站太好用了 https://app.diagrams.net/

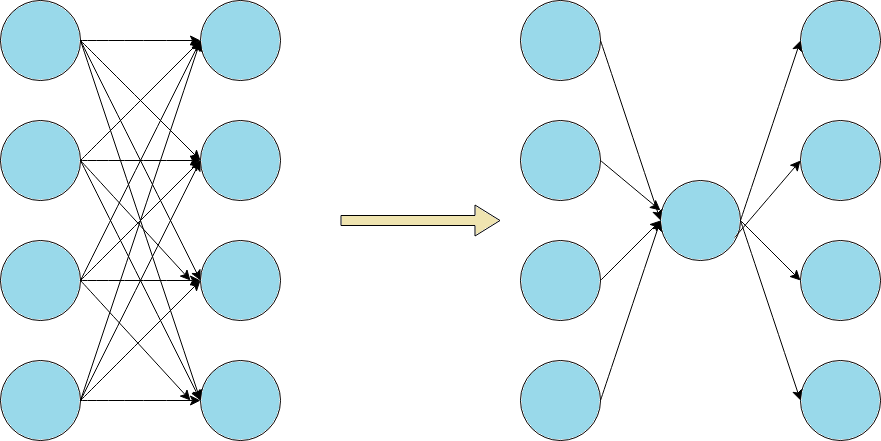
这样我们就成功地把\((r_1-l_1+1)*(r_2-l_2+1)\)条边缩减到了\((r_1-l_1+1)+(r_2-l_2+1)\)条边

但是如果有\(n\)个操作我们就又寄寄了

（怎么办？）

回归到今天的知识点

梳理一下现在的信息：我们每一次需要把一堆点连到一个点上 然后把一个点向一堆点连线

我们看第二个点像什么东西呢？ \(tree\)！！！

为了方便实现区间操作，自然地想到了线段树！

（怎么用？）

还是先看第二个问题：把一个点向一堆点连线

那么我们直接在原图基础上在旁边加一颗线段树，并把要连的点连到对应的线段树的点上

\(（1->[2,4]）\)

这样我们不管连多大的区间，最多也就只需要连\(logn\)级别的边数

第二个问题是解决了，那第一个问题呢?

第二个问题实现的是点到区间的映射，第一个问题实现的是区间到点的映射

这两个刚好反过来了，于是我们考虑把线段树倒过来：本来是父亲指向儿子，我们把它变成儿子指向父亲

这样从\([1,2]\)的一条出边（从\([1,2]\)向其他点连的边）就可以使\([1,2]\)整个区间内的点都连出去了

画一下：

这样就成功实现了！！！

为了方便表示：我们把第一个图中的树叫做出树，第二个图的叫做入树（这里就理解成父节点连的是出边还是入边就好，不然容易被绕晕）

2.2.代码实现

2.2.1.建树(build)

在建树的时候记得边权全部赋0（具体可根据题意调整）

struct Edge{
	int to,w;//id 花费 
};vector<Edge> e[N];//邻接链表

inline void add_edge(int u,int v,int w){//u->v
	e[u].push_back({v,w});
}

inline void build_out(int &o,int l,int r){//建出树
	if(l==r)return o=l,void();
    /*
    if(l==r)return o=l,void();
    相当于：
	if(l==r){
	   o=l;
	   return;
	}
    */
	o=++node_tot;
	int mid=(l+r)>>1;
	build_out(lc[o],l,mid),build_out(rc[o],mid+1,r);
	add_edge(o,lc[o],0),add_edge(o,rc[o],0);
}

inline void build_in(int &o,int l,int r){//建入树
	if(l==r)return o=l,void();
	o=++node_tot;
	int mid=(l+r)>>1;
	build_in(lc[o],l,mid),build_in(rc[o],mid+1,r);
	add_edge(lc[o],o,0),add_edge(rc[o],o,0);
}

2.2.2.连边(update)

inline void update_out(int o,int l,int r,int L,int R,int u,int w){//u->[L,R]连边 权值为w
	if(L<=l&&r<=R)return add_edge(u,o,w),void();
	int mid=(l+r)>>1;
	if(L<=mid)update_out(lc[o],l,mid,L,R,u,w);
	if(R>mid)update_out(rc[o],mid+1,r,L,R,u,w);
}

inline void update_in(int o,int l,int r,int L,int R,int u,int w){//[L,R]->u连边 取值为w
	if(L<=l&&r<=R)return add_edge(o,u,w),void();
	int mid=(l+r)>>1;
	if(L<=mid)update_in(lc[o],l,mid,L,R,u,w);
	if(R>mid)update_in(rc[o],mid+1,r,L,R,u,w);
}

3.例题

CF786B Legacy

CF，luogu

给定 \(n\) 个节点，参数 \(s\)，有 \(m\) 次操作：

  1. 给定参数 \(v,u,w\)，从 \(v\) 向 \(u\) 连一条权值为 \(w\) 的边。
  2. 给定参数 \(v,l,r,w\)，从 \(v\) 向 连 \([l,r]\) 一条权值为 \(w\) 的边。
  3. 给定参数 \(v,l,r,w\) ，从 \([l,r]\) 向 \(v\) 连一条权值为 \(w\) 的边。

求 \(s\) 到每个节点的最短路。
\(1≤n,q≤10^5,1≤w≤10^9\)
\(2s，256MB\)。

板子题 把上面的入树出树和原图的\(n\)个点放在一起建一堆边，然后跑Dijikstra即可

附上本蒟蒻的丑陋代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=4e5+10;
const int INF=0x3f3f3f3f3f3f3f3f;
int n,s,Q;
struct Edge{
	int to,w;
};vector<Edge> e[N];
bool operator<(const Edge &x,const Edge &y){
	return x.w>y.w;
}inline void add_edge(int u,int v,int w){
	e[u].push_back({v,w});
}
int lc[4*N],rc[4*N];
int node_tot;
int root_out;
int root_in;
int dis[N];
int vis[N];
priority_queue<Edge> q;
inline void build_out(int &o,int l,int r){
	if(l==r)return o=l,void();
	o=++node_tot;
	int mid=(l+r)>>1;
	build_out(lc[o],l,mid),build_out(rc[o],mid+1,r);
	add_edge(o,lc[o],0),add_edge(o,rc[o],0);
}inline void build_in(int &o,int l,int r){
	if(l==r){
		o=l;
		return;
	}
	o=++node_tot;
	int mid=(l+r)>>1;
	build_in(lc[o],l,mid);
	build_in(rc[o],mid+1,r);
	add_edge(lc[o],o,0);
	add_edge(rc[o],o,0);
}
inline void update_out(int o,int l,int r,int L,int R,int u,int w){
	if(L<=l&&r<=R)return add_edge(u,o,w),void();
	int mid=(l+r)>>1;
	if(L<=mid)update_out(lc[o],l,mid,L,R,u,w);
	if(R>mid)update_out(rc[o],mid+1,r,L,R,u,w);
}inline void update_in(int o,int l,int r,int L,int R,int u,int w){
	if(L<=l&&r<=R)return add_edge(o,u,w),void();
	int mid=(l+r)>>1;
	if(L<=mid)update_in(lc[o],l,mid,L,R,u,w);
	if(R>mid)update_in(rc[o],mid+1,r,L,R,u,w);
}
inline void Type1(){int v,u,w;cin>>v>>u>>w;add_edge(v,u,w);}
inline void Type2(){int v,l,r,w;cin>>v>>l>>r>>w;update_out(root_out,1,n,l,r,v,w);}
inline void Type3(){int v,l,r,w;cin>>v>>l>>r>>w;update_in(root_in,1,n,l,r,v,w);}
inline void dijikstra(){
	for(int i=1;i<=node_tot;i++){
		dis[i]=INF;
	}
	dis[s]=0;
	q.push({s,0});
	while(!q.empty()){
		Edge top=q.top();
		q.pop();
		int to=top.to;
		int w=top.w;
		if(vis[to])continue;
		vis[to]=true;
		for(Edge v:e[to]){
			if(dis[v.to]>dis[to]+v.w){
				dis[v.to]=dis[to]+v.w;
				q.push({v.to,dis[v.to]});
			}
		}
	}
}
inline void init(){
	cin>>n>>Q>>s;
	node_tot=n;
	build_out(root_out,1,n),build_in(root_in,1,n);
	for(int i=1;i<=Q;i++){
		int op;cin>>op;
		if(op==1)Type1();
		if(op==2)Type2();
		if(op==3)Type3();
	}
}
inline void solve(){
	dijikstra();
	for(int i=1;i<=n;i++){
		if(dis[i]==INF)cout<<-1<<" ";
		else cout<<dis[i]<<" ";
	}cout<<endl;
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	init();
	solve();
	return 0;
}

完结撒花！！！🎉🎉🎉

posted @ 2026-02-06 15:36  xwy114514  阅读(2)  评论(0)    收藏  举报