Blog大作业总结
(1)前言
1.知识点:
继承与多态的区别
1、 什么是继承,继承的特点?子类继承父类的特征和行为,使得子类具有父类的各种属性和方法。或子类从父类继承方法,使得子类具有父类相同的行为。
特点:在继承关系中,父类更通用、子类更具体。父类具有更一般的特征和行为,而子类除了具有父类的特征和行为,还具有一些自己特殊的特征和行为。
在继承关系中。父类和子类需要满足is-a的关系。子类是父类。
表示父类和子类的术语:父类和子类、超类和子类、基类和派生类,他们表示的是同一个意思。
2、 为什么需要继承?什么时候应该继承?
使用继承可以有效实现代码复用,避免重复代码的出现。
当两个类具有相同的特征(属性)和行为(方法)时,可以将相同的部分抽取出来放到一个类中作为父类,其它两个类继承这个父类。
继承实现了面向对象的原则:write once,only once(编写一次、且编写一次
3、 如何实现继承?
在Java语言中,用extends(扩展)关键字来表示一个类继承了另一个类。
在父类中只定义一些通用的属性和方法。
子类自动继承父类的属性和方法,子类中可以定义特定的属性和方法。或子类重新定义父类的属性、重写父类的方法可以获得与父类不同的功能。
4、 什么是方法重写?
如果在子类中定义的一个方法,其名称、返回类型及参数列表正好与父类中某个方法的名称、返回类型及参数列表相匹配,那么可以说,子类的方法重写了父类的方法。
方法重写在不同类,是实现多态的必要条件。
5、 super关键字的用法和位置,super关键字调用父类的构造方法,super关键字调用父类的方法?
在子类的构造方法中,通过super关键字调用父类的构造方法。
如果子类中重写了父类的方法,可以通过super关键字调用父类的方法。
父类:
private String name;
private String sex;
public xinxin1(String name,String sex)
{
this.name=name;
this.sex=sex;
}
public void hello(){
System.out.println(“嗨!我是”+name+”我是”+sex+”孩”);
}
子类:
public xinxin2(String name,String sex)
{
//调用父类的构造方法
super(name,sex);
}
public void hello(){
System.out.println(“我是新来的!”);
//调用父类的方法
super.hello();
}
位置注意:调用父类的构造方法的语句(super语句)必须是构造方法中的第一条语句。
因为创建对象的时候,需要先创建父类对象,再创建子类对象。
注意:创建对象时,先创建父类对象,在创建子类对象。如果没有显示调用父类的构造方法,将自动调用父类的无参构造方法。
6、 一切类的老大(祖先)Object。
所有类都直接或者间接地继承了java.lang.Object类,Object类中定义了所有的java对象都具有的相同行为,是所有类的祖先。
一个类如果没有使用extends关键字,那么这个类直接继承自Object类。
7、 什么是多态?
多态的特征是表现出多种形态,具有多种实现方式。或者多态是具有表现多种形态的能力的特征。或者同一个实现接口,使用不同的实例而执行不同的操作。
8、 为什么需要使用多态?多态的好处?
可以增强程序的可扩展性及可维护性,使代码更加简洁。
不但能减少编码的工作量,也能大大提高程序的可维护性及可扩展性。
9、 如何实现多态?
一般做法是:写一个方法,它只接收父类作为参数,编写的代码只与父类打交道。调用这个方法时,实例化不同的子类对象(new 一个对象)。
更具体的说:
(1)、子类重写父类的方法。使子类具有不同的方法实现。
(2)、把父类类型作为参数类型,该父类及其子类对象作为参数转入。
(3)、运行时,根据实际创建的对象类型动态决定使用那个方法。
在运行时,java虚拟机会根据实际创建的对象类型决定使用那个方法。一般将这称为动态绑定。
10、多态小结:多态与继承、方法重写密切相关,我们在方法中接收父类类型作为参数,在方法实现中调用父类类型的各种方法。当把子类作为参数传递给这个方法时,java虚拟机会根据实际创建的对象类型,调用子类中相应的方法(存在方法重写时)。
ArrList列表
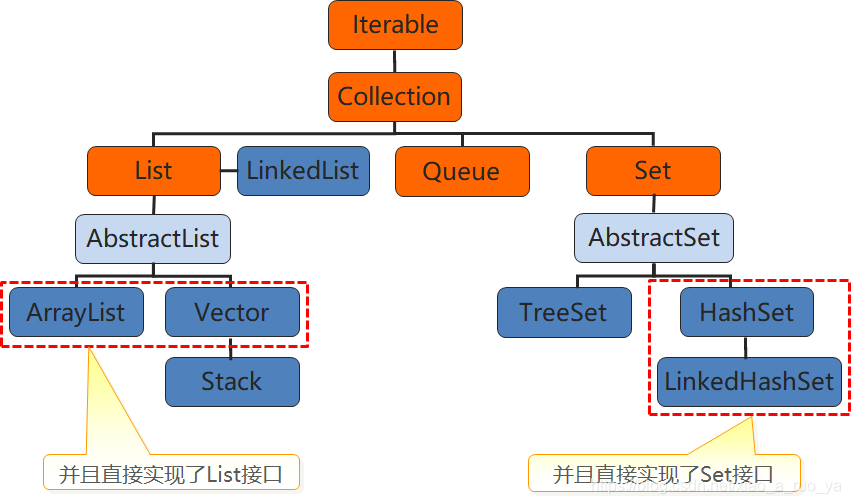
List接口常用方法:
1、add(Object element): 向列表的尾部添加指定的元素。
2、size(): 返回列表中的元素个数。
3、get(int index): 返回列表中指定位置的元素,index从0开始。
4、add(int index, Object element): 在列表的指定位置插入指定元素。
5、set(int i, Object element): 将索引i位置元素替换为元素element并返回被替换的元素。
6、clear(): 从列表中移除所有元素。
7、isEmpty(): 判断列表是否包含元素,不包含元素则返回 true,否则返回false。
8、contains(Object o): 如果列表包含指定的元素,则返回 true。
9、remove(int index): 移除列表中指定位置的元素,并返回被删元素。
10、remove(Object o): 移除集合中第一次出现的指定元素,移除成功返回true,否则返回false。
11、iterator(): 返回按适当顺序在列表的元素上进行迭代的迭代器
抽象类
那么什么叫抽象方法呢?在所有的普通方法上面都会有一个“{}”,这个表示方法体,有方法体的方法一定可以被对象直接使用。而抽象方法,是指没有方法体的方法,同时抽象方法还必须使用关键字abstract做修饰。
而拥有抽象方法的类就是抽象类,抽象类要使用abstract关键字声明。
抽象类的使用原则如下:
(1)抽象方法必须为public或者protected(因为如果为private,则不能被子类继承,子类便无法实现该方法),缺省情况下默认为public;
(2)抽象类不能直接实例化,需要依靠子类采用向上转型的方式处理;
(3)抽象类必须有子类,使用extends继承,一个子类只能继承一个抽象类;
(4)子类(如果不是抽象类)则必须覆写抽象类之中的全部抽象方法(如果子类没有实现父类的抽象方法,则必须将子类也定义为为abstract类。);
范例:
abstract class A{//定义一个抽象类
public void fun(){//普通方法
System.out.println("存在方法体的方法");
}
public abstract void print();//抽象方法,没有方法体,有abstract关键字做修饰
}
//单继承
class B extends A{//B类是抽象类的子类,是一个普通类
@Override
public void print() {//强制要求覆写
System.out.println("Hello World !");
}
}
public class TestDemo {
public static void main(String[] args) {
A a = new B();//向上转型
a.print();//被子类所覆写的过的方法
}
}
现在就可以清楚的发现:
(1)抽象类继承子类里面有明确的方法覆写要求,而普通类可以有选择性的来决定是否需要覆写;
(2)抽象类实际上就比普通类多了一些抽象方法而已,其他组成部分和普通类完全一样;
(3)普通类对象可以直接实例化,但抽象类的对象必须经过向上转型之后才可以得到。
虽然一个类的子类可以去继承任意的一个普通类,可是从开发的实际要求来讲,普通类尽量不要去继承另外一个普通类,而是去继承抽象类。
接口
接口(interface)
有时必须从几个类中派生出一个子类,继承它们所有的属性和方法。但是,Java不支持多重继承。有了接口,就可以得到多重继承的效果。
接口(interface)是抽象方法和常量值的定义的集合。
从本质上讲,接口是一种特殊的抽象类,这种抽象类中只包含常量和方法的定义,而没有变量和方法的实现。
接口定义举例
public interface Runner
int id = 1
public void start()
public void run()
public void stop()
}
案例:
蝙蝠会飞,又会用牙齿咬
首先定义一个飞行的接口:
/*
如果一个类中,既有抽象方法,又有非抽象方法,那么该类只能定义为抽象类,不能定义为接口
如果一个类中,只有抽象方法,没有非抽象方法,那么该类可以定义为接口
一般就定义为接口
定义一个接口,使用interface关键字 接口,类,枚举,注解等都是java中的类型
接口中所有的方法,都是抽象方法
所以也可以说,接口就是一个特殊的抽象类
接口中除了定义方法外,还可以定义成员变量
特点;方法和属性默认都是public修饰,也可以使用protected,但不能用private
所有的属性都是静态的常量,默认省略了static和final修饰符,属性的值必须实例化(初始化)
*/
public interface Flyable {
public final int wingsNumber = 2;
public abstract void fly();
}
接着定义一个咬人的接口:
package cn.com.Classwork190124;
public interface Bitable {
public int teethNumber = 0;
public abstract void bite();
}
最后定义蝙蝠类去实现这两个接口:
/*
在JAVA中,一个类无法继承自多个类,但是可以实现多个接口,使用关键字implements
多个接口之间使用“,”隔开 多个接口之间,没有先后顺序
这个类叫做实现类,这个类必须实现所有接口的所有方法
*/
public class Bat implements Flyable,Bitable {
@Override
public void bite() {
System.out.println("吸血");
}
@Override
public void fly() {
System.out.println("用翅膀飞");
}
public static void main(String[] args) {
System.out.println(Flyable.wingsNumber);
}
}
接口的特点:
用 interface 来定义。
接口中的所有成员变量都默认是由public static final修饰的。
接口中的所有方法都默认是由public abstract修饰的。
接口没有构造方法。构造方法用于创建对象
实现接口的类中必须提供接口中所有方法的具体实现内容。
多个无关的类可以实现同一个接口
一个类可以实现多个无关的接口
与继承关系类似,接口与实现类之间存在多态性
接口也可以继承另一个接口,使用extends关键字。
实现接口的类中必须提供接口中所有方法的具体实现内容。
多个无关的类可以实现同一个接口
一个类可以实现多个无关的接口
与继承关系类似,接口与实现类之间存在多态性
定义Java类的语法格式:
< modifier> class < name> [extends < superclass>]
[implements < interface> [,< interface>]* ] {
< declarations>*
}
此外,接口还常常被用来当做定义常量的集合:
接口也经常用来被定义常量的集合 默认省略public static final
定义更简单,使用更方便
*/
public interface Power {
int vol = 220;
double hz = 50.0;
}
- 难度:(1)第四次大作业一三题较为简单,只需简单的类和方法就可实现,而第二题关于四边形的设计则颇有难度,特别是关于第四个选项:输入六个点坐标,前两个点构成一条直线,后四个点构成一个四边形或三角形,输出直线与四边形(也可能是三角形)相交的交点数量。如果交点有两个,再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积(不换行)。若直线与四边形或三角形的一条边线重合,输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入,输出"not a quadrilateral or triangle"。对于算法知识缺乏的我,很难实现。
(2)期中考试的题目较为简单,就是基本的类的设计,继承和多态,只是我对格式输出的控制有错误。
(3)第五次大作业关于五边形的设计是我最头疼的,因为第四次大作业本就完成得不够理想,很多算法功能没有实现,因此没有前面基础的铺垫,导致我写得很吃力,有一丝茫然,感到无从下手。
(2)代码分析
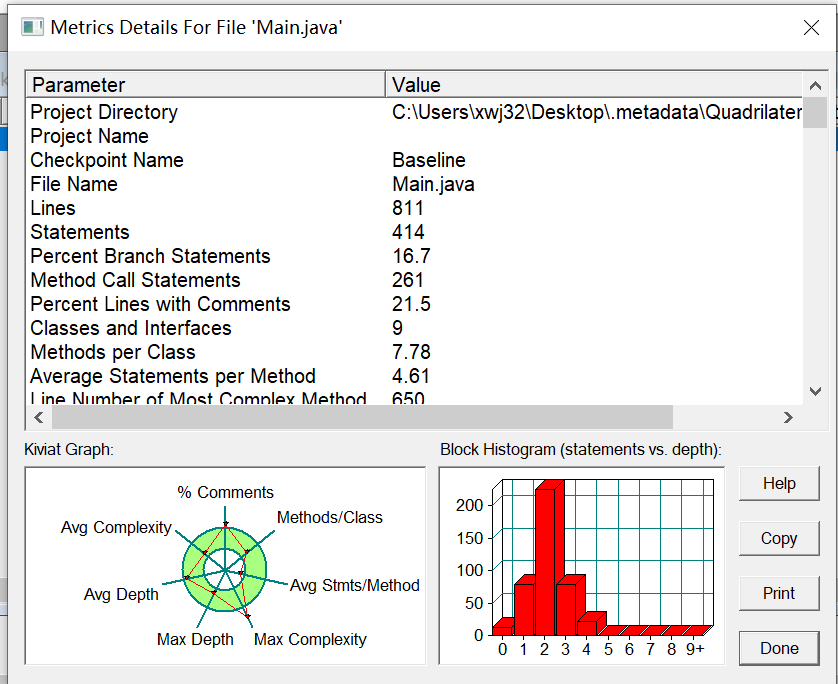
1.第四次大作业关于四边形的设计
源码:
import java.text.DecimalFormat;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s = sc.nextLine();
InputData d = new InputData();
ParseInput.paseInput(s, d);
int choice = d.getChoice();
ArrayList ps = d.getPoints();
switch (choice) {
case 1:
handle1(ps);
break;
case 2:
handle2(ps);
break;
case 3:
handle3(ps);
break;
case 4:
handle4(ps);
break;
case 5:
handle5(ps);
break;
}
}
// 输入四个点坐标,判断是否是等腰三角形、等边三角形,判断结果为true/false,两个结果之间以一个英文空格符分隔。
public static void handle1(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 4);
Quadrangle t = new Quadrangle(ps.get(0), ps.get(1), ps.get(2),ps.get(3));
t.pointsCoincideError();
System.out.println(t.Quadrangle() + " " + t.parallelogram());
}
/*输入四个点坐标,判断是否是菱形、矩形、正方形,判断结果输出true/false,
*结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
*/
public static void handle2(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 4);
Quadrangle t = new Quadrangle(ps.get(0), ps.get(1), ps.get(2),ps.get(3));
t.Quardanglejudge();t.pointsCoincideError();
System.out.println( t.rhombus()+ " " +t.rectangle() + " "
+ t.square());
}
/*输入四个点坐标,判断是凹四边形(false)还是凸四边形(true),
输出四边形周长、面积,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
*/
public static void handle3(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 4);
Quadrangle t = new Quadrangle(ps.get(0), ps.get(1), ps.get(2),ps.get(3));
t.Quardanglejudge();t.pointsCoincideError();
System.out.println(t.convex_quadrilateral()+ " " +OutFormat.doubleFormat(t.getPerimeter()) + " " + OutFormat.doubleFormat(t.getArea(t.getA(),t.getB(),t.getC(),t.getD())));
}
public static void handle4(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 6);
Line l = new Line(ps.get(0), ps.get(1));
LineInputError.pointsCoincideError(ps.get(0),ps.get(1));
if(ps.get(0).equals(ps.get(1)))
{
System.out.println("points coincide");
System.exit(0);
}
Quadrangle t = new Quadrangle(ps.get(2), ps.get(3), ps.get(4),ps.get(5));
if (t.judgeLineCoincide(l)) {
System.out.println("The line is coincide with one of the lines");
System.exit(0);
}
if(t.Quadrangle() == false){
System.out.println("not a quadrilateral or triangle");
return;
}
ps = t.getIntersections(l);
int num = ps.size();
if (num == 2) {
return;
// double[] ds = t.calArea(ps.get(0), ps.get(1));
// Arrays.sort(ds);
// System.out.println(num + " " + OutFormat.doubleFormat(ds[0]) + " " + OutFormat.doubleFormat(ds[1]));
} else {
System.out.println(num);
}
}
/*
* 输入四个点坐标,输出第一个是否在后三个点所构成的三角形的内部(输出in the triangle/outof triangle)。
* 必须使用射线法,原理:由第一个点往任一方向做一射线,射线与三角形的边的交点(不含点本身)数量如果为1,则在三角形内部。如果交点有两个或0个,则在三角形之外
* 。若点在三角形的某条边上,输出"on the triangle"
*/
public static void handle5(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 5);
Quadrangle t = new Quadrangle(ps.get(1), ps.get(2), ps.get(3),ps.get(4));
Point p = ps.get(0);
if(t.Quadrangle()){
t.pointjudge(p);
}
int i = t.isInside(p);
if(i==0) {
System.out.println("on the quadrilateral");
return;
}
if(i==-1) {
System.out.println("outof the quadrilateral");
return;
}
System.out.println("in the quadrilateral");
}
}
//用于定义一个“点”类
//判断两点是否重合
public boolean equals(Point p) {
boolean value = false;
if(this.getX() == p.getX()&&this.getY() == p.getY()){
value = true;
}
return value;
}
/* 计算当前点和输入点p之间的距离 */
public double getDistance(Point p) {
return Math.sqrt(Math.pow(this.getX()-p.getX(),2)+Math.pow(this.getY()-p.getY(),2));
}
}
class Line {
private Point p1;//线上的第一个点
private Point p2;//线上的第二个点
//构造方法
public Line(double x1, double y1, double x2, double y2) {
//在方法里new两个point对象
Point p1 = new Point(x1, y1);
Point p2 = new Point(x2, y2);
LineInputError.pointsCoincideError(p1, p2);//判断两点是否重合,重合则报错并退出
this.p1 = p1;
this.p2 = p2;
}
//一个新的构造器,参数是两个点对象
public Line(Point p1, Point p2) {
LineInputError.pointsCoincideError(p1, p2);//判断两点是否重合,重合则报错并退出
this.p1 = p1;
this.p2 = p2;
}
/* 获取线条的斜率 */
public Double getSlope() {
return (p2.getY() - p1.getY())/(p2.getX() - p1.getY());//p1,p2分别为线段的两个点
//当(x1-x2=0)注意考虑斜率不存在即返回double类型无穷大"Infinite"
}
/* 判断点x是否在线上 */
public boolean isOnline(Point x) {
// 点重合的情况
if((x.getX() == p1.getX()&&x.getY() == p1.getY())||(x.getX() == p2.getX()&&x.getY() == p2.getY())) {
return true;
}
Line l = new Line(p1, x);
//如果三个点组成的任意两条直线斜率为无穷大,则点x在线上
if (l.getSlope().isInfinite()&&this.getSlope().isInfinite()){
return true;
}
/*
* if (l.getSlope().isInfinite() || this.getSlope().isInfinite()) { return
* false; }
*/
// 此点与线上任意一点构成的线的斜率相等则此点在线上
double slope1 = l.getSlope(), slope2 = this.getSlope();
//return Math.abs(slope1 - slope2) < 0.00000000001;
return slope1 == slope2;
}
/* 获取点x到线的距离(最短距离,即垂线) */
public double getDistance(Point x) {
// 利用两点求直线方程,利用公式代入即可
// 直线方程x(y2-y1)-y(x2-x1)-x1(y2-y1)+y1(x2-x1)=0
double distY = p2.getY() - p1.getY();
double distX = p2.getX() - p1.getX();
return Math.abs(x.getX() * distY - x.getY() * distX - p1.getX() * distY + p1.getY() * distX)
/ p1.getDistance(p2);
}
/* 判断x是否在线上且在两点之间 */
public boolean isBetween(Point x) {
//System.out.println("isBetween" + " " + this.p1.x + " " + p1.y + " " + p2.x + " " + p2.y + " " + x.x + " " + x.y);
if (!this.isOnline(x)) {
return false;
}
// 与端点重合,认为不在在两点之间,
if(x.equals(p1)||x.equals(p2)){
return false;
}
// x到 p1和p2的距离 同时小于 p1到p2的距离 说明 交点在 p1到p2的线段上
double dis = p1.getDistance(p2);
boolean value = x.getDistance(p1) < dis && x.getDistance(p2) < dis;
return value;
}
/* 判断p1、p2是否在x的同一侧 */
public boolean isSameSide(Point x) {
// 点在线上且不在点之间
return isOnline(x) && !isBetween(x);
}
/* 获取p1、p2之间的中点 */
public Point getMiddlePoint() {
Point p = new Point(); //new一个新点作为p1,p2的新点
p.setX((p1.getX()+p2.getX())/2);
p.setY((p1.getY()+p2.getY())/2);
return p;
}
/* 获取线段的第一个坐标点 */
public Point getPointA() {
return p1;
}
/* 获取线段的第二个坐标点 */
public Point getPointB() {
return p2;
}
// 是否平行,平行返回true,否则false。
public boolean isParallel(Line l) {
Double b1 = this.getSlope();
Double b2 = l.getSlope();
if ((b1.isInfinite()) && (b2.isInfinite())) {
return true;
} else {
return (this.getSlope().doubleValue() == l.getSlope().doubleValue());
}
}
/* 两条线是否重合,重合返回true,否则false。*/
public boolean isCoincide(Line l) {
//先判断两条线端是否平行
if (!this.isParallel(l)) {
return false;
}
//若为平行线段,如果有一点在另一条直线上,则两条直线重合
if (this.isOnline(l.p1)) {
return true;
}
return false;
}
// 获取交叉点,若两条线平行,返回null。
public Point getIntersection(Line l) {
// LineInputError.isParallelError(this, l);
if (this.isParallel(l)) {
return null;
}
if (p1.equals(l.p1) || p1.equals(l.p2)) {
return p1;
}
if (p2.equals(l.p1) || p2.equals(l.p2)) {
return p2;
}
Point p3 = l.p1, p4 = l.p2;
double x_member, x_denominator, y_member, y_denominator;
Point cross_point = new Point();
x_denominator = p4.x * p2.y - p4.x * p1.y - p3.x * p2.y + p3.x * p1.y - p2.x * p4.y + p2.x * p3.y + p1.x * p4.y
- p1.x * p3.y;
x_member = p3.y * p4.x * p2.x - p4.y * p3.x * p2.x - p3.y * p4.x * p1.x + p4.y * p3.x * p1.x
- p1.y * p2.x * p4.x + p2.y * p1.x * p4.x + p1.y * p2.x * p3.x - p2.y * p1.x * p3.x;
if (x_denominator == 0)
cross_point.x = 0;
else
cross_point.x = x_member / x_denominator;
y_denominator = p4.y * p2.x - p4.y * p1.x - p3.y * p2.x + p1.x * p3.y - p2.y * p4.x + p2.y * p3.x + p1.y * p4.x
- p1.y * p3.x;
y_member = -p3.y * p4.x * p2.y + p4.y * p3.x * p2.y + p3.y * p4.x * p1.y - p4.y * p3.x * p1.y
+ p1.y * p2.x * p4.y - p1.y * p2.x * p3.y - p2.y * p1.x * p4.y + p2.y * p1.x * p3.y;
if (y_denominator == 0)
cross_point.y = 0;
else
cross_point.y = y_member / y_denominator;
// System.out.println(cross_point.x + ","+cross_point.y);
return cross_point; // 平行返回(0,0)
}
}
class PointInputError {
//判断从字符串中解析出的点的数量是否合格。
//静态方法
public static void wrongNumberOfPoints(ArrayList ps, int num) {
if (ps.size() != num) {
System.out.println("wrong number of points");
System.exit(0);
}
}
//判断输入的字符串中点的坐标部分格式是否合格。若不符合,报错并退出程序,静态方法
public static void wrongPointFormat(String s) {
if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) {
System.out.println("Wrong Format");
System.exit(0);
}
}
// 输入字符串是否是"选项:字符串"格式,选项部分是否是1~5其中之一,静态方法
public static void wrongChoice(String s) {
if (!s.matches("[1-5]:.+")) {
System.out.println("Wrong Format");
System.exit(0);
}
}
}
//用于格式化存储用户输入的数据,将坐标信息存入集合列表。
class InputData {
private int choice;;//用户输入的选择项
private ArrayList<Point> points = new ArrayList();//<>中为引用数据类型Point
public int getChoice() {
return choice;
}
public void setChoice(int choice) {
this.choice = choice;
}
public ArrayList<Point> getPoints() {
return points;
}
public void addPoint(Point p) { //增添点
this.points.add(p);
}
}
class ParseInput {
/*
* 输入:完整的输入字符串,包含选项和所有点的信息,格式:选项:x1,y1 x2,y2 .....xn,yn。选项只能是1-5
* 一个空InputData对象
* 处理:将输入字符串中的选项和点信息提取出来并存储到InputData对象中
* 输出:包含选项值和所有点的Point对象的InputData对象
*/
public static void paseInput(String s, InputData d) {
PointInputError.wrongChoice(s);
d.setChoice(getChoice(s));
s = s.substring(2); //截取字符串,表示索引2开始截取到整个字符串结束
pasePoints(s, d);
}
//获取输入字符串(格式:“选项:点坐标”)中选项部分
public static int getChoice(String s) {
char c = s.charAt(0);
return c - 48;
}
/*
* 输入:一个字符串,包含所有点的信息,格式:x1,y1 x2,y2 .....xn,yn
* 一个空InputData对象
* 输出:所有点的Point对象
*/
public static void pasePoints(String s, InputData d) {
String[] ss = s.split(" ");
if(ss.length == 0){
return;
}
for(int i = 0;i<ss.length;i++){
d.addPoint(readPoint(ss[i]));
}
}
/*
* 输入:包含单个点信息的字符串,格式:x,y
* 输出:Point对象
*/
public static Point readPoint(String s) {
PointInputError.wrongPointFormat(s);
String[] ss = s.split(",");
double x = Double.parseDouble(ss[0]);
double y = Double.parseDouble(ss[1]);
return new Point(x,y);
}
}
class OutFormat {
//按要求格式化实数的输出,静态方法,直接用类调用
public static Double doubleFormat(double b) {
DecimalFormat df = new DecimalFormat("###.###");
Double output = Double.valueOf(df.format(b));
return output;
}
}
class LineInputError {
// 直线的两点重合的错误判断和提示。
public static void pointsCoincideError(Point p1, Point p2) {
if ((p1.getX() == p2.getX()) && p1.getY() == p2.getY()) {
System.out.println("points coincide");
System.exit(0);
}
}
}
class Quadrangle {
private Point A;
private Point B;
private Point C;
private Point D;
public Quadrangle(Point A, Point B, Point C,Point D) {
this.A = A;
this.B = B;
this.C = C;
this.D = D;
// if (!this.isTriangle()) {
// System.out.println("data error");
// System.exit(0);
// }
}
/* 判断四个点的坐标是否能构成一个四边形 */
public boolean Quadrangle(){
if(this.pointsCoincideError1()){
return false;
}
Line l1 = new Line(B,C);
Line l2 = new Line(B,D);
Line l3 = new Line(C,D);
return !l1.isOnline(A) || !l2.isOnline(A) || !l3.isOnline(B) || !l3.isOnline(A);
}
public void Quardanglejudge(){
if(!Quadrangle())
{
System.out.println("not a quadrilateral");
System.exit(0);
}
}
//判断四个点能否构成平行四边形
public boolean parallelogram(){
boolean value = false;
if(this.Quadrangle() == false){
return false;
}
Line l1 = new Line(A,B);
Line l2 = new Line(D,C);
if(l1.getSlope() == l2.getSlope()&& A.getDistance(B) == D.getDistance(C)){
value = true;
}
return value;
}
//判断四个点能否构成菱形
public boolean rhombus() {
boolean value = false;
if (Quadrangle() && parallelogram()) {
if (A.getDistance(B) == B.getDistance(C)) {
value = true;
return value;
}
}
return value;
}
/*判断四个点能否构成矩形*/
public boolean rectangle(){
boolean value = false;
if (Quadrangle() && parallelogram()) {
if(A.getDistance(C) == B.getDistance(D)){
value = true;
return value;
}
}
return value;
}
/*判断四个点能否组成正方形*/
public boolean square(){
boolean value = false;
if(rectangle()){
if(A.getDistance(D) == A.getDistance(B)){
value = true;
return value;
}
}
return value;
}
/*判断四个点组成的四边形是凸四边形*/
public boolean convex_quadrilateral(){
boolean value = false;
if(Quadrangle() == false){
System.out.println("not a quadrilateral");
System.exit(0);
}else{
double S1 = getArea(A,B,C) + getArea(A,C,D);
double S2 = getArea(A,B,D) + getArea(B,C,D);
if(S1 == S2){
value = true;
return value;
}
}
return value;
}
/*判断四个点是否有重合点*/
public void pointsCoincideError(){
if( A.equals(B) || A.equals(C) || A.equals(D) || B.equals(C) || B.equals(D) || C.equals(D)){
System.out.println("points coincide");
System.exit(0);
}
return;
}
public boolean pointsCoincideError1() {
if( A.equals(B) || A.equals(C) || A.equals(D) || B.equals(C) || B.equals(D) || C.equals(D)){
return true;
}
return false;
}
// /* 获取三角形的中点(三条中线的交点) */
// public Point getMidpoint() {
// // 中点即重心,利用性质求解
// Point p = new Point();
// p.setX((this.x.getX() + this.y.getX() + this.z.getX()) / 3);
// p.setY((this.x.getY() + this.y.getY() + this.z.getY()) / 3);
// return p;
// }
//
// /* 获取三角形的三条边线 */
// public Line[] getSideline() {
// // 设置第一条边线
// Line line1 = new Line(x, y);
//
// // 设置第二条中线
// Line line2 = new Line(x, z);
// // 设置第三条中线
// Line line3 = new Line(y, z);
//
// Line[] lines = { line1, line2, line3 };
// return lines;
// }
/* 获取三角形的面积,此处采用海伦公式 */
public double getArea(Point A,Point B,Point C) {
double a = A.getDistance(B);
double b = A.getDistance(C);
double c = B.getDistance(C);
double p =(a+b+c)/2;
return Math.sqrt(p*(p-a)*(p-b)*(p-c));
}
/*计算四边形的面积*/
// public double getArea(Point A,Point B,Point C,Point D){
// double a = A.getDistance(B);//01
// double b = B.getDistance(C);//12
// double c = C.getDistance(D);//23
// double d = D.getDistance(B);//31
// double e = D.getDistance(A);//13
// double s = (a+b+e)/2.0;
// double s1 = (c + d + e)/2.0;
// double area1 = Math.sqrt(s*(s-a)*(s-b)*(s-e));
// double area2 = Math.sqrt(s1*(s1-c)*(s1-d)*(s1-e));
// return area1 + area2;
// }
public double getArea(Point A,Point B,Point C,Point D){
double s1 = getArea(A,C,D);
double s2 = getArea(A,B,D);
double S = s1 + s2;
return S;
}
/* 获取四边形的周长 */
public double getPerimeter() {
return A.getDistance(B) + A.getDistance(D) + B.getDistance(C)+C.getDistance(D);
}
//判断点p是否为四边形的顶点
public boolean isVertex(Point p) {
return p.equals(A) || p.equals(B) || p.equals(C)||p.equals(D);
}
/*
* 判断点p是否在本三角形内部(射线法)
* 输出:1:在内部,-1:在外部,0:在三角形上
*/
public int isInside(Point p) {
//int i = 0;
if (this.isOnTheEdge(p)) {
return 0;
}
if (isVertex(p)) {
return 0;
}
Point pb;
Line l;
if (p.x == 0 && p.y == 0) {
pb = new Point(0, 1);
l = new Line(p, pb);
} else {
pb = new Point(0, 0);
l = new Line(p, pb);
}
ArrayList<Point> ps = this.getIntersections(l);//获取直线与三角形的交点列表
int num = ps.size();
if (num == 0||num==1) {
return -1;
}
if(num == 2) {
Line l1 = new Line(ps.get(0),ps.get(1));
if(l1.isBetween(p)) {
return 1;
}else {
return -1;
}
}
return 0;
}
// 获取直线l与四边形的交点,如果没有,数组为空。
public ArrayList<Point> getIntersections(Line l) {
ArrayList<Point> pointList = new ArrayList<>();
ArrayList<Line> lines = new ArrayList<>();
int k = 0;
Line AB = new Line(A,B);
Line BC = new Line(B,C);
Line CD = new Line(C,D);
Line DA = new Line(D,A);
lines.add(0,AB);
lines.add(1,BC);
lines.add(2,CD);
lines.add(3,DA);
for(int i =0;i<lines.size();i++){
if(l.getIntersection(lines.get(i)) != null){
pointList.add(l.getIntersection(lines.get(i)));
}
}
return pointList;
}
/*
* 计算三角形上两个点所切分出的两个区域的面积。
* 输入:在三角形三条边上的两个点,要求都不为null,且不在同一条边。
* 输入为null将会导致异常。
* 输出:两部分的面积,并按小-大的顺序排序。
*/
// public double[] calArea(Point p1, Point p2) {
//
//
/* 计算三角形和本三角形的面积差
* 输入:一个三角形 ,输入约束:输入的三角形是本三角形切割下来的一个部分
* 计算:本三角形面积减去输入的三角形面积
* 输出:三角形相减后剩余部分的面积
*/
// public double calAreaDiffrence(Triangle t1) {
// double area = t1.getArea();
// area = getArea() - area;
// return area;
// }
// 判断线是否与四边形的某条边重合
public boolean judgeLineCoincide(Line l) {
boolean value = false;
Line AB = new Line(A,B);
Line BC = new Line(B,C);
Line CD = new Line(C,D);
Line DA = new Line(D,A);
if(AB.isCoincide(l) || BC.isCoincide(l) || CD.isCoincide(l) || DA.isCoincide(l)){
value = true;
return value;
}
return value;
}
public void pointjudge(Point X){
if(this.isOnTheEdge(X)){
System.out.println("on the quadrilateral");
System.exit(0);
}
if((getArea(A,C,X)+getArea(X,C,D)+getArea(X,B,D)+getArea(X,A,B)) == getArea(A,B,C,D)){
System.out.println("in the quadrilateral");
System.exit(0);
}
else
{
System.out.println("on the quadrilateral");
System.exit(0);
}
}
/*
* 输入:点p
* 输出:p是否在本四边形的四条边线(不含顶点)上。在线上输出true,否则输出false。
*/
public boolean isOnTheEdge(Point p) {
boolean value = false;
Line AB = new Line(A,B);
Line BC = new Line(B,C);
Line CD = new Line(C,D);
Line DA = new Line(D,A);
if(AB.isOnline(p) || BC.isOnline(p) || CD.isOnline(p) || DA.isOnline(p)){
value = true;
return value;
}
return value;
}
/* 四个点的getter()和setter()方法 */
public Point getA() {
return A;
}
public void setA(Point A) {
this.A = A;
}
public Point getB() {
return B;
}
public void setB(Point B) {
this.B = B;
}
public Point getC() {
return C;
}
public void setC(Point C) {
this.C = C;
}
public Point getD() {
return D;
}
public void setD(Point d) {
this.D = d;
}
}
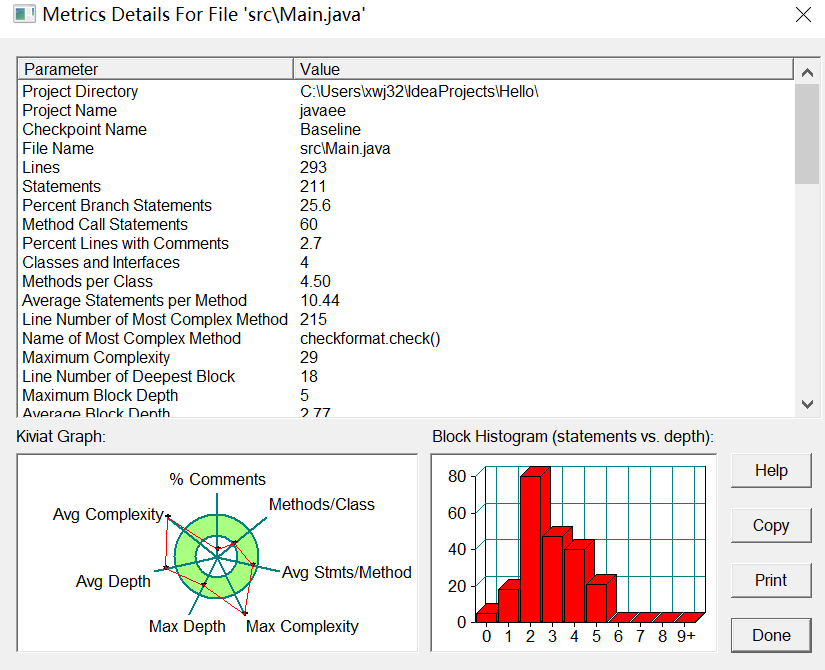
2.期中考试代码分析
源码:import java.math.BigDecimal;
import java.math.RoundingMode;
import java.util.ArrayList;
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
ArrayList<Element> s = new ArrayList<>();
int choice = sc.nextInt();
/*1:向容器中增加Point对象
2:向容器中增加Line对象
3:向容器中增加Plane对象
4:删除容器中第index - 1个数据,若index数据非法,则无视此操作
0:输入结束*/
while(choice != 0) {
switch(choice) {
case 1:Point p= new Point(sc.nextDouble(),sc.nextDouble());
s.add(p);
//insert Point object into list
break;
case 2:s.add(new Line(new Point(sc.nextDouble(),sc.nextDouble()),new Point(sc.nextDouble(),sc.nextDouble())));
//insert Line object into list
break;
case 3:s.add(new Plane(sc.next()));
//insert Plane object into list
break;
case 4:
//delete index - 1 object from list
int index = sc.nextInt();
if(s.get(index-1) != null){
s.remove(index-1);
}
}
choice = sc.nextInt();
}
for(int i =0;i<s.size();i++){
s.get(i).display();
}
}
}
class Element{
public void display(){
}
}
class Plane extends Element{
private String color;
public Plane(String color){
this.color = color;
}
public String getColor() {
return color;
}
public void setColor(String color) {
this.color = color;
}
public void display(){
System.out.println("The Plane's color is:"+this.getColor());
}
}
class Point extends Element{
private double x;
private double y;
public Point(double x,double y){
this.x = x;
this.y = y;
this.judge();
}
public void setX(double x) {
this.x = x;
}
public double getX() {
return x;
}
public void setY(double y) {
this.y = y;
}
public double getY() {
return y;
}
public void display(){
double X = this.getX();
double Y = this.getY();
System.out.println("("+OutFormat.doubleFormat(X)+","+OutFormat.doubleFormat(Y)+")");
}
public void judge(){
if(this.getX()<=0||this.getX()>200||this.getY()<=0||this.getY()>200) {
System.out.println("Wrong Format");
System.exit(0);
}
}
}
class Line extends Element{
private Point A;
private Point B;
private String color;
public Line(Point A,Point B,String color){
this.A = A;
this.B = B;
this.color = color;
}
public Line(Point A,Point B){
this.A = A;
this.B = B;
}
public Line(){
}
public Point getA() {
return A;
}
public void setA(Point a) {
A = a;
}
public Point getB() {
return B;
}
public void setB(Point b) {
B = b;
}
public void setColor(String color) {
this.color = color;
}
public String getColor() {
return color;
}
public double getDistance(){
return Math.sqrt(Math.pow(A.getX() - B.getX(),2) + Math.pow(A.getY() - B.getY(),2));
}
public void display(){
System.out.println("The line's color is:"+this.color);
System.out.println("The line's begin point's Coordinate is:"+"("+OutFormat.doubleFormat(A.getX())+","+OutFormat.doubleFormat(A.getY())+")");
System.out.println("The line's end point's Coordinate is:"+"("+OutFormat.doubleFormat(B.getX())+","+OutFormat.doubleFormat(B.getY())+")");
System.out.println("The line's length is:"+OutFormat.doubleFormat(this.getDistance()));
}
}
class OutFormat {
//按要求格式化实数的输出,静态方法,直接用类调用
public static Double doubleFormat(double data) {
BigDecimal bigDecimal = new BigDecimal(data).setScale(2, RoundingMode.HALF_UP);
double output = bigDecimal.doubleValue();
return output;
}
}
- 第五次大作业代码分析
源码:
import java.text.DecimalFormat;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s = sc.nextLine();
InputData d = new InputData();
ParseInput.paseInput(s, d);
int choice = d.getChoice();
ArrayList ps = d.getPoints();
if (choice == 4) {
choice4(ps);
} else if (choice == 5) {
choice5(ps);
} else if (choice == 6)
choice3(ps);
}
public static void choice4(ArrayList<Point> ps) {
Point a = new Point();
PointInputError.wrongNumberOfPoints(ps, 10);
Pentagon t = new Pentagon(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
if (t.pentagon_coddine(ps, 10))
System.out.println("the previous pentagon coincides with the following pentagon");
else
System.out.println("the previous quadrilateral contains the following pentagon");
}
public static void choice5(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 10);
Pentagon t = new Pentagon(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
System.out.println("4.0");
}
/*输入四个点坐标,判断是凹四边形(false)还是凸四边形(true),
输出四边形周长、面积,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"*/
public static void choice3(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 6);
Point p = ps.get(0);
Pentagon t = new Pentagon(ps.get(1), ps.get(2), ps.get(3), ps.get(4), ps.get(5));
ArrayList<Point> points_list = t.polygon();
if (points_list.size() == 5 && t.point_location(ps.get(0), points_list.size())) {
System.out.println("in the pentagon");
System.exit(0);
}
if (points_list.size() == 5 && !t.point_location(ps.get(0), points_list.size())) {
System.out.println("outof the pentagon");
System.exit(0);
}
if (points_list.size() == 3 ) {
System.out.println("in the triangle");
System.exit(0);
}
else {
System.out.println("outof the triangle");
System.exit(0);
}
if (points_list.size() == 4 ) {
System.out.println("in the quadrilateral");
System.exit(0);
}
else {
System.out.println("outof the quadrilateral");
System.exit(0);
}
}
}
class Point {
public double x;
public double y;
public Point() {
}
//构造器
public Point(double x, double y) {
this.x = x;
this.y = y;
}
/* 设置坐标x,将输入参数赋值给属性x */
public void setX(double x) {
this.x = x;
}
/* 设置坐标y,将输入参数赋值给属性y */
public void setY(double y) {
this.y = y;
}
/* 获取坐标x,返回属性x的值 */
public double getX() {
return x;
}
/* 获取坐标y,返回属性y的值 */
public double getY() {
return y;
}
//判断两点是否重合
public boolean equals(Point p) {
return this.getX() == p.getX() && this.getY() == p.getY();
}
public boolean pointsame(Point a,Point b)
{
if(a.x==b.x&&a.y==b.y)
return false;
return true;
}
/* 计算当前点和输入点p之间的距离 */
public double getDistance(Point p) {
return Math.sqrt(Math.pow(this.getX()-p.getX(),2)+Math.pow(this.getY()-p.getY(),2));
}
}
class PointInputError {
//判断从字符串中解析出的点的数量是否合格。
//静态方法
public static void wrongNumberOfPoints(ArrayList ps, int num) {
if (ps.size() != num) {
System.out.println("wrong number of points");
System.exit(0);
}
}
//判断输入的字符串中点的坐标部分格式是否合格。若不符合,报错并退出程序,静态方法
public static void wrongPointFormat(String s) {
if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) {
System.out.println("Wrong Format");
System.exit(0);
}
}
// 输入字符串是否是"选项:字符串"格式,选项部分是否是1~5其中之一,静态方法
public static void wrongChoice(String s) {
if (!s.matches("[4-6]:.+")) {
System.out.println("Wrong Format");
System.exit(0);
}
}
}
//用于格式化存储用户输入的数据,将坐标信息存入集合列表。
class InputData {
private int choice;;//用户输入的选择项
private ArrayList<Point> points = new ArrayList();//<>中为引用数据类型Point
public int getChoice() {
return choice;
}
public void setChoice(int choice) {
this.choice = choice;
}
public ArrayList<Point> getPoints() {
return points;
}
public void addPoint(Point p) { //增添点
this.points.add(p);
}
}
class ParseInput {
public static void paseInput(String s, InputData d) {
PointInputError.wrongChoice(s);
d.setChoice(getChoice(s));
s = s.substring(2); //截取字符串,表示索引2开始截取到整个字符串结束
pasePoints(s, d);
}
//获取输入字符串(格式:“选项:点坐标”)中选项部分
public static int getChoice(String s) {
char c = s.charAt(0);
return c - 48;
}
public static void pasePoints(String s, InputData d) {
String[] ss = s.split(" ");
if(ss.length == 0){
return;
}
for(int i = 0;i<ss.length;i++){
d.addPoint(readPoint(ss[i]));
}
}
/*
* 输入:包含单个点信息的字符串,格式:x,y
* 输出:Point对象
*/
public static Point readPoint(String s) {
PointInputError.wrongPointFormat(s);
String[] ss = s.split(",");
double x = Double.parseDouble(ss[0]);
double y = Double.parseDouble(ss[1]);
return new Point(x,y);
}
}
class OutFormat {
//按要求格式化实数的输出,静态方法,直接用类调用
public static Double doubleFormat(double num) {
DecimalFormat df = new DecimalFormat("#.000");
Double output = Double.valueOf(df.format(num));
return output;
}
}
class Pentagon {
private Point A;
private Point B;
private Point C;
private Point D;
private Point E;
public Pentagon(Point A, Point B, Point C,Point D,Point E) {
this.A = A;
this.B = B;
this.C = C;
this.D = D;
this.E = E;
}
/*判断能否组成三角形*/
public boolean triangle(Point A,Point B,Point C){
double AB = A.getDistance(B);
double BC = B.getDistance(C);
double AC = A.getDistance(C);
return AB + BC > AC && AB +AC >BC && BC +AC > AB;
}
/* 判断四个点的坐标是否能构成一个四边形 */
public boolean Quadrangle(){
if(this.pointsCoincideError1()){
return false;
}
Line l1 = new Line(B,C);
Line l2 = new Line(B,D);
Line l3 = new Line(C,D);
return !l1.isOnline(A) || !l2.isOnline(A) || !l3.isOnline(B) || !l3.isOnline(A);
}
/* 获取三角形的面积,此处采用海伦公式 */
public double gettriangleArea(Point A,Point B,Point C) {
double a = A.getDistance(B);
double b = A.getDistance(C);
double c = B.getDistance(C);
double p =(a+b+c)/2.0;
return Math.sqrt(p*(p-a)*(p-b)*(p-c));
}
/*判断点与另外四个点点是否重合*/
public boolean pointsCoincideError1() {
return A.equals(B) || A.equals(C) || A.equals(D) ||A.equals(E) || B.equals(C) || B.equals(D) ||B.equals(E)|| C.equals(D) || C.equals(E);
}
/* 判断五个点的坐标是否能构成一个五边形 */
public boolean pentagon() {
return !pointsCoincideError1() && !point_inline();
}
/*判断能否组成五边形,不行就退出出系统*/
public void judge_pentagon(){
if(pentagon() == false){
System.out.println("not a pentagon");
System.exit(0);
}
}
/* 获取五边形的周长 */
public double getPerimeter() {
return A.getDistance(B) + B.getDistance(C) + C.getDistance(D)+D.getDistance(E) + E.getDistance(A);
}
/*获取五边形的面积*/
public double getpentagonarea(){
return gettriangleArea(A,B,C) + gettriangleArea(A,C,D) +gettriangleArea(A,D,E);
}
/*三个坐标向量叉乘*/
public boolean multiplication_cross(Point A,Point B,Point C) {
//公式:s=(x1-x3)*(y2-y3)-(x2-x3)*(y1-y3)
//当s>0时,p1,p2,p3三个点呈逆时针
//当s<0时,p1,p2,p3三个点呈顺时针
double value = (A.getX() - C.getX()) * (B.getY() - C.getY()) - (B.getX() - C.getX()) * (A.getY() - C.getY());
if (value > 0) {
return true;
}
return false;
}
/*判断凹五边形还是凸五边形*/
public boolean Convex_pentagon(){
return multiplication_cross(A,B,C)&&multiplication_cross(B,C,D)
&&multiplication_cross(C,D,E)&&multiplication_cross(D,E,A)&&multiplication_cross(E,A,B);
}
/*选项三中第一二个点重合的情况*/
public void point_coincide(Point p1,Point p2){
if(p1.equals(p2)){
System.out.println("points coincide");
System.exit(0);
}
}
/*判断任意一个点点是否另外三条直线上*/
public boolean point_inline(){
return side_boundary().get(1).isOnline(A) &&side_boundary().get(2).isOnline(A) &&side_boundary().get(3).isOnline(A)
&&side_boundary().get(2).isOnline(B) &&side_boundary().get(3).isOnline(B) &&side_boundary().get(4).isOnline(B)
&&side_boundary().get(3).isOnline(C) &&side_boundary().get(4).isOnline(C) &&side_boundary().get(0).isOnline(C)
&&side_boundary().get(4).isOnline(D) &&side_boundary().get(0).isOnline(D) &&side_boundary().get(1).isOnline(D)
&&side_boundary().get(0).isOnline(E) &&side_boundary().get(1).isOnline(E) &&side_boundary().get(2).isOnline(E);
}
public boolean pentagon_coddine(ArrayList<Point> aa,int n)
{
int i,j;
for(i = 0,j=5;i<5;i++)
{
if(aa.get(0).pointsame(aa.get(i), aa.get(j)))
return false;
j++;
}
for(i = 0,j = 9;i<5;i++)
{
if(aa.get(0).pointsame(aa.get(i), aa.get(j)))
return false;
j--;
}
return true;
}
//判断点p是否为五边形的顶点
public boolean isVertex(Point p) {
return p.equals(A) || p.equals(B) || p.equals(C) || p.equals(D) || p.equals(E);
}
//判断点是否在五边形任意一条边上
public boolean every_line(Point p){
return side_boundary().get(0).isOnline(p) || side_boundary().get(1).isOnline(p) || side_boundary().get(2).isOnline(p)
|| side_boundary().get(3).isOnline(p) || side_boundary().get(4).isOnline(p);
}
//判断点是否在五边形边线上或与顶点重合
public void point_pentagon(Point p){
if(isVertex(p) || every_line(p)){
System.out.println("on the pentagon");
System.exit(0);
}
}
//判断五个点组成的是五边形或四边形或三角形
public ArrayList<Point> polygon() {
int count1 = 0, count2 = 0;
if (pentagon()) {
return points();
}
for (int i = 0; i < 4; i++) {
for (int j = i + 1; j <= 4; j++) {
if (points().get(i).equals(points().get(j))) {
points().remove(j);
}
}
}
for (int i = 0; i <= 4; i++) {
if (i == 0) {
if (side_boundary().get(1).isOnline(points().get(0)) || side_boundary().get(2).isOnline(points().get(0)) || side_boundary().get(3).isOnline(points().get(0))) {
points().remove(i);
}
} else if (i == 1) {
if (side_boundary().get(2).isOnline(points().get(1)) || side_boundary().get(3).isOnline(points().get(1)) || side_boundary().get(4).isOnline(points().get(1))) {
points().remove(i);
}
if (i == 2) {
if (side_boundary().get(3).isOnline(points().get(2)) || side_boundary().get(4).isOnline(points().get(2)) || side_boundary().get(1).isOnline(points().get(2))) {
points().remove(i);
}
}
if(i==3) {
if (side_boundary().get(4).isOnline(points().get(3)) || side_boundary().get(0).isOnline(points().get(3)) || side_boundary().get(1).isOnline(points().get(3))) {
points().remove(i);
}
}
if(i==4) {
if (side_boundary().get(0).isOnline(points().get(4)) || side_boundary().get(1).isOnline(points().get(4)) || side_boundary().get(2).isOnline(points().get(4))) {
points().remove(i);
}
}
}
}
return points();
}
//判断点是否在任意多边形内部
public boolean point_location(Point p,int num){
boolean flag = false;
Point p1,p2;
for(int i=0,j=num -1;i<num;j=i++)
{
p1 = points().get(i);
p2 = points().get(j);
if(new Line(p1,p2).isOnline(p) ) {
System.out.println("on the triangle");
System.exit(0);
}
else if(new Line(p1,p2).isOnline(p) && num == 4){
System.out.println("on the quadrilateral");
System.exit(0);
}
else if(new Line(p1,p2).isOnline(p) && num == 5){
System.out.println("on the pentagon");
System.exit(0);
}
if( (p1.getY() - p.getY())>0 != (p2.getY() - p.getY()>0) && (p.getX()-(p.getY()-p1.getY())*(p1.getX()-p2.getX())/
(p1.getY()-p2.getY())-p1.getX())<0 )
flag = !flag;
}
return flag;
}
// bool InPolygon(Point P)
// {
// bool flag = false;
// Point P1,P2; //多边形一条边的两个顶点
// for(int i=1,j=n;i<=n;j=i++)
// {
// P1 = polygon[i];
// P2 = polygon[j];
// if(OnSegment(P1,P2,P)) return true; //点在多边形一条边上
// if( (dcmp(P1.y-P.y)>0 != dcmp(P2.y-P.y)>0) && dcmp(P.x - (P.y-P1.y)*(P1.x-P2.x)/(P1.y-P2.y)-P1.x)<0)
// flag = !flag;
// }
// return flag;
// }
//返回五边形的五条线段
public ArrayList<Line>side_boundary(){
Line AB = new Line(A,B);
Line BC = new Line(B,C);
Line CD = new Line(C,D);
Line DE = new Line(D,E);
Line EA = new Line(E,A);
ArrayList<Line> line = new ArrayList<>();
line.add(AB);
line.add(BC);
line.add(CD);
line.add(DE);
line.add(EA);
return line;
}
//返回五边形的五个点
public ArrayList<Point> points(){
ArrayList<Point> points = new ArrayList<>();
points.add(A);
points.add(B);
points.add(C);
points.add(D);
points.add(E);
return points;
}
// 获取直线l五四边形的交点,如果没有,数组为空。
public ArrayList<Point> getIntersections(Line l) {
ArrayList<Point> pointList = new ArrayList<>();
for(int i =0;i<side_boundary().size();i++){
if(l.getIntersection(side_boundary().get(i)) != null){
pointList.add(l.getIntersection(side_boundary().get(i)));
}
}
return pointList;
}
// 判断线是否与多边形的某条边重合
public void judgeLineCoincide(Line l) {
if( l.isCoincide(side_boundary().get(0)) || l.isCoincide(side_boundary().get(1)) || l.isCoincide(side_boundary().get(2))
|| l.isCoincide(side_boundary().get(3)) || l.isCoincide(side_boundary().get(4))){
System.out.println("The line is coincide with one of the lines");
System.exit(0);
}
}
/* 四个点的getter()和setter()方法 */
public Point getA() {
return A;
}
public void setA(Point A) {
this.A = A;
}
public Point getB() {
return B;
}
public void setB(Point B) {
this.B = B;
}
public Point getC() {
return C;
}
public void setC(Point C) {
this.C = C;
}
public Point getD() {
return D;
}
public void setD(Point d) {
this.D = d;
}
public Point getE() {
return E;
}
public void setE(Point e) {
E = e;
}
}
class Line {
private Point p1;//线上的第一个点
private Point p2;//线上的第二个
//一个新的构造器,参数是两个点对象
public Line(Point p1, Point p2) {
this.p1 = p1;
this.p2 = p2;
}
/* 获取线条的斜率 */
public Double getSlope() {
return (p2.getY() - p1.getY())/(p2.getX() - p1.getY());//p1,p2分别为线段的两个点
//当(x1-x2=0)注意考虑斜率不存在即返回double类型无穷大"Infinite"
}
/* 判断点x是否在线上 */
public boolean isOnline(Point x) {
// 点重合的情况
if ((x.getX() == p1.getX() && x.getY() == p1.getY()) || (x.getX() == p2.getX() && x.getY() == p2.getY())) {
return true;
}
Line l = new Line(p1, x);
//如果三个点组成的任意两条直线斜率为无穷大,则点x在线上
if (l.getSlope().isInfinite() && this.getSlope().isInfinite()) {
return true;
}
// 此点与线上任意一点构成的线的斜率相等则此点在线上
double slope1 = l.getSlope(), slope2 = this.getSlope();
return Math.abs(slope1 - slope2) < 0.00000000001;
}
/* 判断x是否在线上且在两点之间 */
public boolean isBetween(Point x) {
if (!this.isOnline(x)) {
return false;
}
// 与端点重合,认为不在在两点之间,
if(x.equals(p1)||x.equals(p2)){
return false;
}
// x到 p1和p2的距离 同时小于 p1到p2的距离 说明 交点在 p1到p2的线段上
double dis = p1.getDistance(p2);
boolean value = x.getDistance(p1) < dis && x.getDistance(p2) < dis;
return value;
}
/* 判断p1、p2是否在x的同一侧 */
public boolean isSameSide(Point x) {
// 点在线上且不在点之间
return isOnline(x) && !isBetween(x);
}
/* 获取线段的第一个坐标点 */
public Point getPointA() {
return p1;
}
/* 获取线段的第二个坐标点 */
public Point getPointB() {
return p2;
}
// 是否平行,平行返回true,否则false。
public boolean isParallel(Line l) {
Double b1 = this.getSlope();
Double b2 = l.getSlope();
if ((b1.isInfinite()) && (b2.isInfinite())) {
return true;
} else {
return (this.getSlope().doubleValue() == l.getSlope().doubleValue());
}
}
/* 两条线是否重合,重合返回true,否则false。*/
public boolean isCoincide(Line l) {
//先判断两条线端是否平行
if (!this.isParallel(l)) {
return false;
}
//若为平行线段,如果有一点在另一条直线上,则两条直线重合
if (this.isOnline(l.p1)) {
return true;
}
return false;
}
// 获取交叉点,若两条线平行,返回null。
public Point getIntersection(Line l) {
// LineInputError.isParallelError(this, l);
if (this.isParallel(l)) {
return null;
}
if (p1.equals(l.p1) || p1.equals(l.p2)) {
return p1;
}
if (p2.equals(l.p1) || p2.equals(l.p2)) {
return p2;
}
Point p3 = l.p1, p4 = l.p2;
double x_member, x_denominator, y_member, y_denominator;
Point cross_point = new Point();
x_denominator = p4.x * p2.y - p4.x * p1.y - p3.x * p2.y + p3.x * p1.y - p2.x * p4.y + p2.x * p3.y + p1.x * p4.y
- p1.x * p3.y;
x_member = p3.y * p4.x * p2.x - p4.y * p3.x * p2.x - p3.y * p4.x * p1.x + p4.y * p3.x * p1.x
- p1.y * p2.x * p4.x + p2.y * p1.x * p4.x + p1.y * p2.x * p3.x - p2.y * p1.x * p3.x;
if (x_denominator == 0)
cross_point.x = 0;
else
cross_point.x = x_member / x_denominator;
y_denominator = p4.y * p2.x - p4.y * p1.x - p3.y * p2.x + p1.x * p3.y - p2.y * p4.x + p2.y * p3.x + p1.y * p4.x
- p1.y * p3.x;
y_member = -p3.y * p4.x * p2.y + p4.y * p3.x * p2.y + p3.y * p4.x * p1.y - p4.y * p3.x * p1.y
+ p1.y * p2.x * p4.y - p1.y * p2.x * p3.y - p2.y * p1.x * p4.y + p2.y * p1.x * p3.y;
if (y_denominator == 0)
cross_point.y = 0;
else
cross_point.y = y_member / y_denominator;
return cross_point; // 平行返回(0,0)
}
}
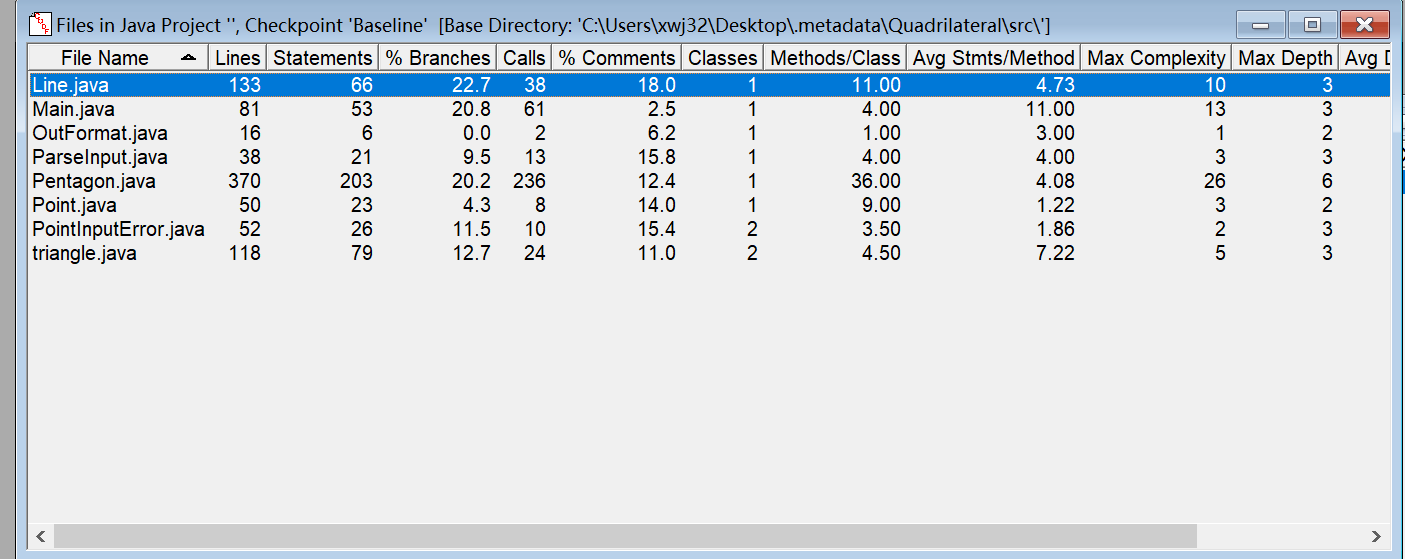
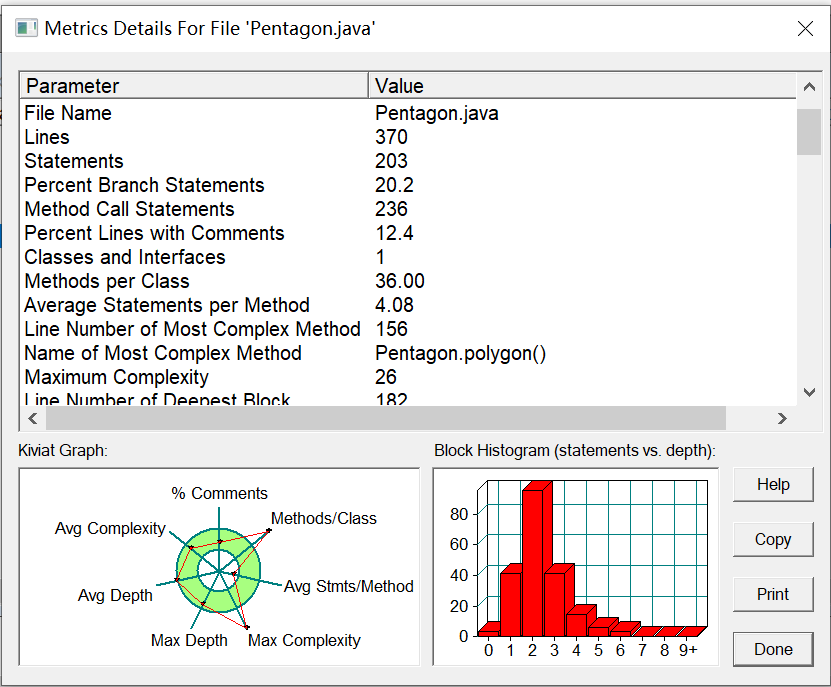

(3)踩坑心得:
1.一个类和方法只做一件事,做到低耦合,不能牵一发而动全身
2.在方法中尽量少用选择语句,如if-else,降低圈复杂度
3.在一些相似的类如果可以抽象出一些共同的属性和方法,可以适当使用继承和多态
4.要多去了解Java强大的类库
5.需要加强自己对算法的学习
6.要多练多敲代码自己的能力才会得到提升
7.使用继承和多态可以大大降低代码复杂度,提高效率
(4)改进建议
1.在以后的敲代码中,要多使用继承,,提高编码效率
2.以后要早点开始写PTA,才能做到从容不迫
3.要降低代码的耦合性,不能牵一发而动全身
4.可以去课外学习些网课,拓展知识
(5)总结
- 通过慕课的学习,了解了Java的异常机制和文件处理IO流

- 了解了throw和throws的区别
throws 与 throw 的区别
throws
用在方法声明处,其后跟着的是异常类的名字
表示此方法会抛出异常,需要由本方法的调用者来处理这些异常
但是注意:这只是一种可能性,异常不一定会发生
throw
用在方法的内部,其后跟着的是异常对象的名字
表示此处抛出异常,由方法体内的语句处理
注意:执行throw一定抛出了某种异常
- 基本了解了JavaIO流


 浙公网安备 33010602011771号
浙公网安备 33010602011771号