地铁最短路径_实现
-
主要功能
提供一副地铁线路图,输入起始站与终点站,通过地铁线路信息(data.txt),计算指定两站之间的优乘车方案(经过站点最少),输出该方案地铁线路经过的所有站点。(可显示多条最优路径)
代码及文件见此链接:https://github.com/31801156/SubwayPlanning
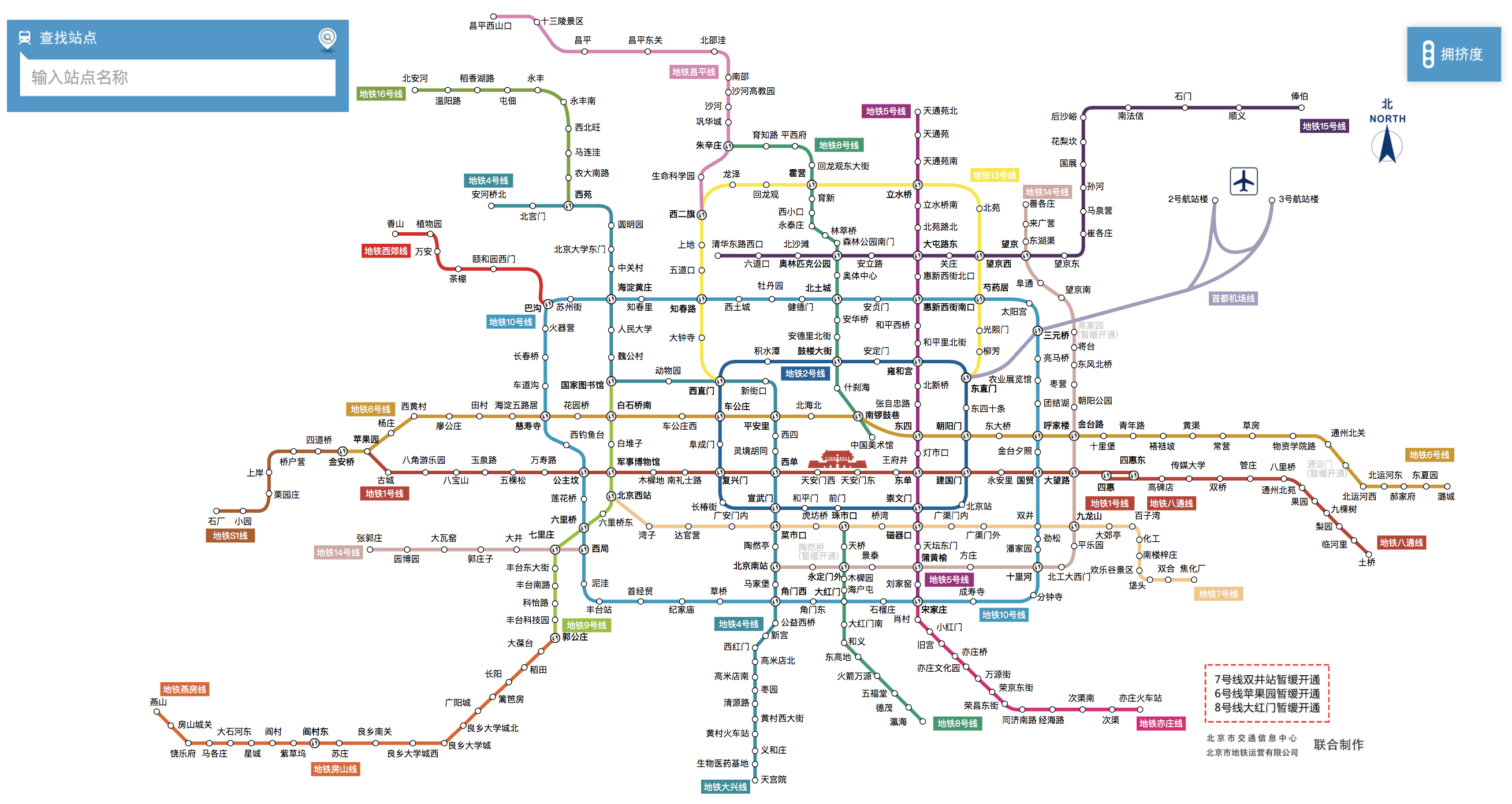
以北京地铁为例,地铁线路信息保存在data.txt中,格式如下:
地铁线路总数
线路名1 站名1 站名2 站名3 ....
线路名2 站名1 站名2 站名3 ...
线路名3 站名1 站名2 站名3 ......
- 需求分析
- 可以显示地铁线路,用户启动程序,输入操作信息,可以读取地铁线路信息;该程序能够准确地读出.txt文件中的数据。操作信息输入错误应提示。
- 实现查询操作,输入操作信息以及线路号,可以查询某条线路所经过的站点,输出该号线路上所有站点信息。
- 实现计算任意两站点间最短路径的程序Dijkstra算法,输入操作信息以及用户起始站与终点站,应能计算并输出最优的乘地铁的路线(经过的站点最少把输出结果保存到指定文件中。
没有通路应提示。
- 实现语言
java
- 实现算法
Dijkstra
- 类职责划分
1. public class Clearfile类,需要clear的文件我已经固定为result.txt文件了,File file =new File("C:\\Users\\徐梦璠0102sydxg\\Desktop\\result.txt")。程序运行开始会先进行Clearfile.Clearfile(),来清除上一次运行的结果信息。
2. public class Readfile类,获取需要读取的文件名 readfile(String filename),读取文件内容并保存。
3. public class Writefile类,将查询操作结果保存到result.txt文件,FileWriter fileWritter = new FileWriter("C:\\Users\\徐梦璠0102sydxg\\Desktop\\result.txt",true) 。
4. public class Node 类,节点类,存储各站点的信息,
public String name;
private int depth;//深度
public ArrayList<Node> parent=new ArrayList<Node>();//父亲节点
public ArrayList<Node> nearbyNode=new ArrayList<Node>();//相邻站点列表
public ArrayList<String> line=new ArrayList<String>();//所在的线路名称
public boolean flag=false;//记录状态
5. public class Line 类,线路类,存储线路信息,
public String name;
public ArrayList<String> station;//线路中的站点
6. public class Dijkstra ,Dijkstra算法为其中的一部分,该类功能主要是Dijkstra查询最短路径,设置Node类的父亲节点,在此基础上存储多条路径到
ArrayList<ArrayList<Node>> allpath=new ArrayList<ArrayList<Node>>()中。
7.public class Main 类,即主要运行类,把其它类串联起来,实现查找并输出最短路径的功能。在Main类中,涉及到 Clearfile.Clearfile() ,清空结果文件,读取键盘信息(输入以"****"结束),-map操作调用 Readfile类实现读取文件,存储站点、线路以及站点邻接关系功能并去除环线;-a操作实现查询某线路的站点信息功能;-b操作调用Dijkstra类,实现最短路径查询功能,并输出线路转换信息;-map、-a、-b查询结束,调用 Writefile类保存查询结果。
- 核心代码
- 清空result文件
public static void Clearfile() { File file =new File("C:\\Users\\徐梦璠0102sydxg\\Desktop\\result.txt"); try { if(!file.exists()) { file.createNewFile(); } FileWriter fileWriter =new FileWriter(file); fileWriter.write(""); fileWriter.flush(); fileWriter.close(); } catch (IOException e) { e.printStackTrace(); } } - 读取文件
public ArrayList<String> readfile(String filename) throws IOException{ ArrayList<String> list=new ArrayList<String>(); BufferedReader reader=null; try{ reader=new BufferedReader(new InputStreamReader(new FileInputStream(filename),"UTF-8"));//读取文件内容 String tempString=null; int line=1; //按行读取,存入list while((tempString=reader.readLine())!=null){ list.add(tempString); line++; } reader.close(); }catch(FileNotFoundException fne){ System.out.println("****************\n文件不存在,读取失败!"); System.exit(0); } finally{ if (reader!=null) { try { reader.close(); } catch (IOException e1) { } } } return list;//return } - 结果写入文件
public void writefile(String s) throws IOException { FileWriter fileWritter = new FileWriter("C:\\Users\\徐梦璠0102sydxg\\Desktop\\result.txt",true); fileWritter.write(s); fileWritter.close(); } - Dijkstra算法,函数名称虽为 public void update_nextNode(Node v) ,实际是Dijkstra算法的实现。
public void update_nextNode(Node v) { if(v==null)//站点不存在 { System.out.print("站点不存在"); System.exit(0); return; } if(v.nearbyNode.size()==0) {//没有通路了 System.out.print("查询失败!没有通路"); System.exit(0); } ArrayList<Node> nextnodeList=new ArrayList<Node>();//下一步可查询节点列表 //dijkstra最短路径 //遍历v节点的相邻节点 for(int i=0;i<v.nearbyNode.size();i++){ if(v.parent==null||!v.parent.contains(v.nearbyNode.get(i))) { Node nextnode=v.nearbyNode.get(i); //节点未查询,设置父亲节点 if(!nextnode.flag){ nextnode.setFlag(true);//记录查询状态 nextnode.setDepth(v.getDepth()+1); nextnode.parent.add(v); nextnodeList.add(nextnode); } //节点已查询,更新父亲节点 else { if(v.getDepth()+1<=nextnode.getDepth()) { nextnode.setDepth(v.getDepth()+1); if(!nextnode.parent.contains(v)) nextnode.parent.add(v); for(int k=0;k<nextnode.parent.size();k++) { if(nextnode.parent.get(k).getDepth()+1>v.getDepth()+1) { nextnode.parent.remove(k); } } nextnodeList.add(nextnode);//加入下一步可查询节点列表 } } } } //已查询到终止点,return,退出递归 if(nextnodeList.contains(v22)) { return; } //递归遍历可查询节点,更新父亲节点 for(Node n:nextnodeList) { update_nextNode(n); } } - 获取并存储多条路线
//递归获取最短路径线路信息//此递归有点深度搜索的意思,也有广度搜索的意思 public void getline(Node v2,Node v1){ if(path.contains(v1)||path.contains(v2)) { path=new ArrayList<Node>(); return; } if(v2==null||v2.parent.contains(v1)){//找到由终点--->起点的一条路径 path.add(v2); path.add(v1); allpath.add(path);//将该路径添加到allpath中 path=new ArrayList<Node>();//new path,来存储下一条路线 return;//本路径查找结束,return } for(int i=0;i<v2.parent.size();i++){//若有多条最短路径,则节点有多个父亲节点,遍历每个父亲节点,递归找寻多条路径 path.add(v2); if(v2!=null) v2=v2.parent.get(i); getline(v2,v1); } } - dijkstra(ArrayList<Node> station, String node1,String node2) ,该函数串联起 update_nextNode() 和 getline() 函数,实现最短路径查询与结果路径的处理。
public ArrayList<ArrayList<Node>> dijkstra(ArrayList<Node> station, String node1,String node2){ Node v1=new Node(); Node v2=new Node(); for(int i=0;i<station.size();i++) { if(station.get(i).name.equals(node1)){ v1=station.get(i);//出发站点类 } if(station.get(i).name.equals(node2)){ v2=station.get(i);//终止站点类 } } //查询站点不存在 if(!station.contains(v1)||!station.contains(v2)) { if(station.contains(v1)&&station.contains(v2)) { System.out.println("***********************\n输入错误!起始站点和终止站点不存在"); } else if(!station.contains(v1)) { System.out.println("***********************\n输入错误!起始站点不存在"); } else if(!station.contains(v2)) { System.out.println("***********************\n输入错误!终止站点不存在"); } System.exit(0); } setRoot(v1);//v1为根节点 //更新v1-->v2路线,查找最短路径 update_nextNode(v1); //递归获取最短路径线路信息 getline(v2,v1); // for(int i=0;i<allpath.size();i++){ // for(int j=0;j<allpath.get(i).size();j++) // System.out.print(allpath.get(i).get(j).name+" "); // System.out.println(allpath.get(i).size()); // System.out.println(); // } //查询得到的多条最短路径,需要依据前面路径补全缺失信息 if(allpath.size()>1) { for(int i=1;i<allpath.size();i++){ int c=allpath.get(i).size(); for(int j=0;j<allpath.get(i-1).size()-c;j++) allpath.get(i).add(j,allpath.get(i-1).get(j)); } } int min=100; for(int i=0;i<allpath.size();i++) { if(allpath.get(i).size()<min) { min=allpath.get(i).size(); } } for(int i=0;i<allpath.size();i++) {//去除非最短路径路线 if(allpath.get(i).size()>min) { allpath.remove(i); } } for(int i=0;i<allpath.size();i++) {//去重 for(int j=i+1;j<allpath.size();j++) if(allpath.get(i).equals(allpath.get(j))) { allpath.remove(j); } } // for(int i=0;i<allpath.size();i++) { // for(int j=0;j<allpath.get(i).size();j++) // System.out.print(allpath.get(i).get(j).name+" "); // System.out.println(allpath.get(i).size()); // System.out.println(); // } return allpath; }
- private static ArrayList trimList(ArrayList list)//去除相同元素
//使用方法trimList去除相同元素 private static ArrayList trimList(ArrayList list) { ArrayList list2 = new ArrayList(); for (int i=list.size()-1;i>=0;i--) { Object o=list.get(i); if (list2.indexOf(o)==-1) { list2.add(0,o); } } return list2; } - main()函数,串联起以上的功能,实现查询输出功能。
public static void main(String[] args) throws IOException { //清除上一次运行的结果信息 Clearfile.Clearfile(); Scanner input=new Scanner(System.in); String s1=""; String a1; for(int i=0;;i++) { a1=input.nextLine(); if(a1.equals("****"))//以一行****作为输入结束 break; String[] b1=a1.split(" "); for(int k=0;k<b1.length;k++) { s1+=b1[k]+" "; } } s1=s1.toString(); String[] input1=s1.split(" ");//保存输入信息 String file_address ="";//文件读取地址 // String write_address =""; ArrayList<Line> line=new ArrayList<Line>(); ArrayList<String> lname=new ArrayList<String>(); ArrayList<Node> station=new ArrayList<Node>(); String line0; for(int i=0;i<input1.length;i++) { //-map操作,读取文件 if("-map".equals(input1[i])){ file_address=input1[i+1]; Readfile a=new Readfile(); ArrayList<String> mapdata=a.readfile(file_address);//读取文件内容,存入mapdata //输出mapdata内容 System.out.println("***********************************************************************************"); System.out.println("-map操作查询结果如下:"); for(int j=0;j<mapdata.size();j++) { System.out.println(mapdata.get(j)); } for(int j=0;j<mapdata.size();j++) { String[] linestations=mapdata.get(j).split(" ");//线路上的站点 String linename=linestations[0];//线路名 lname.add(linename); ArrayList<String> s=new ArrayList<String>(); for(int k=1;k<linestations.length;k++) { s.add(linestations[k]); } Line line2=new Line();//Line类,存入线路信息 line2.setName(linename); line2.setStation(s); line.add(line2); for(int k=1;k<linestations.length;k++) { Node n=new Node();//站点类 n.setName(linestations[k]); int f=0; for(int p=0;p<station.size();p++){//站点存入station if(station.get(p).name==linestations[k]) { f=1; break; } } if(f==0) { station.add(n); } } } } } for (int i=0;i<input1.length; i++) { //站点邻接关系存储 if ("-map".equals(input1[i])) { file_address = input1[++i]; Readfile a=new Readfile(); ArrayList<String> map=a.readfile(file_address); for(int b=0;b<map.size();b++) { ArrayList<String> s=new ArrayList<String>(); String[] sta; sta = map.get(b).split(" "); if(sta[1].equals(sta[sta.length-1])) { sta[0]+="(环线)"; } for(int st=1;st<sta.length;st++) {//站点邻接关系存储 //站点为线路首站 if(st==0) { int nu=-1; for(int st1=0;st1<station.size();st1++) { if(station.get(st1).getName().equals(sta[st+1])) { nu=st1; } } if(nu==-1) continue; for(int st1=0;st1<station.size();st1++) { if(station.get(st1).getName().equals(sta[st])) { station.get(st1).nearbyNode.add(station.get(nu)); station.get(st1).line.add(sta[0]); } } } //站点为线路尾站 else if(st==sta.length-1) { int nu=-1; for(int st1=0;st1<station.size();st1++) { if(station.get(st1).getName().equals(sta[st-1])) { nu=st1; } } if(nu==-1) continue; for(int st1=0;st1<station.size();st1++) { if(station.get(st1).getName().equals(sta[st])) {//已有-->st1 station.get(st1).nearbyNode.add(station.get(nu)); station.get(st1).line.add(sta[0]); } } } else{ int nu1=-1; int nu2=-1; for(int st1=0;st1<station.size();st1++) { if(station.get(st1).getName().equals(sta[st-1])) { nu1=st1; } } for(int st1=0;st1<station.size();st1++) { if(station.get(st1).getName().equals(sta[st+1])) { nu2=st1; } } if(nu2==-1&&nu1==-1) continue; for(int st1=0;st1<station.size();st1++) { if(station.get(st1).getName().equals(sta[st])) { if(nu1!=-1) station.get(st1).nearbyNode.add(station.get(nu1)); if(nu2!=-1) station.get(st1).nearbyNode.add(station.get(nu2)); station.get(st1).line.add(sta[0]); } } } //去除相同元素 for(int st1=0;st1<station.size();st1++) { station.get(st1).line= trimList(station.get(st1).line); station.get(st1).nearbyNode = trimList(station.get(st1).nearbyNode); } } } // for(int st1=0;st1<station.size();st1++) { // System.out.print(station.get(st1).name+"\\"); // for(int j=0;j<station.get(st1).nearbyNode.size();j++) // System.out.print(station.get(st1).nearbyNode.get(j).name+":"); // System.out.println(); // } }} for(int i=0;i<input1.length;i++) { //-a操作,查询某条线路上的站点 if("-a".equals(input1[i])) { String linename=input1[i+1]; if(!lname.contains(linename)) { System.out.println("***********************\n输入错误!该线路不存在"); System.exit(0); } line0=linename+":"; for(int j=0;j<line.size();j++) { if(line.get(j).name.equals(linename)) { for(int k=0;k<line.get(j).station.size();k++) { line0=line0+" "+line.get(j).station.get(k); } break; } } System.out.println("***********************************************************************************"); System.out.println("※-a操作查询结果如下:"); System.out.println(line0); Writefile a=new Writefile(); a.writefile("※-a操作查询结果如下:\n"); line0+="\n"; a.writefile(line0);//查询结果写入文件 } } for(int i=0;i<input1.length;i++){ //-b操作,查询两站点间最短路径 if("-b".equals(input1[i])) { //记录起止点 if(i+2>input1.length-1) { System.out.println("*************\n信息不足,无法查询!"); System.exit(0); } start=input1[i+1]; end=input1[i+2]; if(start.equals(end)) { System.out.println("*************\n你已经到站啦!!!"); System.exit(0); } Dijkstra path_query=new Dijkstra(); ArrayList<ArrayList<Node>> a=new ArrayList<ArrayList<Node>>(); a=path_query.dijkstra(station,start,end);//dijkstra求解最短路径 String linename=null; System.out.println("***********************************************************************************"); System.out.println("※-b操作查询结果如下:"); Writefile b=new Writefile(); b.writefile("※-b操作查询结果如下:\n"); //输出线路 for(int o=0;o<a.size();o++) { String road=""; int l=o+1; System.out.println("******第"+l+"种线路******:\n"+"----共经过"+a.get(o).size()+"站----\n"); road+="******第"+l+"种线路******:\n"+"----共经过"+a.get(o).size()+"站----\n"; for(int j=a.get(o).size()-1;j>=0;j--) { //road加入换乘信息 //线路首站 if(j==a.get(o).size()-1) { for(int k=0;k<a.get(o).get(j).line.size();k++) { if(a.get(o).get(j-1).line.contains(a.get(o).get(j).line.get(k))) { linename=a.get(o).get(j).line.get(k); road+=a.get(o).get(j).line.get(k)+"\n"; System.out.println(a.get(o).get(j).line.get(k)); } } } //线路尾站,判断是否换乘 else if(j==0){ for(int k=0;k<a.get(o).get(j).line.size();k++) { if(a.get(o).get(j+1).line.contains(a.get(o).get(j).line.get(k))) {//上一站点与当前站点不在同路线上,换乘 if(!a.get(o).get(j).line.get(k).equals(linename)) { linename=a.get(o).get(j).line.get(k); System.out.println(); road+="\n"+"换乘--->"+a.get(o).get(j).line.get(k)+"\n"; System.out.println("换乘--->"+a.get(o).get(j).line.get(k)); } } } } //线路中间站,判断是否换乘 else { int f=0; for(int k=0;k<a.get(o).get(j).line.size();k++) { if(a.get(o).get(j+1).line.contains(a.get(o).get(j).line.get(k))) { if(!a.get(o).get(j).line.get(k).equals(linename)) {//上一站点与当前站点不在同路线上,换乘 linename=a.get(o).get(j).line.get(k); System.out.println(); road+="\n"+"换乘--->"+a.get(o).get(j).line.get(k)+"\n"; System.out.println("换乘--->"+a.get(o).get(j).line.get(k)); } } } } //road加入站点信息 road+=a.get(o).get(j).name+" "; System.out.print(a.get(o).get(j).name+" "); } road+="\n"; b.writefile(road);//结果写入文件 System.out.println(); } } } }
- 测试用例
1.-map操作,输出文件信息
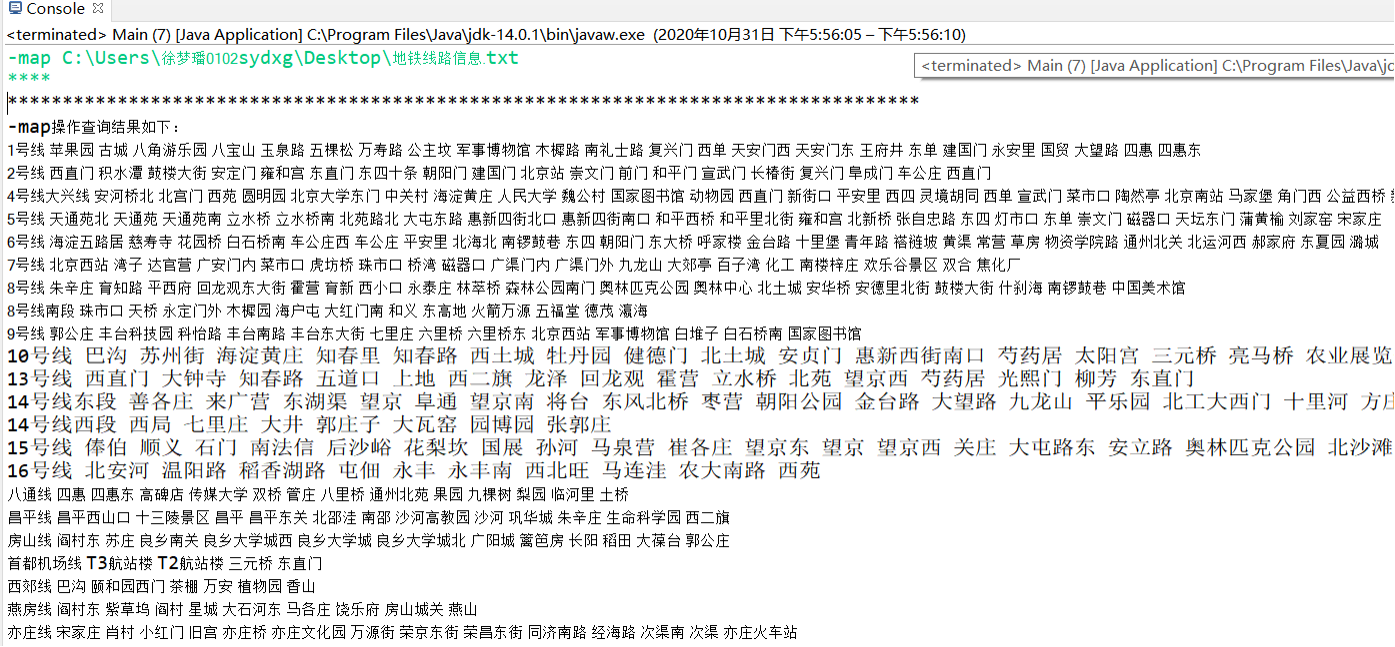
2.-map文件不存在
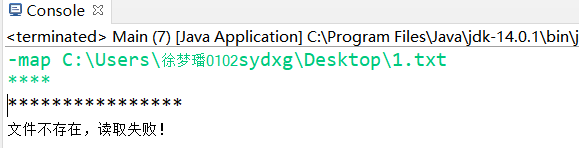
3.-a操作,2号线查询成功,20号线不存在,查询失败


4.-b查询


相应的result.txt文件,也写入了本次查询结果,2号线,10号线有相应的环线标记。

5.-b操作,终止站点不存在


6.-b操作,起始站点不存在


7.-b操作,信息不足


8.-b操作,没有通路(因为试了比较多站点都存在通路,于是自己在文件中写了一条不通的路,来查看没有通路的状况下的提示
添加的没有通路的路线:


9. -b操作





result文件已更新

10.多次多种操作




resul.txt部分截图

- 总结
1.在地铁最短路径实现的过程中,学习到了许多,期间的模式基本是写出基本代码,查询测试正确性,修改错误、不合理。包括在写本文章的测试用例时,也是边发现不足边改正,最后放上了以上测试用例。
2.对于最短路径的实现,虽然可以实现多操作多查询,但是查询的路径可能会有冲突,因为a,b相邻,a可以到b,b也可以到a,但当b已经设定为a的父节点了,下一个查询就不能使a设定为b的父节点了。
-a查询多次查询互不影响。
3.程序可以输出多条最短路径,但可能不是全部的最短路径,因为也会存在第2条所述的冲突,但只要有通路,一定至少会输出一条路径的。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号