数据结构——图
1.思维导图
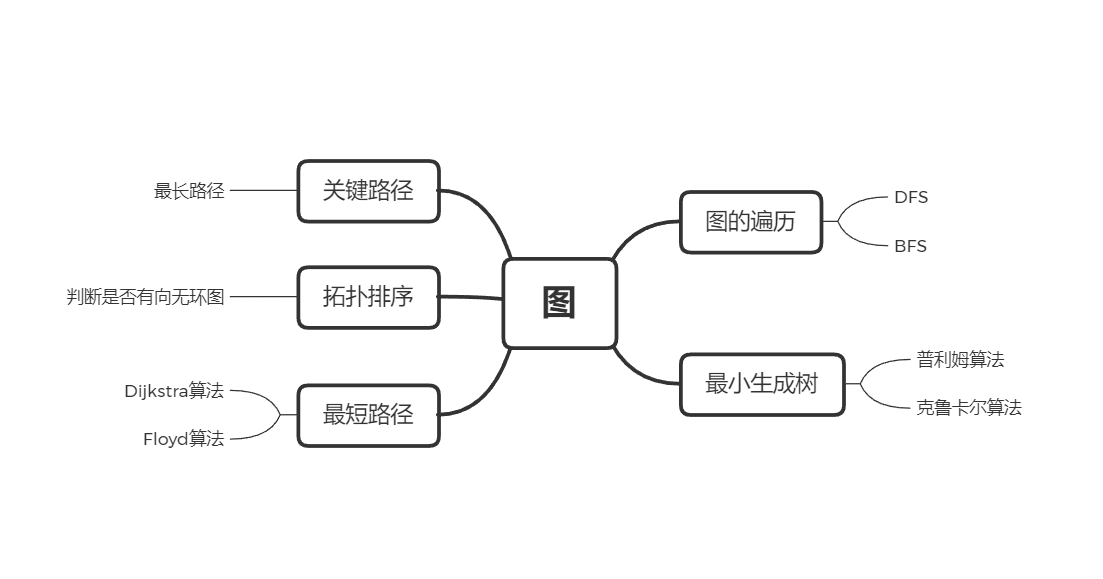
2.重要概念的笔记
1.邻接矩阵与邻接表
邻接矩阵相当于一个二维数组,里面储存相关边的权值,邻接表是由一个表头将相关边通过单链表方式连接
typedef struct //图的定义
{ int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,弧数
} MGraph;
typedef struct ANode
{
int adjvex; //该边的终点编号
struct ANode* nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{
Vertex data; //顶点信息
ArcNode* firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct
{
AdjList adjlist; //邻接表
int n, e; //图中顶点数n和边数e
} AdjGraph;
2.图的遍历——深度遍历DFS算法
DFS算法使用了递归的方式
int i;
visited[v] = 1;
if (flag)cout << " ";
flag = 1;
cout << v;
for (i = 1; i <= g.n; i++) {
if (g.edges[v][i] && !visited[i]) {
DFS(g, i);
}
}
}
3.图的遍历——广度遍历BFS算法
BFS算法运用到了队列的方式储存每一个顶点相连的边
void BFS(MGraph g, int v)
{
int i;
queue<int>q;
q.push(v);
while (!q.empty()) {
if (!flag)cout << " ";
flag = 0;
cout << q.front();
v = q.front();
visited[q.front()] = 1;
for (i = 1; i <= g.n; i++) {
if (g.edges[v][i] && !visited[i]) {
q.push(i);
visited[i] = 1;
}
}
q.pop();
}
}
4.最小生成树——普利姆算法
该算法将每一个点距离已经遍历点合集的最小值储存在一个数组当中,然后遍历数组找到最小值并且加入已遍历的合集中,然后遍历其距离其它顶点的值,将对应的更小值放入数组当中,依次循环n-1次
void prime(MGraph G)
{
int mst[MAXSIZE];
int lowcost[MAXSIZE];
lowcost[0] = 0;
mst[0] = 0;
for (int i = 1; i < G.numvertex; i++)
{
lowcost[i] = G.edges[0][i];
mst[i] = 0;
}
for (int i = 1; i < G.numvertex; i++)
{
int min = INF;
int k = 0;
for (int j = 1; j < G.numvertex; j++)
{
if (lowcost[j] != 0 && lowcost[j] < min)
{
min = lowcost[j];
k = j;
}
}
lowcost[k] = 0;
for (int j = 1; j < G.numvertex; j++)
{
if (lowcost[j] != 0 && G.edges[k][j] < lowcost[j])
{
lowcost[j] = G.edges[k][j];
mst[j] = k;
}
}
}
}
5.最短路径——Dijkstra算法
遍历一个顶点距离其他顶点的值,并且加入到一个数组当中,找到数组中的最小值,遍历该点到其他点的距离,若其他点到原顶点的距离大于原顶点到该点的距离加上该点到其他点的距离,则替换,循环n-1次
void ShortestPath(MyGraph g, int a) {
int Path[MAXV];
int D[MAXV];
int n, i, j;
int k;
int min;
n = g.n;
for (i = 0; i < n; i++) {
visited[i] = 0;
D[i] = g.arcs[a][i];
if (D[i] < INF)Path[i] = a;
else Path[i] = -1;
}
visited[a] = 1;
D[a] = 0;
for (i = 1; i < n; i++) {
min = INF;
for (j = 0; j < n; j++) {
if (!visited[j] && D[j] < min) {
k = j;
min = D[j];
}
}
visited[k] = 1;
for (j = 0; j < n; j++) {
if (!visited[j] && D[k] + g.arcs[k][j] < D[j]) {
Path[j] = k;
D[j] = D[k] + g.arcs[k][j];
}
}
}
}
6.拓扑排序
可以使用栈类来记录入度为零的顶点,并计算先后进入栈的顶点数量,若是和边数相等则是有向无环图
void TopSort(AdjGraph* G) {
int i, j;
int count = 0;
int a[20];
int b[20];
ArcNode* p;
for (i = 0; i < G->n; i++)G->adjlist[i].count = 0;
for (i = 0; i <G-> n; i++) {
p = G->adjlist[i].firstarc;
while (p) {
G->adjlist[p->adjvex].count++;
p = p->nextarc;
}
}
for (i = 0; i < G->n; i++)
if (G->adjlist[i].count == 0)
a[count++]=i;
i=0;
while (count){
j=a[--count];
b[i++]=j;
p = G->adjlist[j].firstarc;
while (p) {
G->adjlist[p->adjvex].count--;
if (!G->adjlist[p->adjvex].count)
a[count++]=p->adjvex;
p = p->nextarc;
}
}
if (i == G->n) {
for (i = 0; i < G->n; i++) {
if (i)cout << " ";
cout << b[i];
}
}
else
cout << "error!";
}
3.疑难问题及解决方案
1.六度空间
该题应该使用广度遍历,且要记录遍历的层数,到六层截止,并记录人数
#define MAXV 1001
#include <iostream>
#include <queue>
using namespace std;
typedef struct ANode
{
int adjvex; //该边的终点编号
struct ANode* nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{
Vertex data; //顶点信息
ArcNode* firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct
{
AdjList adjlist; //邻接表
int n, e; //图中顶点数n和边数e
} AdjGraph;
int visited[MAXV];
int n;
void CreateAdj(AdjGraph*& G, int n, int e); //创建图邻接表
void BFS(AdjGraph* G, int v); //v节点开始广度遍历
int main()
{
cout.setf(ios::fixed);
cout.precision(2);
AdjGraph* G;
int e, i, v,j;
cin >> n >> e;
CreateAdj(G, n, e);
for (i = 1; i <= n; i++) {
BFS(G, i);
for (j = 1; j <= n; j++)visited[j] = 0;
}
}
void CreateAdj(AdjGraph*& G, int n, int e) {
G = new AdjGraph;
ArcNode* p, * q;
int i, j, k;
int a, b;
for (i = 0; i <= n; i++) {
G->adjlist[i].firstarc = NULL;
G->adjlist[i].data = i;
visited[i] = 0;
}
for (i = 0; i < e; i++) {
cin >> a >> b;
p = new ArcNode;
q = new ArcNode;
p->adjvex = b;
q->adjvex = a;
p->nextarc = G->adjlist[a].firstarc;
q->nextarc = G->adjlist[b].firstarc;
G->adjlist[a].firstarc = p;
G->adjlist[b].firstarc = q;
}
G->n = n;
G->e = e;
}
void BFS(AdjGraph* G, int v) {
int i=-1,b;
int a;
double sum = 0;
ArcNode* p;
queue<int>q;
q.push(v);
b = q.back();
visited[v] = 1;
while (!q.empty()&&i<6) {
sum++;
a = q.front();
p = G->adjlist[a].firstarc;
while (p) {
if (!visited[p->adjvex]) {
q.push(p->adjvex);
visited[p->adjvex] = 1;
}
p = p->nextarc;
}
if (q.front() == b) {
b = q.back();
i++;
}
q.pop();
}
cout << v << ": " << sum / n * 100 << "%" << endl;
}
2.旅游规划

该题需要使用到最短路径,同时权值应该同时记录路程及费用两项
#define MAXV 500
#define INF 32767
#include <iostream>
using namespace std;
typedef struct {
int vexs[MAXV];//点的集合
int arcs[MAXV][MAXV];//边的集合
int n, e;
int money[MAXV][MAXV];
}MyGraph;
int visited[MAXV];
void CreateMyG(MyGraph &g, int n, int e);
void ShortestPath(MyGraph g,int a,int b);
int main() {
int n, e, a, b;
int i;
MyGraph g;
cin >> n >> e >> a >> b;
CreateMyG(g, n, e);
ShortestPath(g, a, b);
}
void CreateMyG(MyGraph &g, int n, int e) {
int i, j;
int a, b, c, d;
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
if (j == i) {
g.arcs[i][j] = 0;
g.money[i][j] = 0;
}
else {
g.arcs[i][j] = INF;
g.money[i][j] = INF;
}
}
}
for (i = 0; i < e; i++) {
cin >> a >> b >> c >> d;
g.arcs[a][b] = c;
g.arcs[b][a] = c;
g.money[a][b] = d;
g.money[b][a] = d;
}
g.n = n;
g.e = e;
}
void ShortestPath(MyGraph g, int a, int b) {
int Path[MAXV];
int D[MAXV],E[MAXV];
int n, i, j;
int k;
int min;
n = g.n;
for (i = 0; i < n; i++) {
visited[i] = 0;
D[i] = g.arcs[a][i];
E[i] = g.money[a][i];
if (D[i] < INF)Path[i] = a;
else Path[i] = -1;
}
visited[a] = 1;
D[a] = 0;
for (i = 1; i < n; i++) {
min = INF;
for (j = 0; j < n; j++) {
if (!visited[j] && D[j] < min) {
k = j;
min = D[j];
}
}
visited[k] = 1;
for (j = 0; j < n; j++) {
if (!visited[j] && D[k] + g.arcs[k][j] < D[j]) {
Path[j] = k;
D[j] = D[k] + g.arcs[k][j];
E[j] = E[k] + g.money[k][j];
}
else if (!visited[j] && D[k] + g.arcs[k][j] == D[j]) {
if (E[k] + g.money[k][j] < E[j]) {
E[j] = E[j] = E[k] + g.money[k][j];;
Path[j] = k;
}
}
}
}
cout << D[b] << " " << E[b];
}
3.关键路径
事件的最早发生时间:ve[i]:只有进入Vk的所有活动<Vj, Vi>都结束,Vi代表的事件才能发生,也就是计算前面时间结束的最长时间,而活动<Vj, Vi>的最早结束时间为ve[j]+len<Vj, Vi>。所以,Vi的最早发生时间为:ve[i] = max(ve[j] + len<Vj, Vi>)
事件的最迟发生时间:vl[i]:vl[i]是指在不推迟整个工期的前提下,事件Vi允许的最迟发生时间。所以要找到最长路径<v0, vj>,从Vi出发的活动<Vi, Vj>才能开始,而活动<Vi, Vj>的最晚开始时间为vl[j] - len<Vi, Vj>
活动的最早发生时间:ee[i] ai由有向边<Vk, Vj>,只有顶点Vk代表的事件发生,活动ai才能开始,即活动ai的最早开始时间等于事件Vk的最早开始时间
活动的最迟发生时间:el[i] el[i]是指在不推迟真个工期的前提下,活动ai必须开始的最晚时间。若活动ai由有向边<Vk, Vj>表示,则ai的最晚开始时间要保证事件vj的最迟发生时间不拖后。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号