树、二叉树、查找算法总结
1.思维导图
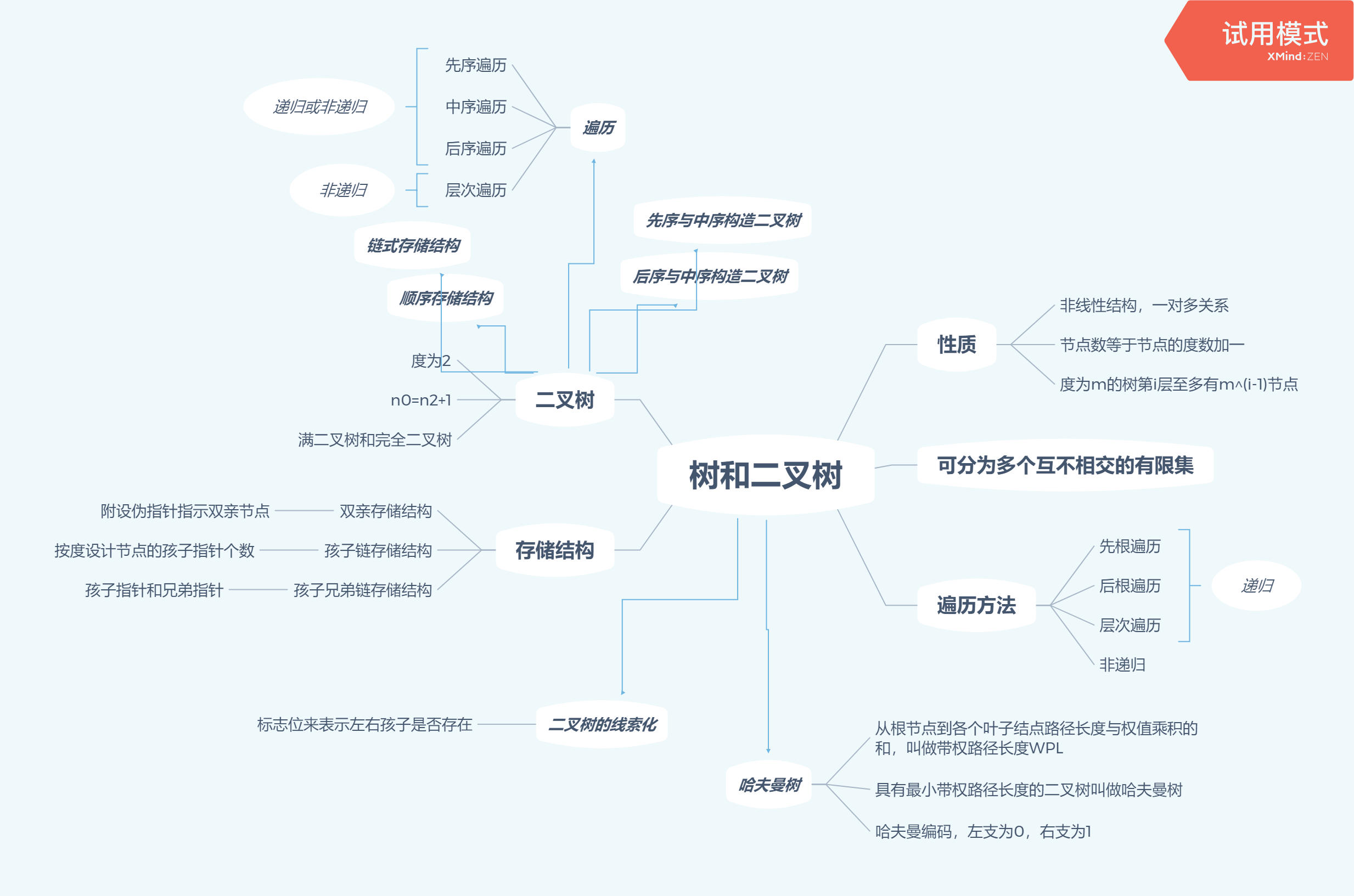
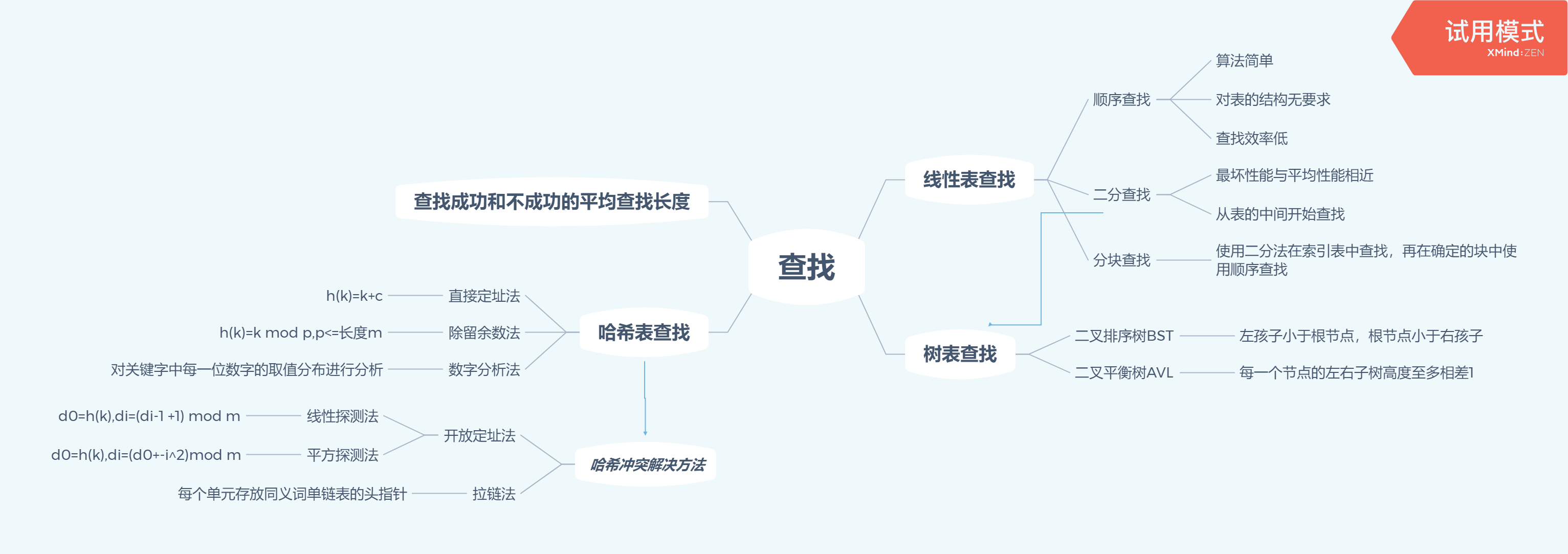
2.重要概念的笔记
1.二叉树的递归遍历
void PreorderPrintLeaves( BinTree BT ){
if(BT!=NULL){
printf(" %c",BT->Data);
PreorderPrintLeaves( BT->Left );
PreorderPrintLeaves( BT->Right );}
}
}
2.二叉树的层次遍历
void Levelorder(BiTree BT) {
BiTree p;
BTqueue q;
int i = 0;
if (BT == NULL) {
cout << "NULL";
return;
}
Crequeue(q);
Enqueue(q, BT);
while (!Emptyqueue(q)) {
Dequeue(q, p);
if (i)cout << " ";
i = 1;
cout << p->data ;
if (p->lchild != NULL) {
Enqueue(q, p->lchild);
}
if (p->rchild != NULL) {
Enqueue(q, p->rchild);
}
}
}
3.二叉树的非递归遍历
void PreOrder(BTree BT) {//非递归先序遍历
BTStack* st;
BTree p;
InitStack(st);
p = BT;
while (!EmptyStack(st) || p != NULL) {
while (p != NILL) {
cout << p->data;
Push(st, p);
p = p->lchild;
}
if (!EmptyStack(st)) {
Pop(st, p);
p = p->rchild;
}
}
}
4.二叉树的构造
BTree creat(int a, int b, int n)//前序遍历和中序遍历构建二叉树
{
BTree T;
int i;
int c;
if (n <= 0) T = NULL;
else
{
T = new BTNode;
T->data = s1[a];
for (i = 0;s1[a] != s2[b + i];i++);
c=a+i;
T->lchild = creat(a + 1, b, i);
T->rchild = creat(c+ 1, b + i + 1, n - i - 1);
}
return T;
}
5.哈夫曼树的算法实现
void CreateHT(HTNode ht[], int n, float s[]) {
int i, j, k, l, r;
float min1, min2;
for (i = 0; i < n; i++) {
ht[i].data = s[i];
}
for (i = n; i < 2 * n - 1; i++) {
min1 = min2 = 32767;
r = l = -1;
for (k = 0; k < i; k++) {
if (ht[k].parent == -1) {
if (ht[k].data < min1) {
min2 = min1;
r = l;
min1 = ht[k].data;
l = k;
}
else if (ht[k].data < min2) {
min2 = ht[k].data;
r = k;
}
}
}
ht[i].data = ht[l].data + ht[r].data;
ht[i].l = l;
ht[i].r = r;
ht[l].parent = ht[r].parent = i;
}
}
6.二叉排序树的构建,插入,查找与删除
InsertBST(T, key) {
if (T为空) {
创建T;
T->data = key;
T的左孩子 = T的右孩子 = 空;
return;
}
else if (T->data = key)
return;
else if (key < T->data)
InsertBST(T->lchild, key);
else if (key > T->data)
InsertBST(T->rchild, key);
}
int InsertBST(BTree& BT, int k) {
if (BT == NULL) {
BT = new BTNode;
BT->data = k;
BT->lchild = BT->rchild = NULL;
return 1;
}
else if (BT->data == k) {
return 0;
}
else if (k < BT->data) {
return InsertBST(BT->lchild, k);
}
else
return InsertBST(BT->rchild, k);
}
BTree SearchBST(BTree BT, int k) {
if (BT == NULL || BT->data == k)
return BT;
if (k < BT->data)
return SearchBST(BT->lchild, k);
else
return SearchBST(BT->rchild, k);
}
void DeleteBST(BTree & BT) {
BTree q, s;
if (BT->lchild == NULL) {
q = BT;
BT = BT->rchild;
delete q;
}
else if (BT->rchild == NULL) {
q = BT;
BT = BT->lchild;
delete q;
}
else {
q = BT;
s = BT->lchild;
while (s->rchild) {
q = s;
s = s->rchild;
}
BT->data = s->data;
if (q == BT)
BT->lchild = s->lchild;
else
q->rchild = s->lchild;
delete s;
}
}
7.二叉平衡树的插入
需要辨别不平衡的最低节点进行调整,观察插入失衡情况进行左左,右右,左右,右左的旋转调整二叉树的平衡。
8.哈希表的构造以及哈希冲突的解决方法
使用直接定址法、除留余数法或者数字分析法进行哈希表的创建排列,当发生哈希冲突时,可使用顺序表的线性探测法和平方探测法,或者使用链表的拉链法将每个单元存放同义词单链表的头指针。
3.疑难问题及解决方案
1.根据后序和中序遍历输出先序遍历

#include<iostream>
#include<string>
using namespace std;
int s1[30];
int s2[30];
typedef struct HTNode {
int data;
struct HTNode* lchild, * rchild;
}HTNode, * HTree;
HTree CreateHT(int a,int b, int n);
void PrintHT(HTree HT);
int main() {
int n, i;
cin >> n;
HTree HT;
HT = new HTNode;
for (i = 0; i < n; i++) {
cin >> s1[i];
}
for (i = 0; i < n; i++) {
cin >> s2[i];
}
HT=CreateHT(n - 1, 0, n);
cout << "Preorder:";
PrintHT(HT);
}
HTree CreateHT(int a, int b, int n) {
HTree T;
int i;
if (n <= 0)T= NULL;
else {
T = new HTNode;
T->data = s1[a];
for (i = 0; s2[b + i] != s1[a]; i++);
T->lchild = CreateHT(a-n+i , b, i);
T->rchild = CreateHT(a - 1 , b + i + 1, n - 1 - i);
}
return T;
}
void PrintHT(HTree HT) {
if (HT != NULL) {
cout << " " << HT->data;
PrintHT(HT->lchild);
PrintHT(HT->rchild);
}
}
该题可以与根据先序遍历和中序遍历创建二叉树联系起来,做一些方位上的修改,就可以比较轻松的完成
2.输出二叉树每层节点
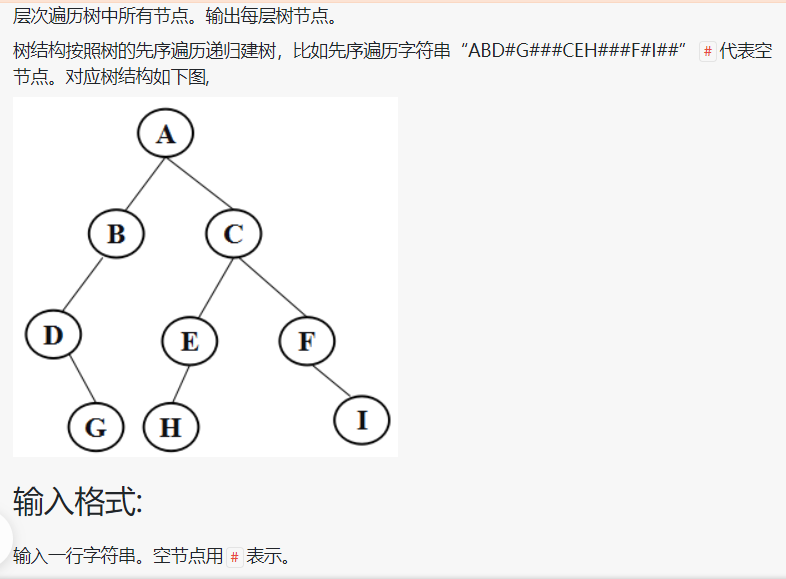
#include<iostream>
#include<string>
#include<queue>
using namespace std;
typedef struct BTNode {
char data;
int h;
struct BTNode* lchild, * rchild;
}BTNode,*BTree;
BTree CreateTree(string s, int& i,int h);
void PrintTree(BTree BT);
int main() {
string s;
int i = 0;
cin >> s;
if(s.size()==0)
cout<<"NULL";
else{
BTree BT;
BT = CreateTree(s, i,1);
if (BT == NULL)cout << "NULL";
else {
PrintTree(BT);
}
}
}
BTree CreateTree(string s, int& i,int h) {
BTree BT;
if (i >= s.size())return NULL;
if (s[i] == '#')return NULL;
BT = new BTNode;
BT->data = s[i];
BT->h = h;
h++;
BT->lchild = CreateTree(s, ++i,h);
BT->rchild = CreateTree(s, ++i,h);
return BT;
}
void PrintTree(BTree BT) {
queue<BTree>q;
BTree p;
int i = 1;
q.push(BT);
cout << i << ":";
while (!q.empty()) {
p = q.front();
if (p->h != i) {
cout << "\n";
i++;
cout << i << ":";
}
cout << p->data << ",";
q.pop();
if (p->lchild != NULL)
q.push(p->lchild);
if (p->rchild != NULL) {
q.push(p->rchild);
}
}
}
灵活使用层次遍历
3.二叉树的线索化如何实现
简而言之就是当该节点非头结点时,若左孩子为空,则左指针指向前驱节点,若右孩子为空,则右指针指向后继节点。在遍历线索二叉树时,若找不到后继节点,则寻找右孩子节点的最左孩子节点,否则就跟随后继节点,直到后继节点指向头结点。
4.哈夫曼树

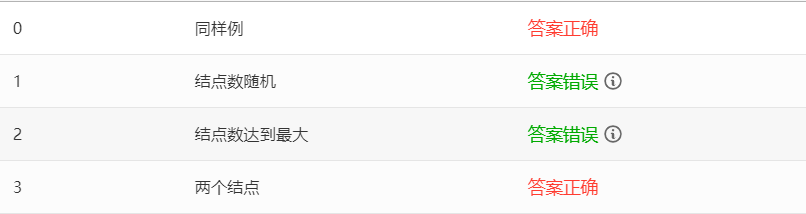
目前找不到中间两个测试点出错的原因在哪
#include<iostream>
#include<string>
using namespace std;
#define MAX 20000
typedef struct HTNode {
float data;
int l = -1;
int r = -1;
int parent = -1;
}HTNode, * HTree;
void CreateHT(HTNode ht[], int n, float s[]);
float Count(HTNode ht[], int n);
int main() {
int n, i;
cin >> n;
float s[10000];
for (i = 0; i < n; i++) {
cin >> s[i];
}
HTNode ht[MAX];
HTree head;
CreateHT(ht, n, s);
cout << Count(ht, n);
}
void CreateHT(HTNode ht[], int n, float s[]) {
int i, j, k, l, r;
float min1, min2;
for (i = 0; i < n; i++) {
ht[i].data = s[i];
}
for (i = n; i < 2 * n - 1; i++) {
min1 = min2 = 32767;
r = l = -1;
for (k = 0; k < i; k++) {
if (ht[k].parent == -1) {
if (ht[k].data < min1) {
min2 = min1;
r = l;
min1 = ht[k].data;
l = k;
}
else if (ht[k].data < min2) {
min2 = ht[k].data;
r = k;
}
}
}
ht[i].data = ht[l].data + ht[r].data;
ht[i].l = l;
ht[i].r = r;
ht[l].parent = ht[r].parent = i;
}
}
float Count(HTNode ht[], int n) {
int i;
float sum = 0;
for (i = 0; i < 2*n-2; i++) {
sum += ht[i].data ;
}
return sum;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号