Si-SiO2界面态密度的研究

本文以MIS基本结构为例, 探究其一个重要的物理参数——界面态密度. 将讲述器件中的界面态形成的机理, 现实工艺中如何降低器件中的界面态密度, 最后讲述实验中如何测量界面态电容.

以常见的硅晶体来说, 在晶体的表面会存在未饱和的悬挂键, 特别注意, 不同表面对应了不同硅晶体的晶面, 不同方向的表面其悬挂键的密度会不同. 并且晶体表面悬挂键的密度很高, 且悬挂键之间存在相互作用. 我们知道, 悬挂键是一个未饱和的电子, 因此晶体表面会形成表面能带, 进而在晶体表面处有界面态密度的概念.

图 1硅晶体结构示意图

界面态可以起产生、复合中心作用，使pn结反向漏电流增加、双极性晶体管小电流时电流增益下降、产生1/f噪声等. 界面态还可以起到散射中心作用，使MOS晶体管跨导降低、频率特性和开关特性变差、阈值电压不稳定.

我们知道, 现实中拥有理想表面的理想晶体是不存在的. 晶体的表面会有各种各样的缺陷. 集成电路制造中，掺杂工艺可以改变半导体原有电性；但是掺杂原子是强行注入，会对半导体表面形成损伤, 频繁的电离辐射损伤会产生介面缺陷导致界面态密度增加.

因此在半导体工艺中, 需要不断对半导体相关器件进行退火处理以期待降低其界面态密度, 同时还需要再每道工艺结束后及时跟进测量界面态密度的大小, 使得对器件的性能有一个把控. 以下先来讲述实际退火工艺.

"退火"最初是在金属加工里提及，金属加温并维持此温度一段时间，再将其缓慢冷却，增加柔软性、延展性和韧性. 实际晶体是由一个个小小的"晶粒"组成，晶粒之间的接触边缘称为"晶界", 这些晶界可以让原子不容易错位，所以多晶体结构反而比单纯的晶体更有韧性；如果晶粒越大，那么原子间容易换位移动就会形成比较软的物性.

图 2微电子器件电镜图

退火可以修复器件缺陷并改变器件的界面态密度的机理, 从晶体学角度：晶粒的大小可以用降温速度来控制，加热到晶体原子能够重新排列的温度后，保温一段时间，然后缓慢降温，晶粒就可以慢慢生长到比较大的样子，这样就可以让金属变软，加工后残余的应力也降低; 从固体电子学角度：在热处理时，晶圆温度较高，原子的振动能级大，移动能力增强，因而可以使复杂的损伤分解为简单的缺陷，例如空位和间隙原子等。

目前, 常见的退火工艺有三种, 分别是炉管退火(Furnace Anneal), 快速热退火(RTP), 毫秒级的退火工艺.

从图3(a)看出, 扩散炉退火是在充满惰性气体的环境下在700-1200℃的高温范围内保持一段时间；并且扩散炉闲置时的温度仍然维持在400-700℃. 从图3(b)可以看出晶格缺陷在退火时, 其热积存效应和杂质扩散变得显著, 长时间的退火会导致离子注入分布严重偏离期望分布.

图 3炉管退火工艺参数图

实际退火工艺中, 晶圆器件在进出扩散炉的时候应该动作缓慢, 避免热应力导致晶圆弯曲. 但缓慢进出的过程会使得晶圆载舟的两端会有不同的退火时间, 从而导致晶圆退火的时间不均匀. 这种副效应对于小尺寸的器件来讲已经威胁到其器件的正常工作. 因此在实际工艺中, 随着技术节点缩短到$0.13\mathrm{\mu m}$以下或者是$45\mathrm{nm}$以下, 就需要用快速热退火(RTP).

图 4 RTP工艺参数图

从图4可以看出, 对于RTP退火工艺来讲, 由于加热的时间相对较短, 不仅可以修复晶格损伤, 而且注入的原子分布基本不变. 其特点由于是单片式作业, 可以良好地坐到较好均一性和稳定性.

那么, 实验中如何测量相关器件的界面态密度呢?

以常见的MIS基本结构为例.

图 5 MIS基本结构

如图, 在器件栅极加上栅电压$V_{\mathrm{G}}$, 则半导体表面电压降$V_S$和绝缘层电压降$V_{OX}$之间的关系为$V_G=V_{OX}+V_S$. 在理想情况下, 绝缘层电场均匀, 则$V_0=E_0d$. 由高斯定理得到金属表面的面电荷$Q_M=\epsilon _{I0}\epsilon _0E_0$. 又因为半导体表面电荷满足$Q_S=-Q_M$, 且$C_0=\frac{\epsilon _{I0}\epsilon _0E_0}{E_0d_0}=\frac{\epsilon _{I0}\epsilon _0}{d_0}$. 于是得到绝缘层电压和栅电压为:

$$V_0=-\frac{Q_S}{C_{OX}}$$

$$V_G=-\frac{Q_S}{C_{OX}}+V_S$$

当有小信号电压$\mathrm{d}V_G=-\mathrm{d}Q_S/C_{OX}+\mathrm{d}V_S$作用于MIS结构时, 根据微分电容定义可以得到$C=\mathrm{d}Q_M/\mathrm{d}V_G=-\mathrm{d}Q_S/\mathrm{d}V_G$, 两式联立得到MIS结构的电容为:

$$\frac{1}{C}=\frac{1}{C_{OX}}+\frac{1}{C_S}$$

因此, MIS结构的电容相当于绝缘层电容和半导体空间电荷层电容的串联.

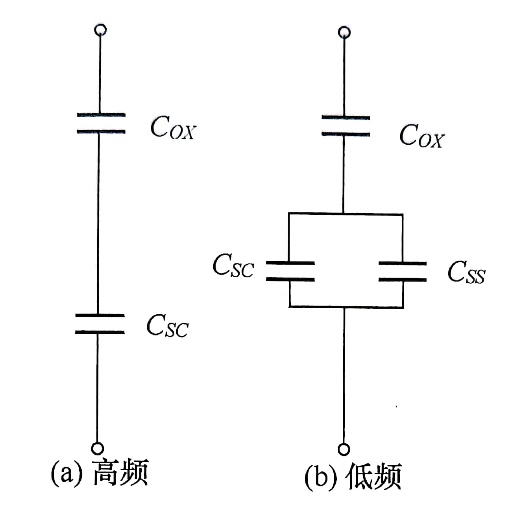
图 6 MOS结构等效电路

以金属—二氧化硅—硅的MOS结构作为实验样品, 在高频信号作用下的等效电路如图6(a)所示. 图中$C_{OX}$是氧化层电容、$C_{SC}$是半导体空间电荷区电容. 因为界面态的充放电跟不上高频信号的变化, 在等效电路中九不出现与界面态有关的电容. 如果测量的信号频率及直流偏压的变化足够慢, 使界面态的充放电始终跟得上电压的变化, 则必须考虑界面态电容的影响, 图6(b)即MOS结构的低频等效电路, 图中$C_{SS}$是界面态电容. 因此在高频和低频时, 其电容关系为:

$$\begin{cases} \frac{1}{C_{LF}}=\frac{1}{C_{OX}}+\frac{1}{C_{SC}+C_{SS}}\\ \frac{1}{C_{HF}}=\frac{1}{C_{OX}}+\frac{1}{C_{SC}}\\\end{cases}$$

联立消去$C_{SC}$得到:

$$\begin{aligned} C_{SS}&=\frac{C_{LF}C_{ox}}{C_{OX}-C_{LF}}-\frac{C_{HF}C_{ox}}{C_{OX}C_{HF}}\\ &=C_{ox}\left[ \frac{C_{LF}/C_{OX}}{1-\left( C_{LF}/C_{OX} \right)}-\frac{C_{HF}/C_{OX}}{1-\left( C_{HF}/C_{OX} \right)} \right]\\\end{aligned}$$

因为界面态密度定义为单位面积, 单位能量间隔内的界面态能级数, 因此, 当表面势变化$\mathrm{d}V_S$时, 界面态中电荷的变化量为:

$$\mathrm{d}Q_{SS}=\mathrm{A}_mqN_{SS}\mathrm{dV}_S$$

式中, $A_m$为MOS结构金属电极面积. 则界面态密度

$$N_{SS}=\frac{1}{A_m}\cdot \frac{1}{q}\cdot \frac{\mathrm{d}Q_{SS}}{\mathrm{d}V_s}=\frac{1}{\mathrm{A}_m}\cdot \frac{C_{\mathrm{SS}}\left( V_S \right)}{q}$$

从以上推导可以看出界面态密度$N_{SS}$与半导体表面势$V_S$有关. 实际我们更关心与栅电压$V_g$之间的关系, 这是因为栅电压式直接可测量量. 因此, 我们还需要求出$V_S—V_g$之间的关系.

对于金属的感应电荷和半导体的空间电荷等量可以得到:

$$\mathrm{d}Q_{\mathrm{M}}=C_{OX}\mathrm{d}V_{OX}=C_{LF}\left( V_g \right) \cdot \mathrm{d}V_g$$

则$V_S—V_g$关系为

$$\mathrm{d}V_S=\mathrm{d}V_g-\mathrm{d}V_{OX}=\mathrm{d}V_g-\frac{C_{LF}\left( V_g \right)}{C_{OX}}\mathrm{d}V_g=\left[ 1-\frac{C_{LF}\left( V_g \right)}{C_{ox}} \right] dV_g$$

因为半导体在平带($V_g=V_{FB}$)位置表面势$V_S=0$, 积分得到:

$$V_S\left( V_g \right) =\int_{V_{FB}}^{V_g}{\left[ 1-\frac{C_{LF}\left( V_g\prime \right)}{C_{ox}} \right]}dV_g\prime$$

图 7PMOS结构在高频和低频下归一化C-V曲线

实验中, 对栅电压$V_X\left( V_G \right) $进行调节频率和大小, 可以得到器件在高频和低频时的电容变化情况, 代入式(5), 即可得到$C_{SS}—V_G$的关系. 接着联立式(7)最终得到界面态密度与栅电压$V_G$的关系.