霍夫线变换(霍夫变换检测直线)
霍夫线变换
原理¶
Note
以下原理的说明来自书籍 学习OpenCV 作者Bradski和Kaehler.
霍夫线变换
- 霍夫线变换是一种用来寻找直线的方法.
- 是用霍夫线变换之前, 首先要对图像进行边缘检测的处理,也即霍夫线变换的直接输入只能是边缘二值图像.
它是如何实现的?
-
众所周知, 一条直线在图像二维空间可由两个变量表示. 例如:
- 在 笛卡尔坐标系: 可由参数:
![(m,b)]() 斜率和截距表示.
斜率和截距表示. - 在 极坐标系: 可由参数:
![(r,\theta)]() 极径和极角表示
极径和极角表示
![Line variables]()
对于霍夫变换, 我们将用 极坐标系 来表示直线. 因此, 直线的表达式可为:
![y = \left ( -\dfrac{\cos \theta}{\sin \theta} \right ) x + \left ( \dfrac{r}{\sin \theta} \right )]()
化简得:
![r = x \cos \theta + y \sin \theta]()
- 在 笛卡尔坐标系: 可由参数:
-
一般来说对于点
![(x_{0}, y_{0})]() , 我们可以将通过这个点的一族直线统一定义为:
, 我们可以将通过这个点的一族直线统一定义为:![r_{\theta} = x_{0} \cdot \cos \theta + y_{0} \cdot \sin \theta]()
这就意味着每一对
![(r_{\theta},\theta)]() 代表一条通过点
代表一条通过点 ![(x_{0}, y_{0})]() 的直线.
的直线. -
如果对于一个给定点
![(x_{0}, y_{0})]() 我们在极坐标对极径极角平面绘出所有通过它的直线, 将得到一条正弦曲线. 例如, 对于给定点
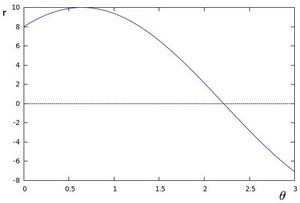
我们在极坐标对极径极角平面绘出所有通过它的直线, 将得到一条正弦曲线. 例如, 对于给定点 ![x_{0} = 8]() and
and ![y_{0} = 6]() 我们可以绘出下图 (在平面
我们可以绘出下图 (在平面 ![\theta]() -
- ![r]() ):
):![Polar plot of a the family of lines of a point]()
只绘出满足下列条件的点
![r > 0]() and
and ![0< \theta < 2 \pi]() .
. -
我们可以对图像中所有的点进行上述操作. 如果两个不同点进行上述操作后得到的曲线在平面
![\theta]() -
- ![r]() 相交, 这就意味着它们通过同一条直线. 例如, 接上面的例子我们继续对点:
相交, 这就意味着它们通过同一条直线. 例如, 接上面的例子我们继续对点: ![x_{1} = 9]() ,
, ![y_{1} = 4]() 和点
和点 ![x_{2} = 12]() ,
, ![y_{2} = 3]() 绘图, 得到下图:
绘图, 得到下图:![Polar plot of the family of lines for three points]()
这三条曲线在
![\theta]() -
- ![r]() 平面相交于点
平面相交于点 ![(0.925, 9.6)]() , 坐标表示的是参数对 (
, 坐标表示的是参数对 (![\theta, r]() ) 或者是说点
) 或者是说点 ![(x_{0}, y_{0})]() , 点
, 点 ![(x_{1}, y_{1})]() 和点
和点 ![(x_{2}, y_{2})]() 组成的平面内的的直线.
组成的平面内的的直线. -
那么以上的材料要说明什么呢? 这意味着一般来说, 一条直线能够通过在平面
![\theta]() -
- ![r]() 寻找交于一点的曲线数量来 检测. 越多曲线交于一点也就意味着这个交点表示的直线由更多的点组成. 一般来说我们可以通过设置直线上点的 阈值 来定义多少条曲线交于一点我们才认为 检测 到了一条直线.
寻找交于一点的曲线数量来 检测. 越多曲线交于一点也就意味着这个交点表示的直线由更多的点组成. 一般来说我们可以通过设置直线上点的 阈值 来定义多少条曲线交于一点我们才认为 检测 到了一条直线. -
这就是霍夫线变换要做的. 它追踪图像中每个点对应曲线间的交点. 如果交于一点的曲线的数量超过了 阈值, 那么可以认为这个交点所代表的参数对
![(\theta, r_{\theta})]() 在原图像中为一条直线.
在原图像中为一条直线.
标准霍夫线变换和统计概率霍夫线变换
OpenCV实现了以下两种霍夫线变换:
- 标准霍夫线变换
- 原理在上面的部分已经说明了. 它能给我们提供一组参数对
的集合来表示检测到的直线
- 在OpenCV 中通过函数 HoughLines 来实现
- 统计概率霍夫线变换
- 这是执行起来效率更高的霍夫线变换. 它输出检测到的直线的端点
- 在OpenCV 中它通过函数 HoughLinesP 来实现
代码
- 这个程序是用来做什么的?
- 加载一幅图片
- 对图片进行 标准霍夫线变换 或是 统计概率霍夫线变换.
- 分别在两个窗口显示原图像和绘出检测到直线的图像.
- 我们将要说明的例程能从 这里 下载。 一个更高级的版本 (能同时演示标准霍夫线变换和统计概率霍夫线变换并带有活动条来改变变换的阈值) 能从 这里 下载。
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include <iostream>
using namespace cv;
using namespace std;
void help()
{
cout << "\nThis program demonstrates line finding with the Hough transform.\n"
"Usage:\n"
"./houghlines <image_name>, Default is pic1.jpg\n" << endl;
}
int main(int argc, char** argv)
{
const char* filename = argc >= 2 ? argv[1] : "pic1.jpg";
Mat src = imread(filename, 0);
if(src.empty())
{
help();
cout << "can not open " << filename << endl;
return -1;
}
Mat dst, cdst;
Canny(src, dst, 50, 200, 3);
cvtColor(dst, cdst, CV_GRAY2BGR);
#if 0
vector<Vec2f> lines;
HoughLines(dst, lines, 1, CV_PI/180, 100, 0, 0 );
for( size_t i = 0; i < lines.size(); i++ )
{
float rho = lines[i][0], theta = lines[i][1];
Point pt1, pt2;
double a = cos(theta), b = sin(theta);
double x0 = a*rho, y0 = b*rho;
pt1.x = cvRound(x0 + 1000*(-b));
pt1.y = cvRound(y0 + 1000*(a));
pt2.x = cvRound(x0 - 1000*(-b));
pt2.y = cvRound(y0 - 1000*(a));
line( cdst, pt1, pt2, Scalar(0,0,255), 3, CV_AA);
}
#else
vector<Vec4i> lines;
HoughLinesP(dst, lines, 1, CV_PI/180, 50, 50, 10 );
for( size_t i = 0; i < lines.size(); i++ )
{
Vec4i l = lines[i];
line( cdst, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(0,0,255), 3, CV_AA);
}
#endif
imshow("source", src);
imshow("detected lines", cdst);
waitKey();
return 0;
}
代码说明
-
加载图片
Mat src = imread(filename, 0); if(src.empty()) { help(); cout << "can not open " << filename << endl; return -1; } -
用Canny算子对图像进行边缘检测
Canny(src, dst, 50, 200, 3);现在我们将要执行霍夫线变换. 我们将会说明怎样使用OpenCV的函数做到这一点:
-
标准霍夫线变换
-
首先, 你要执行变换:
vector<Vec2f> lines; HoughLines(dst, lines, 1, CV_PI/180, 100, 0, 0 );带有以下自变量:
- dst: 边缘检测的输出图像. 它应该是个灰度图 (但事实上是个二值化图)
- lines: 储存着检测到的直线的参数对
![(r,\theta)]() 的容器 * rho : 参数极径
的容器 * rho : 参数极径 ![r]() 以像素值为单位的分辨率. 我们使用 1 像素.
以像素值为单位的分辨率. 我们使用 1 像素. - theta: 参数极角
![\theta]() 以弧度为单位的分辨率. 我们使用 1度 (即CV_PI/180)
以弧度为单位的分辨率. 我们使用 1度 (即CV_PI/180) - threshold: 要”检测” 一条直线所需最少的的曲线交点
- srn and stn: 参数默认为0. 查缺OpenCV参考文献来获取更多信息.
-
通过画出检测到的直线来显示结果.
for( size_t i = 0; i < lines.size(); i++ ) { float rho = lines[i][0], theta = lines[i][1]; Point pt1, pt2; double a = cos(theta), b = sin(theta); double x0 = a*rho, y0 = b*rho; pt1.x = cvRound(x0 + 1000*(-b)); pt1.y = cvRound(y0 + 1000*(a)); pt2.x = cvRound(x0 - 1000*(-b)); pt2.y = cvRound(y0 - 1000*(a)); line( cdst, pt1, pt2, Scalar(0,0,255), 3, CV_AA); }
-
-
统计概率霍夫线变换
-
首先, 你要执行变换:
vector<Vec4i> lines; HoughLinesP(dst, lines, 1, CV_PI/180, 50, 50, 10 );带有以下自变量:
- dst: 边缘检测的输出图像. 它应该是个灰度图 (但事实上是个二值化图) * lines: 储存着检测到的直线的参数对
![(x_{start}, y_{start}, x_{end}, y_{end})]() 的容器
的容器 - rho : 参数极径
![r]() 以像素值为单位的分辨率. 我们使用 1 像素.
以像素值为单位的分辨率. 我们使用 1 像素. - theta: 参数极角
![\theta]() 以弧度为单位的分辨率. 我们使用 1度 (即CV_PI/180)
以弧度为单位的分辨率. 我们使用 1度 (即CV_PI/180) - threshold: 要”检测” 一条直线所需最少的的曲线交点 * minLinLength: 能组成一条直线的最少点的数量. 点数量不足的直线将被抛弃.
- maxLineGap: 能被认为在一条直线上的亮点的最大距离.
- dst: 边缘检测的输出图像. 它应该是个灰度图 (但事实上是个二值化图) * lines: 储存着检测到的直线的参数对
-
通过画出检测到的直线来显示结果.
for( size_t i = 0; i < lines.size(); i++ ) { Vec4i l = lines[i]; line( cdst, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(0,0,255), 3, CV_AA); }
-
-
显示原始图像和检测到的直线:
imshow("source", src); imshow("detected lines", cdst); -
等待用户按键推出程序
waitKey();
结果¶
Note
得到的结果使用的是在上面 代码 部分提到的更高级版代码. 霍夫线变换的代码没有改变, 唯一不同的是在GUI的部分加入了活动条可动态改变阈值.输入图像为:

通过执行统计概率霍夫线变换我们能得到下面的结果:
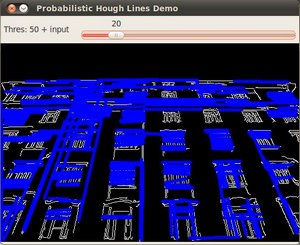
当你使用滑动条来改变 阈值 的时候会观察到检测到线的数目的改变. 这是因为: 如果你设置了一个更大的阈值, 能检测到的线的数目将更少 (你需要更多的点来表示一条能检测到的直线).



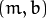 斜率和截距表示.
斜率和截距表示.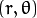 极径和极角表示
极径和极角表示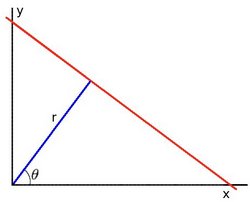
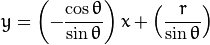
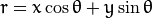
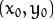 , 我们可以将通过这个点的一族直线统一定义为:
, 我们可以将通过这个点的一族直线统一定义为: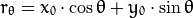
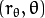 代表一条通过点
代表一条通过点 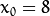 and
and 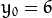 我们可以绘出下图 (在平面
我们可以绘出下图 (在平面 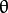 -
- 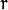 ):
):
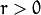 and
and 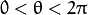 .
.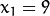 ,
, 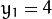 和点
和点 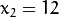 ,
, 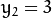 绘图, 得到下图:
绘图, 得到下图: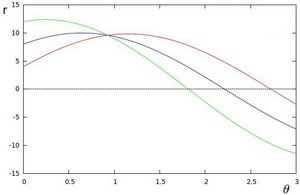
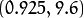 , 坐标表示的是参数对 (
, 坐标表示的是参数对 (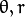 ) 或者是说点
) 或者是说点 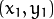 和点
和点 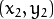 组成的平面内的的直线.
组成的平面内的的直线.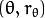 在原图像中为一条直线.
在原图像中为一条直线.
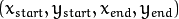 的容器
的容器
 浙公网安备 33010602011771号
浙公网安备 33010602011771号