binarytree

1. 二叉树简介

2. 二叉树实现代码及boost类库中对于图的支持简单介绍

3. 代码反思 

4. 代码下载

1. 二叉树简介

 二叉树顾名思义，除了叶子节点之外，每个节点均含有两个子节点。例如：

 

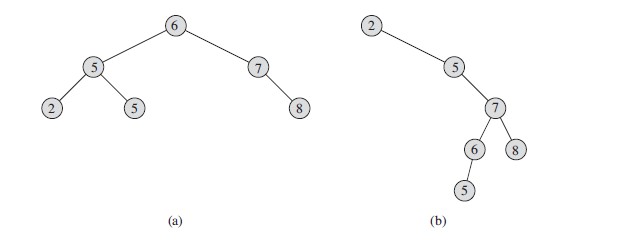
二叉查找树是满足下面的下面条件的 二叉树：

 

下面定义在二叉查找树上的操作：

1. 二叉查找树上最大元素：maxElement 

2. 最小元素：minElement 

3. 前序遍历：preOrder 

4. 中序遍历： inOrder

5. 后序遍历：postOrder 

6.  中序遍历的前驱：precursor

7. 中序遍历后继：successor 

8. 插入节点：insertNode

9. 删除节点：deleteNode 

2. 二叉树实现算法

代码量比较大，这里略去代码，仅仅是描述算法的思想。下面有完整的代码下载。 

2.1. 析构函数主要负责将释放内存，主要的算法是树的后序（注意只能使用后序遍历算法）遍历算法。

2.2 遍历算法主要是通过递归实现，递归的结束条件也是比较简单。

 

2.3 中序遍历的后继，对于下面的二叉树来说的话，分为下面的集中情况：1. 如果存在右节点的话，那么后继就是右节点的的最左孩子，如图中的1节点. 2. 没有右孩子，并且是作为左孩子出现的话，那么该节点的父节点就是后继结点，如下图中的4节点。3. 如果该节点没有右孩子，同时作为右孩子出现的话，需要向上回溯，直到找到第一个作为左孩子的父节点，如图中的9节点。

 

 

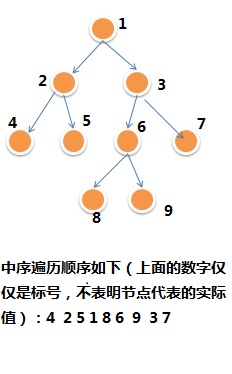
2.4 中序遍历的前驱：1. 有左孩子的话，直接返回左孩子；2.没有左孩子，并且该节点是作为右孩子的话，返回父节点；3.没有左孩子，并且是作为左孩子的话，寻找第一个作为右孩子的父节点。

2.5  插入节点：首先通过循环查找到新插入节点的位置（父节点），然后将数据插入即可，但是这里需要判定当前树是否为空。

2.6 删除节点分为下面的集中情况（常见代码）：

 

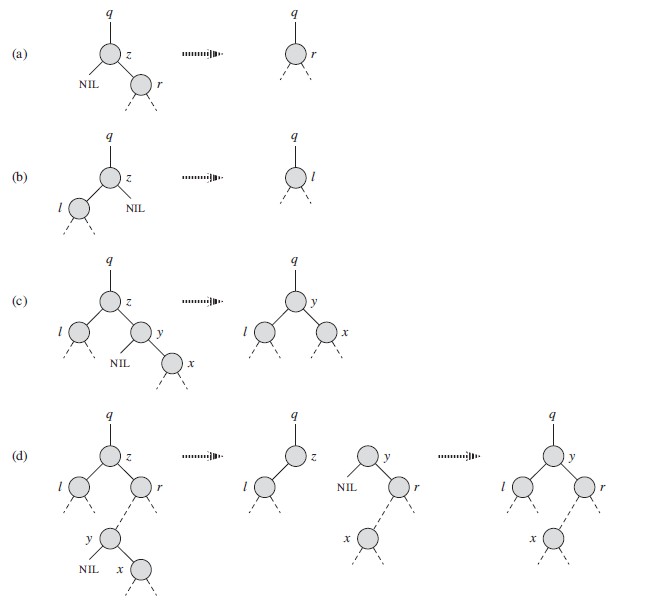
3. 代码反思

3.1 由于树在定义时就是使用递归定义的，所以树的很多问题都能通过递归实现，例如在析构函数释放内存，代码如下：

---

// 析构函数

    // 释放内存

    void FreeMem(MyBinaryTreeNode* node)

    {

        // 递归结束条件

         if (node == NULL)

            return;

        FreeMem(node->left());

        FreeMem(node->right());

        delete node;

    }

---

3.2 在树的算法的实现中，存在很多情况下使用双游标的情况。例如在insertNode中为了找到新加入的节点的父节点，通过如下的代码实现：

---

   MyBinaryTreeNode* parent = NULL;

        MyBinaryTreeNode* child = m_pRoot;

        // 新插入的元素一定是在树叶下插入

        while( (child != NULL) )

        {

            parent = child;

            // 开始移动

            if (child->value() > ele->value())

                child = child->left();

            else

            {

                child = child->right();

            }

        }

---

4.代码下载 

 /Files/xuqiang/algorithm/MyBinaryTree.rar