BresenHam算法画直线

实验原理

程序步骤

①画起点(x1,y1)
②准备画下一个点，X坐标加1，判断如果达到终点，则完成。否则找下一个点，由图可知要画的点要么为当前点的右邻接点，要么是当前点的右上邻接点。
（1）如果线段ax+by+c=0与x=x1+1的交点y坐标大于(y+*y+1))/2则选右上那个点。
（2）否则选右下那个点。
③画点
④回到第二步
⑤结束

算法伪代码：

ξ ← 0, y ← y1
            For x ← x1 to x2 do
                Plot Point at (x, y)
                If (2(ξ + dy) < dx)
                    ξ ←ξ + dy
                Else
                    y ← y + 1,ξ ←ξ + dy – dx
                End If
            End For

实验环境

Microsoft Windows 11
Anaconda python 3.11.9
matplotlib

完整代码

import matplotlib.pyplot as plt
def bresenham_line(ax, x1, y1, x2, y2):
    dx = abs(x2 - x1)
    dy = abs(y2 - y1)
    sx = 1 if x1 < x2 else -1
    sy = 1 if y1 < y2 else -1
    err = dx - dy
    while True:
        ax.plot(x1, y1, 'o')
        if x1 == x2 and y1 == y2:
            break
        e2 = 2 * err
        if e2 > -dy:
            err -= dy
            x1 += sx
        if e2 < dx:
            err += dx
            y1 += sy
fig, ax = plt.subplots()
x1, y1 = 10, 10
x2, y2 = 300, 300
bresenham_line(ax, x1, y1, x2, y2)
ax.set_xlim(0, 400)
ax.set_ylim(0, 400)
plt.show()

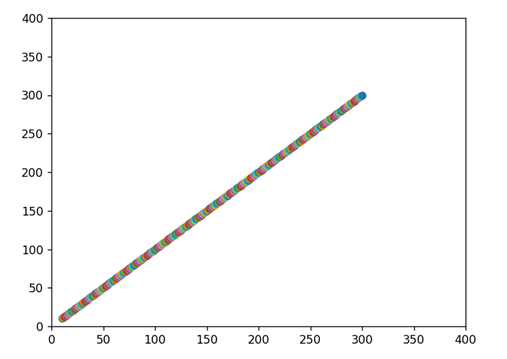
实验结果

可以高效完成直线的绘制，并且在视觉上可以观察到绘制的直线是平滑的。表现出了良好的准确性。

实验分析

Bresenham算法由于其高效性和准确性，在计算机图形学和图像处理领域有着广泛的应用。例如，在需要快速绘制大量直线的图形渲染中，Bresenham算法可以显著提高渲染性能。此外，在进行图像分割、直线特征提取等图像处理任务时，Bresenham算法也是优选的算法之一。
算法主要适用于栅格图形，对于非栅格或抗锯齿的图形处理可能不是最佳选择。