腾讯expLTV建模用户LTV《Out of the Box Thinking: Improving Customer Lifetime Value Modelling via Expert Routing and Game Whale Detection》
背景
在游戏付费场景里,少部分的用户贡献了大部分的收益,论文中把这少部分高价值用户称为“游戏鲸鱼用户”,分析数据发现游戏鲸鱼用户和普通用户的LTV分布不同,因此腾讯在google ZILN 论文基础上提出了用多专家门控网络来分人群建模游戏鲸鱼用户和普通用户的的LTV
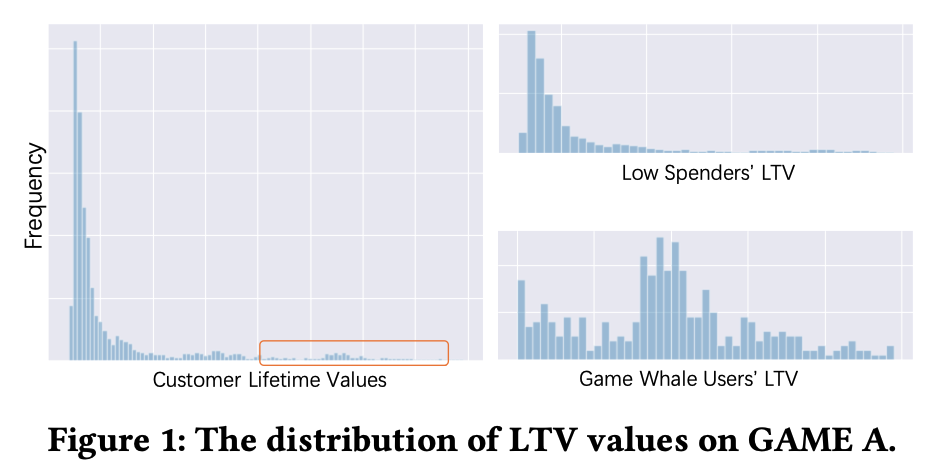
相关定义
游戏鲸鱼用户的购买概率:
\[ p_{u}^{gwptr} = p(g_{u}=1, s_{u}=1|\mathbf{x}_{u}) = 1 - e^{\frac{-LTV_{u}}{R}} \]
其中\( g_{u} = 1 \)表示该用户是游戏鲸鱼用户,\( s_{u} = 1 \)表示该用户发生购买行为,如果LTV大于等于R,那么该用户被定义为游戏鲸鱼用户
注意,当且仅当 \(LTV_{u} = 0\) 时,\( p_{u}^{gwptr} = 0\)
用户是游戏鲸鱼用户的概率(用户是游戏鲸鱼用户前提是发生过购买行为):
\[ p_{u}^{gw} = p(g_{u} = 1 | s_{u} = 1, \mathbf{x}_{u}) \]
根据上面两个式子可以推导出游戏鲸鱼用户的购买概率和普通用户的购买概率:
\[ \begin{align*} \hat{p}_{u}^{gwptr} &= p(g_{u} = 1, s_{u} = 1|\mathbf{x}_{u}) \\ &= p(s_{u} = 1|\mathbf{x}_{u}) \times p(g_{u} = 1|s_{u} = 1, \mathbf{x}_{u}) \\ &= \hat{p}_{u}^{ptr} \times \hat{p}_{u}^{gw}, \end{align*} \]
\[ \begin{align*} \hat{p}_{u}^{ngwptr} &= p(g_{u} = 1, s_{u} = 0|\mathbf{x}_{u}) + p(g_{u} = 0, s_{u} = 1|\mathbf{x}_{u}) \\ &\quad + p(g_{u} = 0, s_{u} = 0|\mathbf{x}_{u}) \\ &= p(s_{u} = 0|\mathbf{x}_{u}) + p(s_{u} = 1|\mathbf{x}_{u})p(g_{u} = 0|s_{u} = 1, \mathbf{x}_{u}) \\ &= (1 - \hat{p}_{u}^{ptr}) + \hat{p}_{u}^{ptr} \times \hat{p}_{u}^{ngw}, \end{align*} \]
其中:\[ \hat{p}_{u}^{ptr} = p(s_{u} = 1|\mathbf{x}_{u}), \]
模型架构
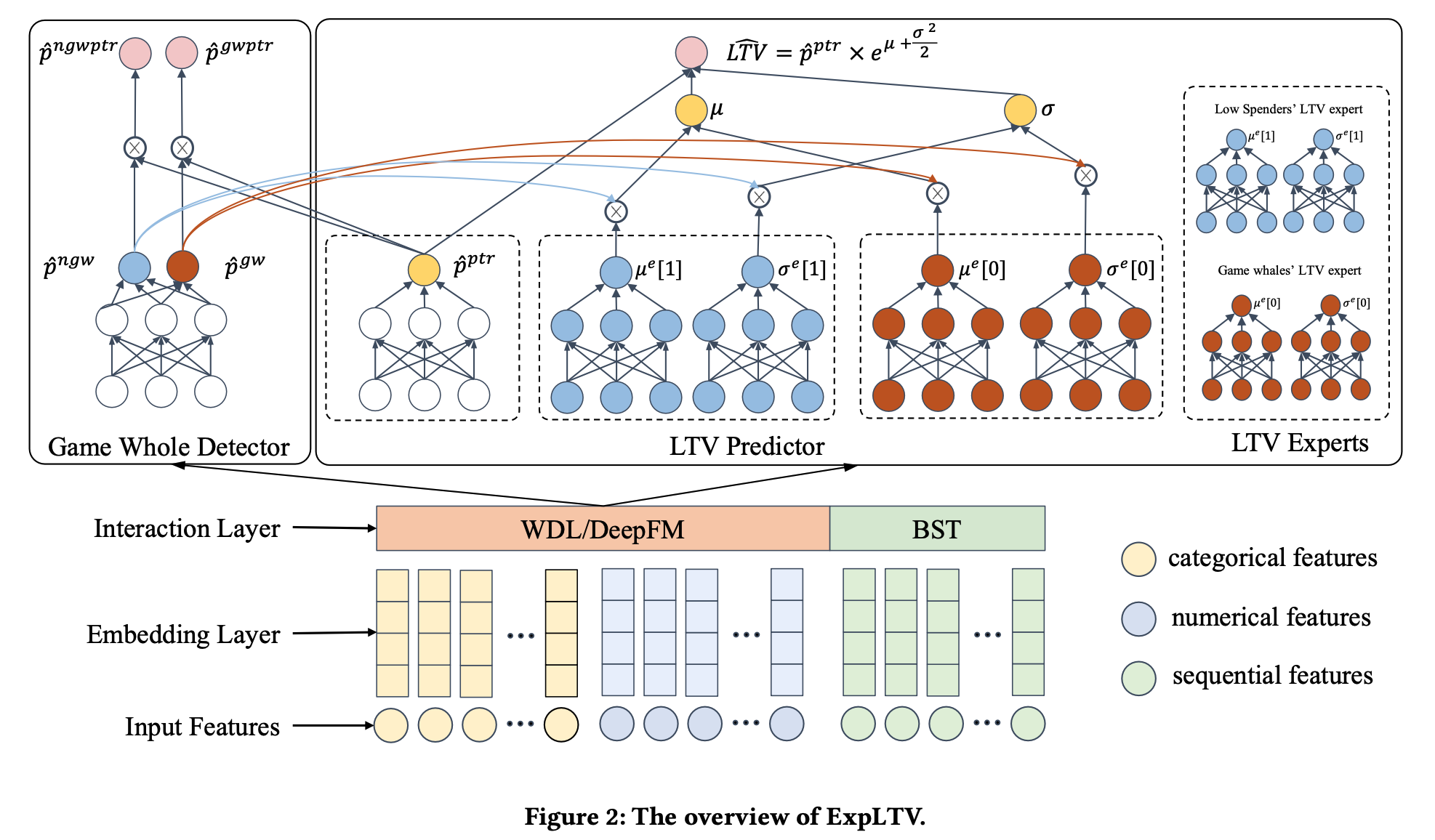
ExpLTV的模型架构如上图所示,下半部分是比较常规的特征处理以及用户序列建模的部分,重点关注上半部分,上半部分分为左右两个部分
- 左半部分建模游戏鲸鱼用户的购买概率和普通用户的购买概率
- 右半部分建模用户的LTV
鲸鱼用户/普通用户购买概率预估
由前面的定义可以得到鲸鱼用户和普通用户的购买概率可以拆解为用户是否是鲸鱼用户和用户的购买概率预估两个任务来表示:
\[ \hat{p}_{u}^{gwptr} = \hat{p}_{u}^{ptr} \times \hat{p}_{u}^{gw} \]
\[ \hat{p}_{u}^{ngwptr} = (1 - \hat{p}_{u}^{ptr}) + \hat{p}_{u}^{ptr} \times \hat{p}_{u}^{ngw} \]
拆解为两个任务而不直接预估用户是否是游戏鲸鱼用户的优点是,在真实数据中,只有0.7%的用户是游戏鲸鱼用户,但是有11%的用户会发生购买行为,联合建模可以缓解数据稀疏性问题
损失函数包含两个部分:交叉熵损失建模用户购买概率,KL散度建模鲸鱼用户购买概率:
\[ \mathcal{L}_{GWD} = \sum_{u \in \mathcal{D}} l_1(s_u, f_{ptr}(\mathbf{x}_u; \Theta_{ptr})) + D_{KL}(\mathbf{y} || \hat{\mathbf{y}}), \quad (10) \] 其中,\(\Theta_{ptr}\) 是估计器 \(f_{ptr}(\cdot)\) 的参数集,\(l_1(\cdot)\) 是交叉熵损失函数,\(\mathbf{y}\) 是 \(p_{u}^{gwptr}\) 和 \(p_{u}^{ngwptr}\) 的拼接。注意,根据定义 \(p_{u}^{ngwptr} = 1 - p_{u}^{gwptr}\) 。\(D_{KL}\) 是KL散度损失函数,它作为一种严格约束,用于缩小真实分布与GW检测器生成的结果分布之间的距离
LTV预估
LTV预估这部分采用了google ZILN 方法,不同点在于ExpLTV采用了两个专家网络来建模用户的LTV分布,并使用游戏鲸鱼检测网络预估的用户是游戏鲸鱼用户的概率作为权重来融合不同专家网络的预估结果,进而达到分人群建模的目的(鲸鱼用户和普通用户LTV分布不同)
\[ \begin{align*} \mu &= \hat{\mathbf{y}}_u \cdot \boldsymbol{\mu}^e = \hat{p}_u^{gw} \boldsymbol{\mu}^e[0] + \hat{p}_u^{ngw} \boldsymbol{\mu}^e[1] \\ \sigma &= \hat{\mathbf{y}}_u \cdot \boldsymbol{\sigma}^e = \hat{p}_u^{gw} \boldsymbol{\sigma}^e[0] + \hat{p}_u^{ngw} \boldsymbol{\sigma}^e[1], \end{align*} \]
loss函数和ZLIN完全相同:
\[ \mathcal{L}_{LTV} = l_1(\mathbb{I}_{s_u > 0}; p) + \left[ \mathbb{I}_{s_u > 0} \log(s_u \sigma \sqrt{2\pi}) + \frac{(\log s_u - \mu)^2}{2\sigma^2} \right] \]
最终训练时两个loss一起联合训练:
\[ \mathcal{L} = \mathcal{L}_{GWD} + \lambda \mathcal{L}_{LTV} \]
实验
评价指标
使用auc来评价ptr的准确性,使用归一化基尼系数来评价pltv准确性,使用topk召回率来评价游戏鲸鱼用户检测的准确性
实验结果

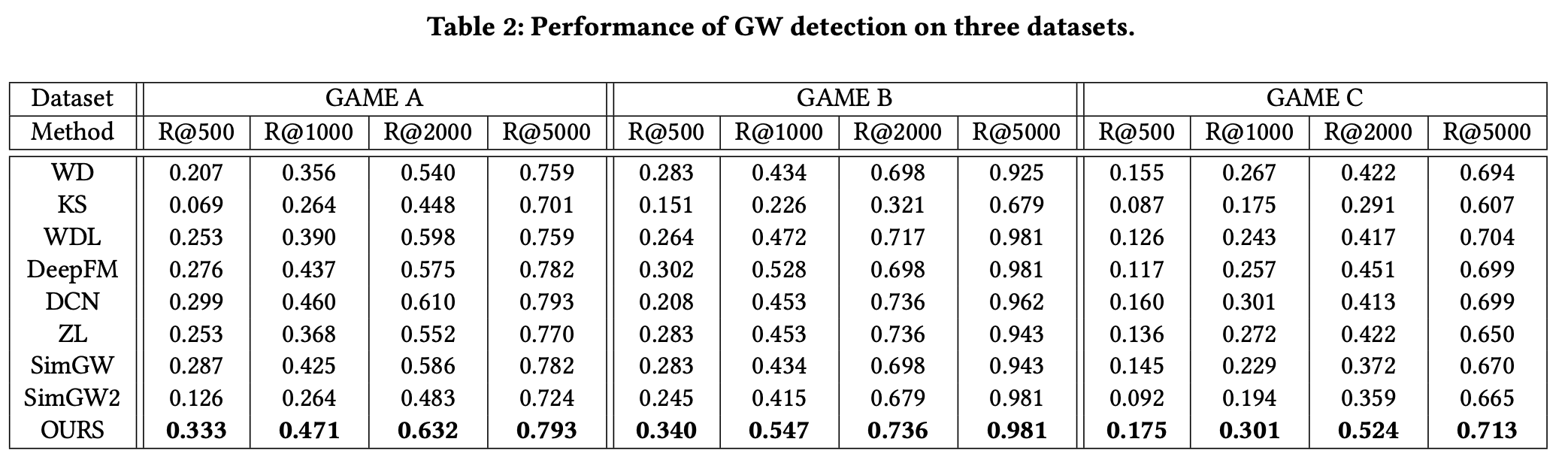




 浙公网安备 33010602011771号
浙公网安备 33010602011771号