google LTV预估论文《A Deep Probabilistic Model for Customer Lifetime Value Prediction》

问题

给定用户特征，预估未来n天的付费概率、付费金额

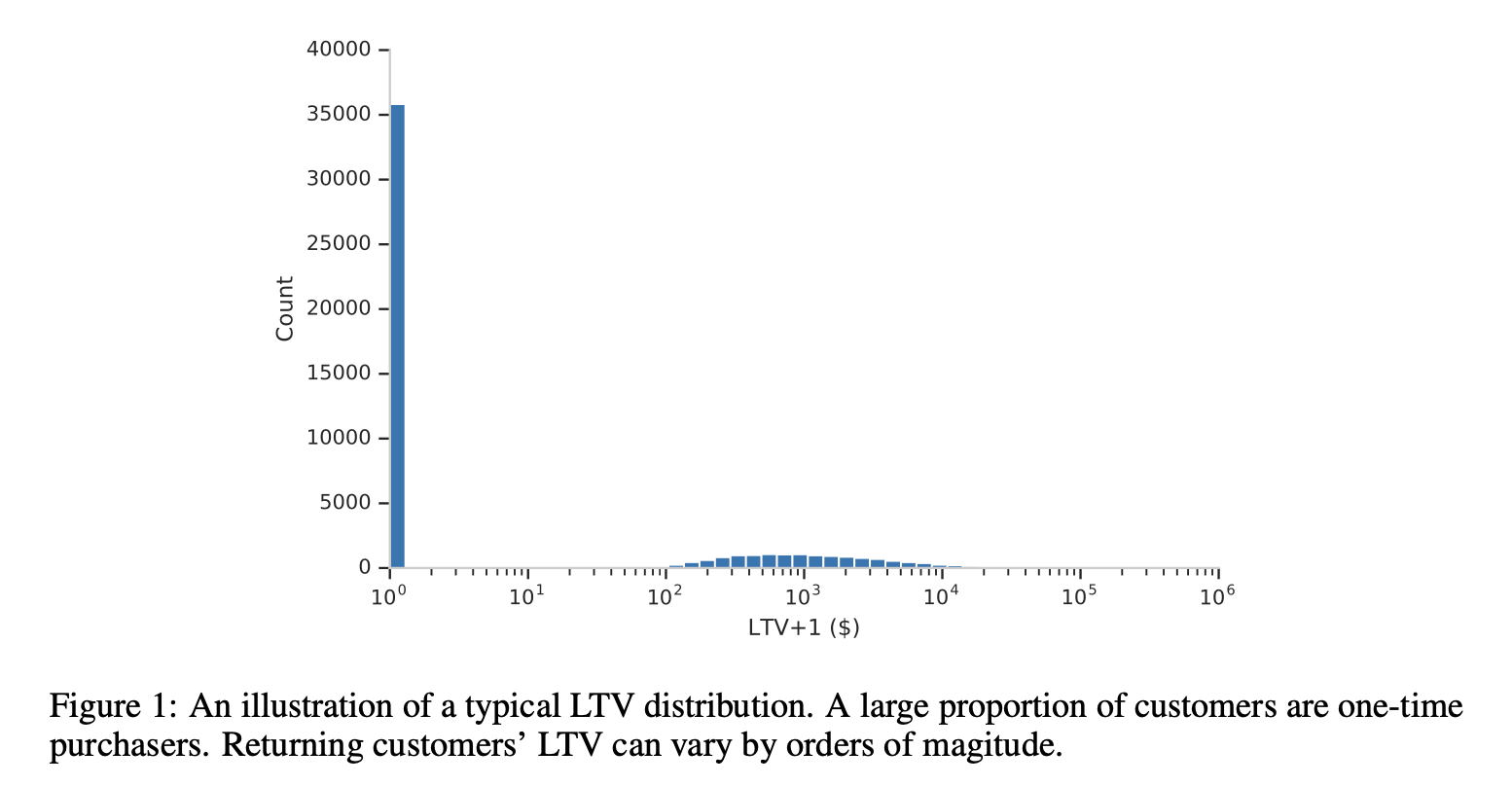
数据分布

长尾分布：90% 用户不付费，10% 用户付费
付费金额的范围非常广

建模方案

1. 直接用MSE建模LTV

缺点：由于用户LTR分布是0值和连续值的混合，而MSE假设label服从正态分布，容易被0值主导，模型倾向于预估一个接近0的值

2. 两阶段建模，先用BCE建模付费概率，然后用MSE建模付费金额，排除LTV为0的样本的影响

\[ pred\_ltv(x) = pay\_prob(x) \cdot pay\_amount(x) \]

缺点：需要两个模型，复杂度高，MSE对异常值太敏感，容易训崩

3. ZILN混合损失

本文提出了ZILN混合损失来同时建模用户是否付费以及付费金额：

\[ L_{\text{ZILN}}(x;p, \mu, \sigma) = L_{\text{CrossEntropy}}(\mathbb{1}_{\{x > 0\}};p) + \mathbb{1}_{\{x > 0\}}L_{\text{Lognormal}}(x;\mu, \sigma) \]

第一项用交叉熵来建模用户是否付费
第二项用对数正态分布建模LTV（假设了用户在已知付费的前提下付费金额服从对数正态分布），其中 x 为label，均值 μ 和方差 σ 为模型的输出值，线上infer时预估输出为学到的分布的期望 $exp(\mu + \sigma^{2}/2)$（是否需要乘以付费概率？）：\[ L_{\text{Lognormal}}(x;\mu, \sigma) = \log(x\sigma\sqrt{2\pi}) + \frac{(\log x - \mu)^2}{2\sigma^2} \]

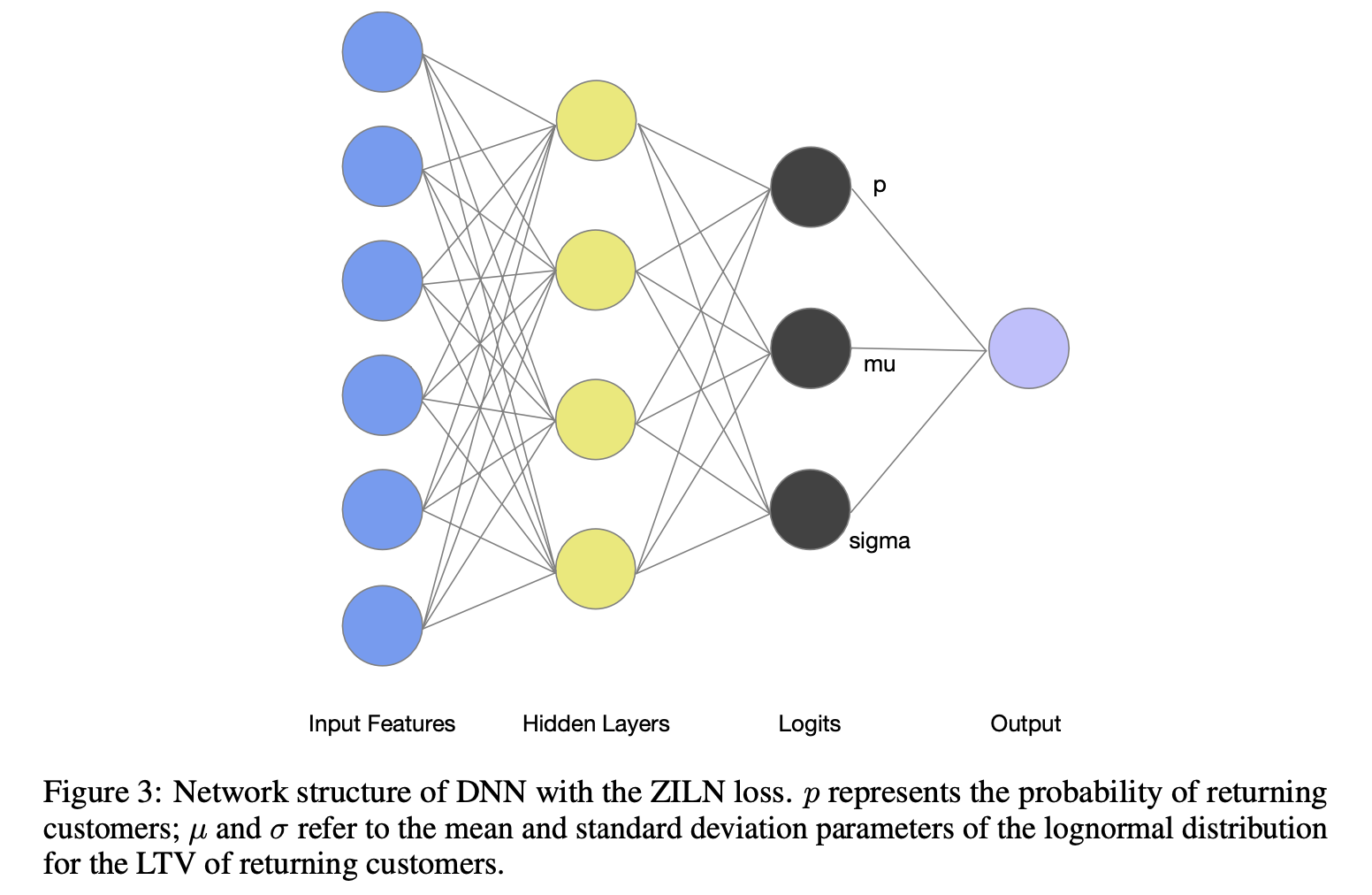
模型结构

模型结构入下图所示，DNN的最后一层保护3个输出，分别表示付费概率、均值 μ 和方差 σ（分别使用sigmoid、identity、softplus激活函数）

模型校准

按预测值从小到大排序，然后分桶校准：

\[ \text{MAPE} = \sum_{i = 1}^{10} \frac{|\hat{y}_i - y_i|}{y_i} \]

评价指标

使用AUC评估分类模型，使用基尼系数（对于任何二分类问题，基尼系数等于 2 倍的 AUC 减去 1）评估回归模型

基尼系数

基尼系数（Gini Coefficient）是衡量一个国家或地区居民收入分配公平程度的重要指标，由意大利统计学家科拉多・基尼（Corrado Gini）在 1912 年提出。它通过数值化的方式直观反映收入分配的不平等程度，是经济学中分析贫富差距的核心工具之一。

核心定义与取值范围

基尼系数的取值范围在 0 到 1 之间：

0：表示收入分配完全平等（所有人收入相同）。
1：表示收入分配完全不平等（全部收入集中在一人手中）。

数值越接近 0，说明收入分配越公平；越接近 1，则收入分配越悬殊。

计算原理

基尼系数的计算基于洛伦兹曲线（Lorenz Curve），其核心逻辑是通过曲线与绝对平等线的偏离程度来衡量不平等：

洛伦兹曲线：以人口累计百分比为横轴（如最贫困的 10% 人口、20% 人口等），以收入累计百分比为纵轴绘制的曲线。
绝对平等线：是一条从原点出发的 45° 直线，表示 “人口累计百分比 = 收入累计百分比”（如 20% 人口拥有 20% 收入）。
基尼系数公式： $$G = \frac{A}{A + B}$ 其中，A 是洛伦兹曲线与绝对平等线之间的面积（表示不平等程度），B 是洛伦兹曲线下方的面积。当 $A=0$ 时，$G=0$（完全平等）；当 $B=0$ 时，$G=1$（完全不平等）。$

论文中基尼系数计算方式：

按真实终身价值（LTV）降序排列（请注意，最初的定义是升序排列，我们将其改为降序，以便更直观地解读高价值客户）。
绘制洛伦兹曲线（加斯特沃思，1972 年），该曲线显示了总终身价值的累计百分比（纵轴）与客户累计百分比（横轴）的关系。曲线上的点（x, y）表示前 x% 的客户占据了总客户价值的 y%。当（x, y） = （20, 80）时，就变成了著名的 80/20 法则（特鲁斯韦尔，1969 年），也称为帕累托法则。
基尼系数是洛伦兹曲线与 45 度对角线之间面积的两倍，45 度对角线对应于客户的随机排序。它反映了客户消费的不平等程度，该值越大，分布的不平等程度就越高。

用模型预估LTV计算出来的是模型基尼系数，用真实LTV label计算出来的是标签基尼系数，用模型基尼系数除以标签基尼系数可以得到归一化基尼系数