回归任务常用损失函数及评价指标

损失函数

1. MSE（均方误差损失）

\[ C = (y - f(x))^2 \]

\[ \frac{\partial C}{\partial f(x)} = -2(y - f(x)) \]

优点：

1. 收敛快

缺点：

1. 假设了样本服从正态分布，如果训练样本label不服从正态分布，则MSE并非最大似然估计

2. 对异常点很敏感

 

2. MAE（平均绝对误差损失）

 \[ C = |y - f(x)| \] \[ \frac{\partial C}{\partial f(x)}= \begin{cases} -1, & \text{if } y > f(x) \\ 1, & \text{if } y < f(x) \end{cases} \]

优点：不容易受异常值影响

缺点：收敛速度慢，拟合能力弱

 

3. Huber Loss

\[ L_{\delta}(y, f(x)) = \begin{cases} \frac{1}{2}(y - f(x))^2, & \text{if } |y - f(x)| \leq \delta \\ \delta|y - f(x)| - \frac{1}{2}\delta^2, & \text{if } |y - f(x)| > \delta \end{cases} \] 

优点：结合了MSE和MAE的优点

缺点：需要调参

 

4. WCE

\[ C = - \sum_{i = 1}^{n} (y_i \log f(x_i) + \log(1 - f(x_i))), \text{ where } f(x) = \frac{1}{1 + e^{-\theta x}} \] 令\(y_i' = e^{\theta x_i}\) \[ C = - \sum_{i = 1}^{n} \left( y_i \log y_i' - (1 + y_i) \log(1 + y_i) \right) \] \[ \frac{\partial C}{\partial y_i'} = \frac{y_i' - y_i}{y_i'(1 + y_i')} \]

优点：把回归任务转化成了更容易学习的二分类任务

缺点：

1. wce loss在低估（y^'<y）和高估（y^'>y）时梯度不对称，低估时梯度很大，高估时梯度很小，很容易导致模型高估

2. 假设了样本分布服从几何分布，如果样本分布不是几何分布，可能导致效果不好

 

5. softmax+logloss

训练阶段：对label分桶，把回归问题转为多分类问题

serving阶段：落在每个桶的概率*桶均值（中位数）

优点：避免了原始回归问题对样本概率分布的先验假设，可以拟合任意概率分布

缺点：

1. 需要合理的对label分桶

2. 分桶方式太hard，连续桶交接处的loss变化过大

 

6. Ordinal Regression

参考论文《Deep Ordinal Regression Network for Monocular Depth Estimation》

 

7. Tweedie

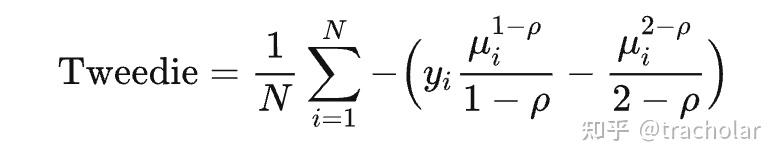
假设分布服从泊松-伽马分布 

https://zhuanlan.zhihu.com/p/629883594

 

参考资料

推荐系统中的回归建模