Weighted LR （WCE Weighted cross entropy）

背景

在推荐系统中，我们常常需要用用户的观看时长作为目标来进行建模，那么如何训练一个模型来预估模型的用户的播放时长呢？

很容易想到把播放时长的预估问题作为一个回归问题，采用mse loss，但是mse loss存在两个问题：

1. 分布假设：假设是预估label、误差项符合正态分布
2. 预估局限：对离群值敏感

 

loss 推导

Youtube在经典论文 (Deep Neural Networks for YouTube Recommendations) 提出了WCE损失函数，巧妙的用一个分类任务来预测播放时长

我们知道LR的对数几率可以表示为：

\[ \log \frac{P(Y = 1|x)}{1 - P(Y = 1|x)} = w \cdot x \]

正好就是模型过sigmoid函数之前的值，Youtube在论文中中指出可以把正样本的label置为t_i（观看时长），负样本的label为0，这样损失函数可以写为：

 \[ C = - \sum_{i = 1}^{n} (t_i y_i \log f(x_i) + (1 - y_i) \log(1 - f(x_i))), \text{ where } f(x) = \frac{1}{1 + e^{-\theta x}} \]

做如下推导：

\[ \frac{f(x)}{1 - f(x)} = e^{wx} = \frac{\sum_{i = 1}^{k} t_i}{n - k} \approx E(t) \]

 其中n是正样本的数目，k是负样本的数目，得出可以用 e^wx 来表示预估的观看时长

可以为每一个正例增加一个负例来解决近似的问题，用y表示时长，loss变为：

\[ C = - \sum_{i = 1}^{n} (y_i \log f(x_i) + \log(1 - f(x_i))), \text{ where } f(x) = \frac{1}{1 + e^{-\theta x}} \] 令\(y_i' = e^{\theta x_i}\) \[ C = - \sum_{i = 1}^{n} \left( y_i \log y_i' - (1 + y_i) \log(1 + y_i) \right) \] \[ \frac{\partial C}{\partial y_i'} = \frac{y_i' - y_i}{y_i'(1 + y_i')} \]

 可以得出wce loss在低估（y^'<y）和高估（y^'>y）时梯度不是对称的，低估时梯度很大，高估时梯度很小，很容易导致模型高估

WCE其实假设了样本分布服从几何分布，如果样本分布不是几何分布，可能导致效果不好

 

训练和serving

 

 

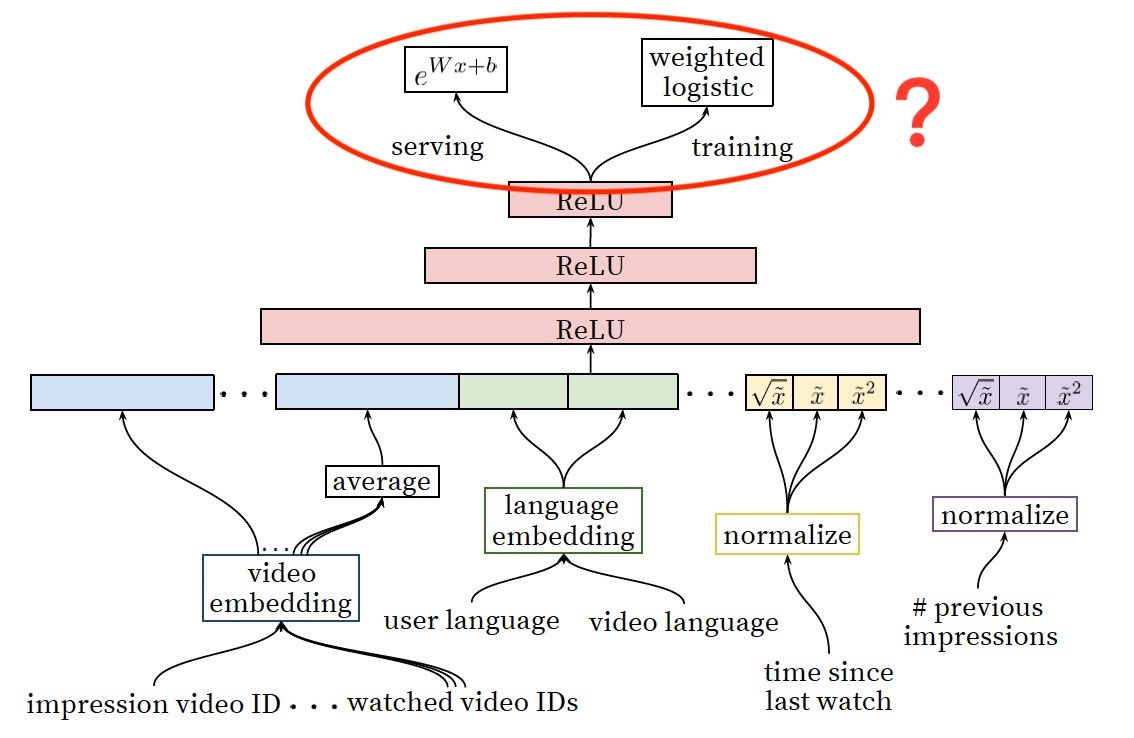
可以看到，训练时，还是当成一个二分类问题来训练就可以了

serving时，计算e^wx就是观看时长的预估值，完美的把一个回归任务转换成了一个分类任务

 

参考资料

https://zhuanlan.zhihu.com/p/61827629

https://www.cnblogs.com/hellojamest/p/11871108.html