阿里多兴趣序列建模论文MIND
背景
现在大部分召回模型都是把用户表示为一个embedding,但一个embedding很难捕获用户多方面的兴趣,MIND是阿里提出的用于召回阶段的多兴趣建模论文,这篇论文把用户表示成了多个兴趣向量
方法
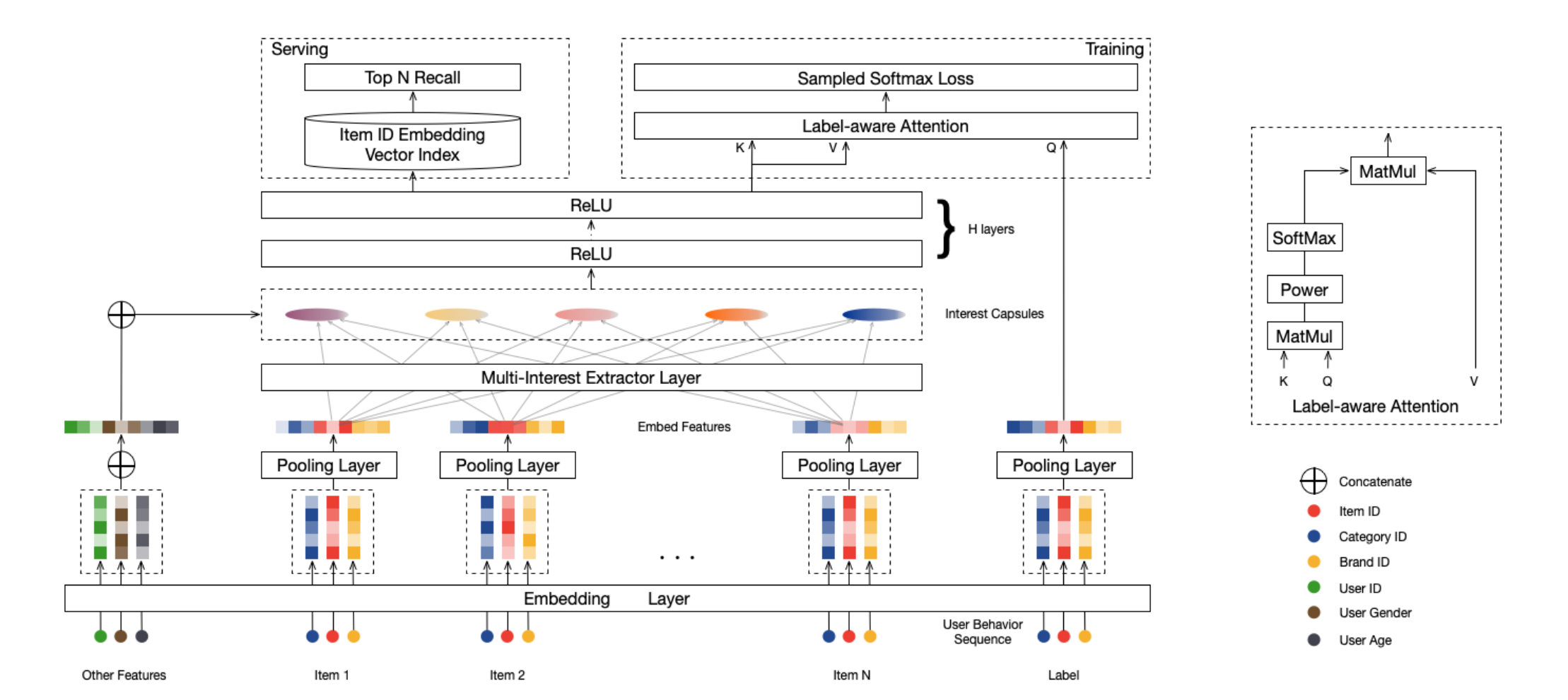
MIND的模型结构如上图所示,主要包含3个layer:
Embedding & Pooling Layer
该层的作用和普通的embedding层没有什么区别,都是把输入的特征转为embedding,输入的特征包含3类:用户画像$\mathcal{P}_u$、用户行为$\mathcal{I}_u$和候选item$\mathcal{F}_i$
Multi-Interest Extractor Layer
该层利用了胶囊网络从用户的行为序列里提取用户的多个兴趣向量,普通神经网络中的每个神经元都是一个标量,胶囊是一种由向量表示的新型神经单元。假设我们有两层胶囊,我们将第一层和第二层的胶囊分别称为低级胶囊和高级胶囊,我们的目的在于通过 Dynamic Routing(动态路由)的方式,根据low-level capsule来计算得到high-level的 capsule:
在每次迭代中,给定低级胶囊$\vec{c}_i^l \in \mathbb{R}^{N_l \times 1}, i \in \{1, \ldots, m\}$ ,其中$i \in \{1, \ldots, m\}$ ,以及高级胶囊$\vec{c}_j^h \in \mathbb{R}^{N_h \times 1}$,其中$j \in \{1, \ldots, n\}$ ,低级胶囊$i$与高级胶囊$j$之间的routing logit $b_{ij}$ 按如下方式计算:
\[ b_{ij} = (\vec{c}_j^h)^T S_{ij} \vec{c}_i^l \tag{4} \]
其中$S_{ij} \in \mathbb{R}^{N_h \times N_l}$ 表示待学习的双线性映射矩阵
计算出routing logit后,高级胶囊$j$的候选向量按所有低级胶囊的加权和来计算:
\[ \vec{z}_j^h = \sum_{i = 1}^{m} w_{ij} S_{ij} \vec{c}_i^l \tag{5} \]
其中$w_{ij}$ 表示连接低级胶囊$i$与高级胶囊$j$的权重,通过对routing logit执行softmax来计算:
\[ w_{ij} = \frac{\exp b_{ij}}{\sum_{k = 1}^{m} \exp b_{ik}} \tag{6} \]
最后,应用一个非线性“压缩”函数来得到高级胶囊的向量:
\[ \vec{c}_j^h = \text{squash}(\vec{z}_j^h) = \frac{\|\vec{z}_j^h\|^2}{1 + \|\vec{z}_j^h\|^2} \frac{\vec{z}_j^h}{\|\vec{z}_j^h\|} \tag{7} \]
$b_{ij}$ 的值初始化为零,路由过程通常重复迭代三次以上达到收敛。路由过程结束后,高级胶囊的值 $\vec{c}_j^h$ 固定下来,可作为下一层的输入
问题:胶囊网络相比用kmeans或多头attention提取多个用户兴趣的优点是什么?
论文对经典的capsule network作了一些调整,称为Behavior-to-Interest (B2I) dynamic routing,可以从字面意思理解,就是通过用户的行为,通过动态路由的方法得到用户兴趣向量。在这个场景下,low-level capsule对应用户的行为序列,high-level capsule对应用户的多个兴趣capsule。主要包含了以下三个方面的调整:
1. Shared bilinear mapping matrix
整个胶囊网络共享映射矩阵S,这样做有两个好处:
- 提升模型的泛化性
- 把用户不同的兴趣胶囊映射到同一个向量空间
2. Randomly initialized routing logits
由于使用了共享双线性映射矩阵$S$ ,将路由对数概率初始化为零会导致初始兴趣胶囊相同。这样一来,后续的迭代将陷入一种不同兴趣胶囊始终保持一致的情况。为缓解这一现象,我们从高斯分布$\mathcal{N}(0, \sigma^{2})$ 中采样一个随机矩阵来初始化路由对数概率,从而使初始兴趣胶囊彼此不同。
3. Dynamic interest number
根据用户行为序列长度不同,设置不通的兴趣胶囊数目,这样做的好处可以降低模型的学习难度,减少资源开销
\[ K'_u = \max(1, \min(K, \log_2(|\mathcal{I}_u|))) \]
完整的算法流程如下所示:

Label-aware Attention Layer
在上一步提取K个兴趣capsule之后,与用户基础属性embedding进行拼接,然后输入到H层relu全连接层网络,得到K个最终能够表征用户兴趣的向量Vu,在得到k个用户兴趣向量后,引入注意力机制,计算target item和k个用户向量的加权和:
\[ \vec{v}_u = \text{Attention}(\vec{e}_i, \text{V}_u, \text{V}_u) = \text{V}_u \text{softmax}(\text{pow}(\text{V}_u^T \vec{e}_i, p)) \]
其中p是一个超参数:
- 当p接近0时,则每个兴趣向量趋于相同的注意力权重
- 当p趋于无限大时,则会变成一种hard attention:只有最大注意力的兴趣向量起作用,而其他兴趣向量几乎被忽略,可以理解是每次只激活一个兴趣向量。
论文指出,采用hard attention可以更快收敛。
Training & Serving
Train
inbatch softmax训练:
\[ \mathrm{Pr}(i \mid u) = \mathrm{Pr}(\vec{e}_i \mid \vec{v}_u) = \frac{\exp(\vec{v}_u^{\mathrm{T}} \vec{e}_i)}{\sum_{j \in \mathcal{I}} \exp(\vec{v}_u^{\mathrm{T}} \vec{e}_j)} \]
\[ L = \sum_{(u, i) \in \mathcal{D}} \log \mathrm{Pr}(i \mid u) \]
Serving
1. 把用户特征过一遍Label-aware Attention Layer之前的网络,可以得到用户的多个兴趣向量
2. 用序列中的item embedding构建knn索引
3. 用每个用户兴趣向量进行knn检索,获取topk结果




 浙公网安备 33010602011771号
浙公网安备 33010602011771号