经典算法面试题
堆排序
10亿个数中取前1000大的数
维护一个1000个节点的小顶堆。
时间复杂度O(nlogk)
合并k个有序(假设升序)数组
具体步骤:(1)将k个数组的第一个元素取出来,维护一个小顶堆。
(2)弹出堆顶元素存入结果数组中,并把该元素所在数组的下一个元素取出来压入队中。
(3)调整堆的结构,使其满足小顶堆的定义。
(4)重复(2)(3)直到合并完成。

import heapq def fun(arrs): heap = [] for i in range(len(arrs)): if len(arrs[i]) > 0: heapq.heappush(heap, (arrs[i][0], i)) cur_pos = [0] * len(arrs) res = [] while heap: min_ele = heapq.heappop(heap) res.append(min_ele[0]) if len(arrs[min_ele[1]]) > cur_pos[min_ele[1]] + 1: cur_pos[min_ele[1]] += 1 heapq.heappush(heap, (arrs[min_ele[1]][cur_pos[min_ele[1]]], min_ele[1])) return res arrs = [[1], [3,3,5], [2,3,4,5,6,7]] print(fun(arrs))
归并排序
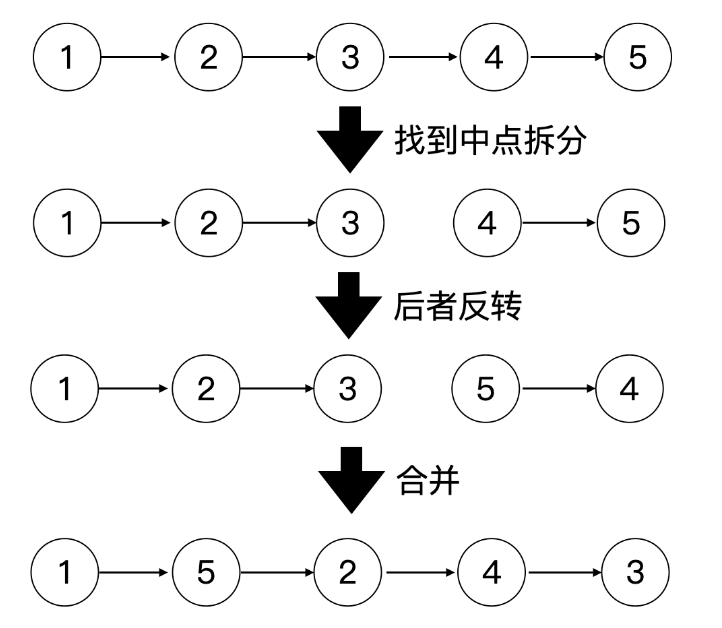
合并两个无序链表成一个有序链表,只能用常数空间。
归并排序的思想,用快慢指针不断二分链表。
快排
一个数组怎么输出前K大的值、时间复杂度
借助快排partition的思想,平均时间复杂度是O(n)
查找数组中出现次数超过一半的数字
等价于求数组中第n/2大的数,和4中思想一样,平均时间复杂度O(n)
动态规划
给定一个正整数 N,需要把它分解成至少两个不同的整数和,问有多少种不同的分解方案
动态规划:dp[n][m]表示n被分解为最大为m的数的方案数
\[dp\left[ n \right]\left[ m \right] = \sum\limits_{k = 1}^{m - 1} {dp\left[ {n - m} \right]\left[ k \right]} \]
二分
二维数组查找(剑指offer)
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
思路分析:我们注意到这个二维数组的行和列都是升序的,也就是说最上面的一行和最右边的一列在整体上也是升序的,在一个排序数组上查找某个我们会很自然的想起二分法。这样我们每次都把要查找的数和当前剩下的二维数组的右上角数字比较,这样每次我们都可以排除掉一行或一列。算法的时间复杂度是O(n+m),也就是行数加列数。
逆向遍历
题一:替换空格(剑指offer)
请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
题二:两个排序数组A1和A2,现在想把A2插入A1中并仍保持有序。
思路分析:数组是个顺序表,我们往数组中插入某个数的话必须要移动当前位置后面所有的数。常规的思路是每次插入一个数并移动后面的数,这样多次插入后会导致数组中有的数被移动了多次,极大浪费了效率。我们希望每个数移动一次就到达它最终的位置,所以我们往往会反向移动数组,这样做的好处是移动当前数时后面的数已经到达了最终位置,我们移动当前数不会影响到后面的数,这样就确保了每个数只被移动一次。
循环替代递归
斐波那契数列高效计算
斐波那契数列:f(0) = 0, f(1) = 1, f(n) = f(n - 1) + f(n - 2)
方法一:递归,效率低
方法二:循环,正着推
方法三:矩阵运算
进制转换
用A表示1第一列,B表示2第二列,。。。,Z表示26,AA表示27,AB表示28。。。以此类推。请写出一个函数,输入用字母表示的列号编码,输出它是第几列。
解题思路:26进制转10进制。
位运算
输出一个整数二进制表示中1的个数
解法1:右移原数判断,如果输入是负数可能陷入死循环。
解法2:左移1
解法3:把一个整数-1后与原数做与运算会消去原数最左边的1
一个数组中有2n + 1个数,其中只有一个数只出现一次,找出只出现一次的那个数
异或运算
一个数组中有2n + 2个数,其中只有两个个数只出现一次,找出只出现一次的那两个个数
1. 对原数组做异或运算得到的结果就是那两个只出现一次的数的异或结果
2. 找出前面的异或结果第一位为1的位置,在这个位置上这两个只出现一次的数必然一个是0一个是1
3. 按照这个这位置可以把原数组分为两个数组,一个数组所有数这个位置都为1,另一个数组所有数这个位置都为0
4. 对上面两个数组分别进行异或就可以得到最终的结果
链表
O(1)时间删除链表指定节点(给定单向链表的头指针和一个节点指针)
解题思路:把该节点下个节点的值复制到该节点,删除下个节点(注意该节点是尾节点和链表只有一个节点的特殊情况)
技巧题
最小方差划分
把一个数组划分成两部分,使其方差和最小。
D(X) = E(x^2) - [E(X)]^2
迭代求和。
树
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先

/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { if(root == NULL || root == p || root == q) return root; TreeNode *left = lowestCommonAncestor(root->left, p, q); TreeNode *right = lowestCommonAncestor(root->right, p, q); if(left != NULL && right != NULL) return root; return left==NULL? right: left; } };
队列和栈相互模拟
用两个栈模拟一个队列
压入:向stack1压入元素
弹出:如果stack2非空就从stack2弹出,否则就弹出stack1所有元素逐个压入stack2中,然后从stack2中弹出元素。
用两个队列模拟一个栈
压入:向queue1(queue2)压入元素
弹出:把queue1(queue2)元素逐个弹出并压入queue2(queue1)中直至最后一个元素,最后一个元素直接弹出
用两个栈模拟双端队列
前缀和
O(1)时间复杂度查询数组任意两个位置之间的元素和
解题思路:前缀和模版题,前序遍历计算每个位置的前缀和并保存为sums,查询时计算sums[j] - sums[i]即可获得结果

class NumArray: def __init__(self, nums: List[int]): self.sums = [0] * len(nums) self.sums[0] = nums[0] for i in range(1, len(nums)): self.sums[i] = self.sums[i-1] + nums[i] def sumRange(self, left: int, right: int) -> int: if left < 0 or right >= len(self.sums): return None if left == 0: return self.sums[right] else: return self.sums[right] - self.sums[left-1]
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
子数组是数组中元素的连续非空序列。
示例 1:
输入:nums = [1,1,1], k = 2 输出:2
示例 2:
输入:nums = [1,2,3], k = 3 输出:2
解题思路:遍历数组计算以当前位置结尾和为k的子数组数目
- 遍历数组计算前缀和
- 遍历数组,遍历过程中用hash表保存每个前缀和出现的数目,此时只要判断当前位置之前的前缀和为sum[i] - k数目就是以当前位置结尾和为k的子数组数目

class NumArray: def __init__(self, nums: List[int]): self.sums = [0] * len(nums) self.sums[0] = nums[0] for i in range(1, len(nums)): self.sums[i] = self.sums[i-1] + nums[i] def sumRange(self, left: int, right: int) -> int: if left < 0 or right >= len(self.sums): return None if left == 0: return self.sums[right] else: return self.sums[right] - self.sums[left-1] # Your NumArray object will be instantiated and called as such: # obj = NumArray(nums) # param_1 = obj.sumRange(left,right)
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
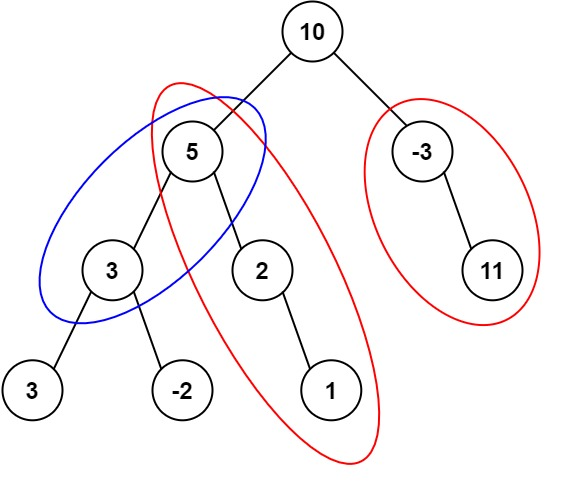
输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出:3 解释:和等于 8 的路径有 3 条,如图所示。
解题思路:437进阶版,dfs遍历数组,遍历过程中计算以前当前结点为终点的和为targetSum的路径数

# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int: res = 0 def dfs(root, k, hs, curr_sum): if root == None: return nonlocal res curr_sum += root.val if curr_sum == k: res += 1 res += hs[curr_sum - k] hs[curr_sum] += 1 dfs(root.left, k, hs, curr_sum) dfs(root.right, k, hs, curr_sum) hs[curr_sum] -= 1 hs = defaultdict(int) dfs(root, targetSum, hs, 0) return res
拓扑排序

解题思路:判断有向图中有没有环,依次遍历出度数为0的结点,删除该结点的同时更新父节点的出度数,最后遍历所有节点,如果有节点的出度数大于0则有环,否则无环

class Solution: def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool: nums = [0] * numCourses edges = defaultdict(list) for x in prerequisites: edges[x[1]].append(x[0]) nums[x[0]] += 1 from queue import Queue que = Queue() for i in range(len(nums)): if nums[i] == 0: que.put(i) while not que.empty(): p = que.get() for q in edges[p]: nums[q] -= 1 if nums[q] == 0: que.put(q) for x in nums: if x: return False return True
哈希
概率论
已知rand5函数可以等概率生成0~4之间的随机数,请实现rand7函数等概率生成0~6之间的随机数
解题思路:rand5 * 5 + rand5 可以等概率生成0~24之间的随机数
方法一:重复多次,直到生成0~6之间的随机数
方法二:重复多次,自到生成0~20之间的随机数,并把结果整除3
给定一个数组 [1,5,2,3,5,5,3],以均匀的概率返回最大值所在的索引,要求只遍历一次,并且空间复杂度为O(1)
方法1:遍历两次,第一次遍历统计最大值个数,然后生成 [0, 最大值个数) 之间的随机数,根据随机数结果就可以知道当前需要取第几个最大值的位置索引了,遍历一次即可
方法2:
- 遍历到第一个最大值位置时,记录最大值为当前位置索引
- 遍历到第二个最大值位置时,记录最大值为当前位置索引为1/2
- 遍历到第三个最大值位置时,记录最大值为当前位置索引为1/3
- 以此类推





 浙公网安备 33010602011771号
浙公网安备 33010602011771号