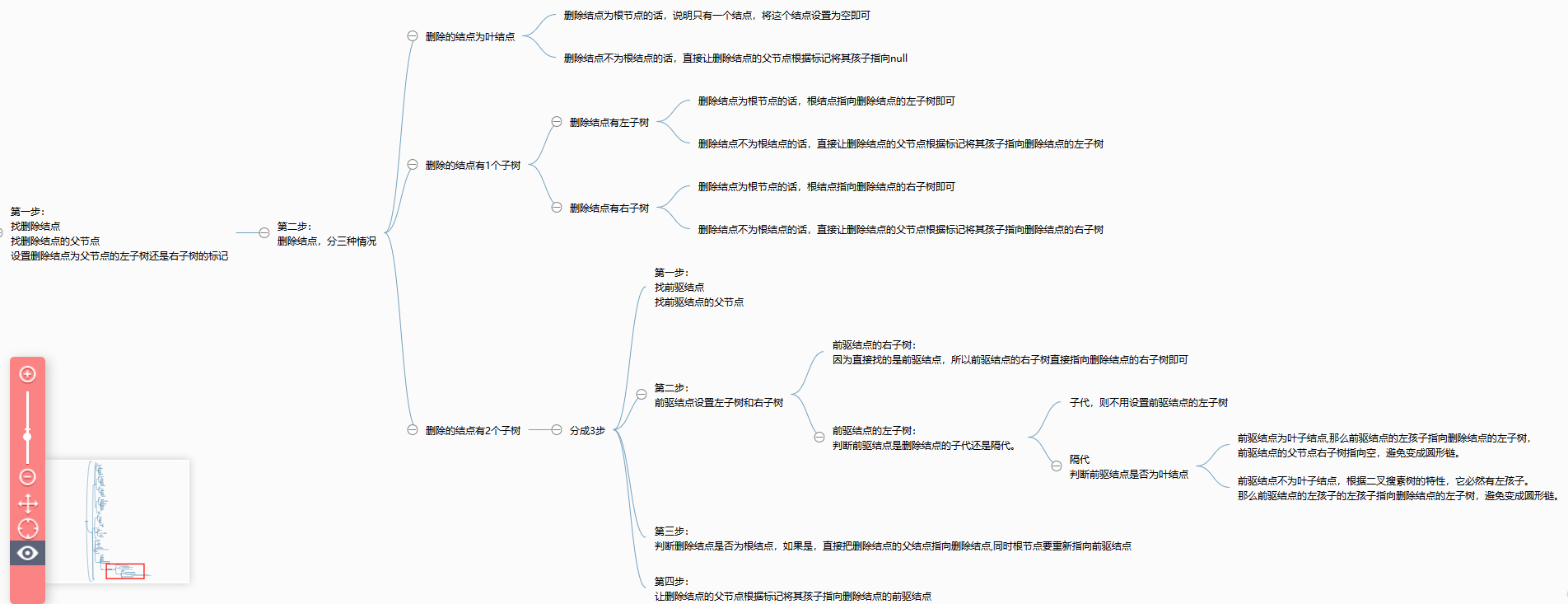
二叉搜索树最麻烦的地方就是删除结点了,具体步骤如图。
function BinarySearchTree() {
// 定义BST实例的属性
this.root = null;
this.count = 0;
// 定义构造结点的函数
function Node(key) {
this.key = key;
this.left = null;
this.right = null;
}
// 插入
BinarySearchTree.prototype.insert = function (key) {
var newNode = new Node(key);
if (this.root == null) {
this.root = newNode;
}
else {
insertNode(this.root, newNode);
}
this.count++;
// 递归插入
function insertNode(node, newNode) {
// 向左递归
if (node.key > newNode.key) {
if (node.left == null) {
node.left = newNode;
}
else {
insertNode(node.left, newNode);
}
}
// 向右递归
else {
if (node.right == null) {
node.right = newNode;
}
else {
insertNode(node.right, newNode);
}
}
}
}
// 前序遍历
BinarySearchTree.prototype.preOrderTraverse = function () {
var str = "";
pre(this.root)
// 递归
function pre(node) {
if (node == null) {
return;
}
else {
str += node.key + " " // 根
pre(node.left); // 左
pre(node.right); // 右
}
}
console.log(str);
}
// 中序遍历
BinarySearchTree.prototype.midOrderTraverse = function () {
var str = "";
mid(this.root)
// 递归
function mid(node) {
if (node == null) {
return;
}
else {
mid(node.left); // 左
str += node.key + " " // 根
mid(node.right); // 右
}
}
console.log(str);
}
// 后序遍历
BinarySearchTree.prototype.postOrderTraverse = function () {
var str = "";
post(this.root)
// 递归
function post(node) {
if (node == null) {
return;
}
else {
post(node.left); // 左
post(node.right); // 右
str += node.key + " " // 根
}
}
console.log(str);
}
// 最小值
BinarySearchTree.prototype.getMin = function () {
return left(this.root);
// 利用二叉搜索树的特性,进行递归查找左结点即为最小值
function left(node) {
var key;
if (node == null) {
return key;
}
else if(node.left = null) {
key = left(node.left);
}
else {
key = node.key;
}
return key;
}
}
// 最大值
BinarySearchTree.prototype.getMax = function () {
return right(this.root);
// 利用二叉搜索树的特性,进行递归查找右结点即为最大值
function right(node) {
var key;
if(node == null) {
}
else if(node.right != null) {
key = right(node.right);
}
else {
key = node.key;
}
return key;
}
}
// 根据key查找结点, 返回node,找不到则返回undefined;
BinarySearchTree.prototype.search = function(key) {
return search(this.root,key);
// 利用二叉搜索树的特性,进行递归查找
function search(node,key) {
var result ;
if(node === null) {
}
else if(node.key == key){
result = node;
}
else {
// 向左查找
if(key < node.key ) {
result = search(node.left,key);
}
// 向右查找
else {
result = search(node.right,key);
}
}
return result;
}
}
BinarySearchTree.prototype.reMove = function(key) {
//第一步:找到要删除的结点,其中要保留父节点,当前结点,以及标记该结点是父结点的左子还是右子结点。
var parentNode = null; //保留父节点
var current = this.root; //当前结点
var isLeftChild = true; //标记删除结点是父结点的左子还是右子结点
while(current.key!=key && current != null) {
parentNode = current; //保留父节点
//判断往左 还是往右
if(current.key > key) {
current = current.left;
isLeftChild = true;
}
else {
current = current.right;
isLeftChild = false;
}
}
// 说明未找到。
if(current == null) return false;
console.log("当前结点:"+current.key)
//第二步:根据找到的结点 进行不同情况的删除。
// 1 叶节点的情况,我们只需要把叶节点设置成null即可
if(current.left == null && current.right == null) {
console.log("删除叶结点")
// 1.1该节点为根结点
if(current == this.root) {
this.root = null;
}
// 1.2该节点不为根结点
else{
isLeftChild ? parentNode.left=null:parentNode.right=null;
}
}
// 2 节点且只有一个子节点的情况 我们只需要把父节点指向子节点即可
// 2.1只有左子结点
else if (current.left != null && current.right == null) {
console.log("删除只有1个子结点的结点")
//判断是否为为根结点
if(current == this.root) {
this.root = current.left;
}
else {
isLeftChild ? parentNode.left = current.left : parentNode.right = current.left;
}
}
// 2.2只有右子结点
else if(current.left == null && current.right != null) {
console.log("删除只有1个子结点的结点")
//判断是否为为根结点
if(current == this.root) {
this.root = current.right;
}
else {
isLeftChild ? parentNode.left = current.right : parentNode.right = current.right;
}
}
// 3 有2个子节点的情况 我们要根据替换的规律 既是在左子树中找最大的值(前驱) 或者 在右子树中找最小的值(后继) 然后与该结点替换。再将给结点设置为null
else {
console.log("删除有2个子结点的结点")
// 3.2.1定义前驱结点,前驱结点的父结点
var frontNode = current.left; // 前驱结点
var frontParentNode = current; // 前驱结点的父结点
// 3.2.2循环找前驱结点,前驱结点的父结点
while(frontNode.right!=null) {
frontParentNode = frontNode;
frontNode = frontNode.right;
}
console.log("前驱结点"+frontNode.key,"前驱结点的父结点"+frontParentNode.key);
// 3.2.3开始删除结点
// 3.2.3.1因为直接找的是前驱结点,所以前驱结点的右孩子直接指向删除结点的右孩子即可。
frontNode.right = current.right;
// 3.2.3.2判断前驱结点是删除结点的子代还是隔代。
// 如果是隔代 在考虑两种情况下把删除结点的左子树赋值给前驱结点。
if(frontParentNode != current ) {
//第一种情况,如果前驱结点为叶子结点,那么前驱结点的左孩子指向删除结点的左子树,前驱结点的父节点右子树指向空,避免变成圆形链。
if(frontNode.left == null) {
frontNode.left = current.left;
frontParentNode.right = null;
}
//第二种情况,如果前驱结点不为叶子结点,根据二叉搜素树的特性,它必然有左孩子。那么前驱结点的左孩子的左孩子指向删除结点的左子树,避免变成圆形链。
else {
frontNode.left.left = current.left;
frontParentNode.right = null;
}
}
// 3.3 判断删除结点是否为根结点,如果是,直接把删除结点的父结点指向删除结点,同时根节点要重新指向前驱结点。
if(current == this.root) {
parentNode = current;
this.root = frontNode;
}
// 3.4删除结点
isLeftChild ? parentNode.left = frontNode : parentNode.right = frontNode;
}
}
}
var bst = new BinarySearchTree();
bst.insert(11);
bst.preOrderTraverse();
bst.midOrderTraverse();
bst.postOrderTraverse();
bst.reMove(11)
bst.preOrderTraverse();




 浙公网安备 33010602011771号
浙公网安备 33010602011771号