上下界网络流

https://zhuanlan.zhihu.com/p/324507636

考虑在满足边上下界的限制下满足流量平衡。

那么先流满下界网络，然后随便流差网络，那么对于原图的一个流就是 2 者相加。但是不一定合法，因为不一定满足流量平衡。

我们考虑从需要流满的下界网络入手。

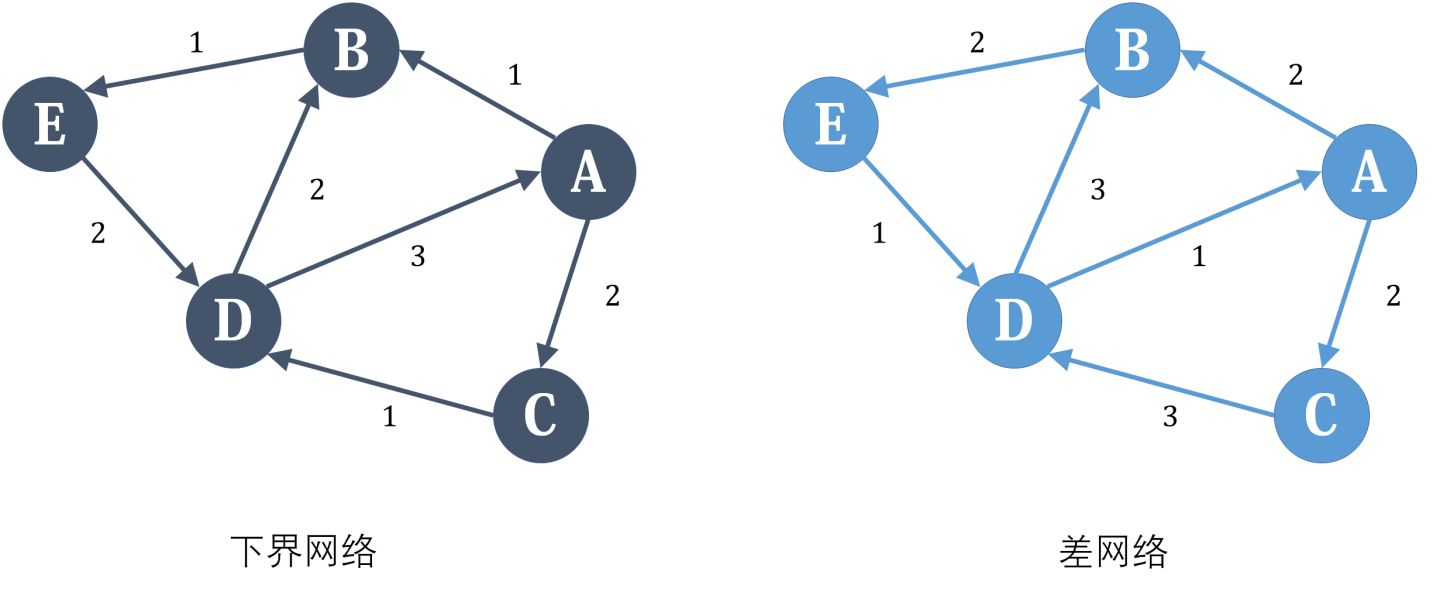
需要明确的是，我们现在只有 1 个目标。让差网络的流加上下界网络的满流后使得流量平衡。

网络流只能解决给定上界，然后流量平衡。但是我们可以判是否流满上界。

我们分别考虑下界网络的每个点。A点，流入量为3，流出量也为3，所以是平衡的，那么在差网络中，也应该是平衡的，所以不做修改。B点，流入量为3，流出量为1，流入比流出多2，所以我们希望在差网络中，B的流出应该比流入多2，但是对于原先差网络的流是一定满足流入等于流出的。那么这流出多出来的 2 是不是需要别的地方流来，流出就还是需要经过原先差网络。又因为源汇可以不满足流量平衡，所以就从源点流来。于是我们在差网络中新设一个源点，然后加入一条容量为2的附加边从源点连向B，然后这附加边一定需要通过若干差网络中的边流满。

也就是说，当我们跑源点到汇点的流时，假如我们附加边都流满，又因为下界网络默认流满了，那是不是一定满足流量平衡。

有源汇只要考虑我们无源汇解决的是每个点都满足流量平衡。

但是有源汇的 \(s,t\) 本身就满足 \(s\) 的流出等于 \(t\) 的流入，假如你从 \(s\) 开始跑的话，于是，你要让 \(s\) 的流入等于 \(s\) 的流出 等于 \(t\) 的流入等于 \(t\) 的流出。

为了流量平衡，我们可以将 \(t\) 的流入再流回 \(s\)，即建 \(t\to s\) 上界为 \(\infty\) 的边，然后就是无源汇了。

考虑有源汇最大流。

通过差网络流满了附加边，那么还能浮动的是不是差网络非附加边的剩余流量。那么只要再跑一遍最大流即可。

https://loj.ac/p/115

板子 loj 有。

有时候好像要加负环费用流来着。

https://www.luogu.com.cn/problem/P7173