Strassen算法
问题
n×n的两个方阵a和b相乘,简单考虑,复杂度为O(n^3)。Strassen算法给出了优化。
例子
将n×n矩阵划分为子矩阵后再相乘
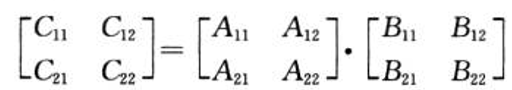
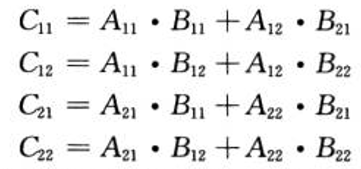
普通分治
采用递归划分矩阵直至子矩阵变为1×1

运行时间
令T(n)为两个n×n矩阵相乘时间
-
n=1
T(1) = Θ(1) -
n>1
- 分解矩阵
Θ(1) - 8次递归
8T(n/2) - 4次矩阵加法
Θ(n^2)
T(n)=Θ(1)+8T(n/2)+Θ(n^2)=8T(n/2)+Θ(n^2) - 分解矩阵
运行时间递归式
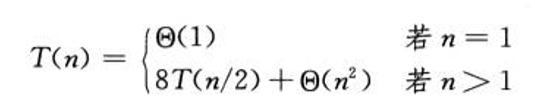
使用主方法求解递归式,得到T(n)=Θ(n^3)
Strassen算法
-
创建10个如下矩阵
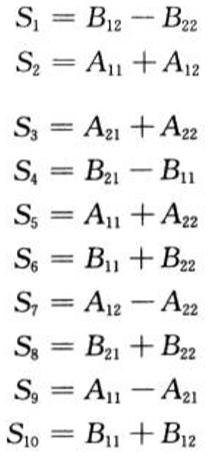
花费时间Θ(n^2) -
计算7次如下乘法
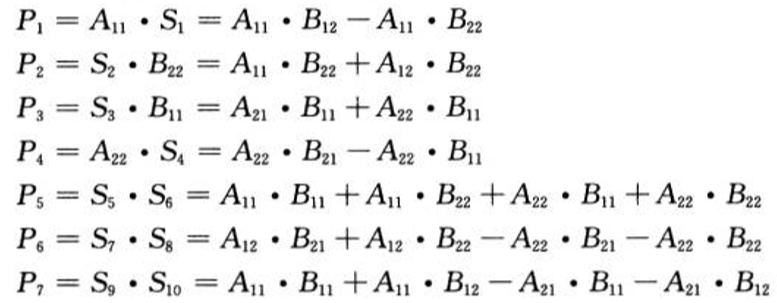
花费时间7T(n/2) -
计算C
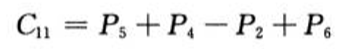
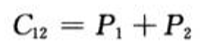

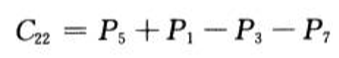
花费时间Θ(n^2)
运行时间递归式
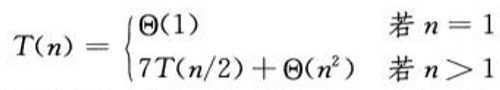
递归式的解为
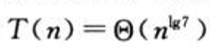


 缩短方阵相乘运行时间
缩短方阵相乘运行时间

 浙公网安备 33010602011771号
浙公网安备 33010602011771号