算法导论中函数增长的几种记法

Θ

f(n) = Θ(g(n))

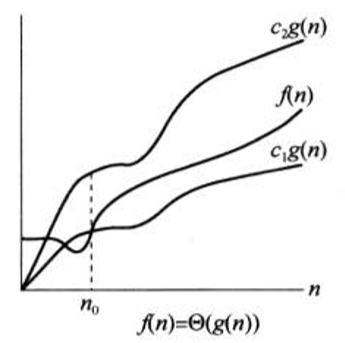
表示当n足够大时，存在正常数\(c_1\), \(c_2，使得\)c_2$g(n) < f(n) < \(c_1\)g(n)。使用g(n)划出了f(n)的上界和下界。

O

f(n) = O(g(n))

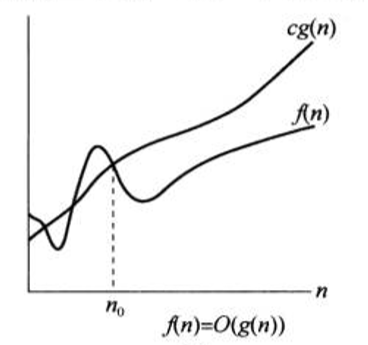
表示当n足够大时，存在正常数c，使得f(n) < cg(n)。使用g(n)划出了f(n)的上界。

Ω

f(n) = Ω(g(n))

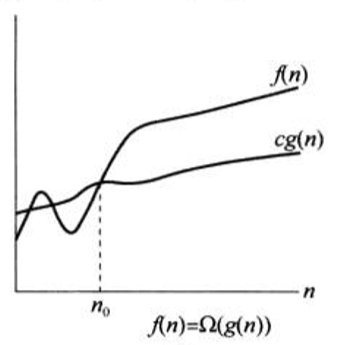
表示当n足够大时，存在正常数c，使得cg(n) < f(n) 。使用g(n)划出了f(n)的下界。

o

f(n) = o(g(n))

表示当n足够大时，任意正常数c都能使得f(n) < cg(n)，不如O记法精确。

ω

f(n) = ω(g(n))

表示当n足够大时，任意正常数c都能使得f(n) > cg(n)，不如O记法精确。