NOI Section 1 图论
NOI Section 1 图论
目录
- 最短路
- 生成树
- 拓扑排序
- 差分约束
- 传递闭包
- 联通分量(Tarjan)
- 二分图
- 次短路
最短路
P1821 [USACO07FEB] Cow Party S
problem
一张\((V,E)=(n,m)\)有向图,指定一个点\(x\),求所有点到这个点再返回的最短路径的最大值。其中,去程和返程都行走最短路径。
constraint
\(1≤x≤n≤10,1 \leq m \leq 10^5\)
solution
建反边。
一张图存正向行走,一张图存反向行走,最终距离之和最小即可。
code
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
const int maxn=1e6+10;
const int mod=1e9+7;
#define int long long
#define inf 0x3f3f3f3f3f
int read(){
int a=0,op=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') op=-1;c=getchar();}
while(c>='0'&&c<='9') a*=10,a+=c^48,c=getchar();
return a*op;
}
int cnt,head[maxn];
int cntnew,headnew[maxn];
struct node{
int to,nxt,val;
}e[maxn<<2],enew[maxn<<2];
void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].nxt=head[u];
e[cnt].val=w;
head[u]=cnt;
}
void addnew(int u,int v,int w){
enew[++cntnew].to=v;
enew[cntnew].nxt=headnew[u];
enew[cntnew].val=w;
headnew[u]=cntnew;
}
int n,m,st,x,y,z,curr,minn=inf,maxx=-inf;
int currnew;
bool vis[maxn]={0};
int dis[maxn];
bool visnew[maxn]={0};
int disnew[maxn];
signed main(){
n=read(),m=read(),st=read();
for(int i=1;i<=n;i++) dis[i]=inf,disnew[i]=inf;
for(int i=1;i<=m;i++){
x=read(),y=read(),z=read();
add(y,x,z);
addnew(x,y,z);
}
curr=st,dis[st]=0;
while(!vis[curr]){
vis[curr]=1;
for(int i=head[curr];i;i=e[i].nxt){
int p=e[i].to;
if(!vis[p]&&dis[p]>dis[curr]+e[i].val)
dis[p]=dis[curr]+e[i].val;
}
minn=inf;
for(int i=1;i<=n;i++)
if(!vis[i]&&minn>dis[i]) minn=dis[i],curr=i;
}
currnew=st,disnew[st]=0;
while(!visnew[currnew]){
visnew[currnew]=1;
for(int i=headnew[currnew];i;i=enew[i].nxt){
int p=enew[i].to;
if(!visnew[p]&&disnew[p]>disnew[currnew]+enew[i].val)
disnew[p]=disnew[currnew]+enew[i].val;
}
minn=inf;
for(int i=1;i<=n;i++)
if(!visnew[i]&&minn>disnew[i]) minn=disnew[i],currnew=i;
}
for(int i=1;i<=n;i++) maxx=max(dis[i]+disnew[i],maxx);
printf("%lld",maxx);
return 0;
}
P1875 佳佳的魔法药水
problem
共\(N\)种药水从\(0\)~\(N-1\)编号,每种药水有自己的固定价值。有\(m\)条规则,可以将一瓶\(a\)药水和一瓶\(b\)药水合并成一瓶\(c\)药水。为了获得一瓶\(0\)号药水,最少的花费是多少?有多少种达到最少花费的购买和合成方式?两种可行的配置方案如果有任何一个步骤不同则视为不同的。
constraint
\(N\le 1000\)。注意,某两种特定的药水搭配如果能配成新药水的话,那么结果是唯一的。也就是 说不会出现某两行的\(a,b\)相同但\(c\) 不同的情况。
solution
djikstra一个很重要的特征是每当我要从一个点出发,更新其他点的最短路径时,这个点必须已经确定了最短路径的值,不会再改了,即vis[i]=1,而当前队列中已知距离起点最近的点一定是已经确定了最短路径的点,因为已经不可能有某种再拐一下的方法使该距离更近了。(这玩意在我刚学djikstra的时候困扰了我好久其实也就是昨天)。
但对于这道题我们发现,当我们走的时候,我们要从两个起点出发,而非一个。我们已经知道,djikstra要求我们必须从已确定最短路径的点出发,那么对于两个起点该怎么办呢?很简单,只要等两个起点都是已知最短路径不就行了
在更新之前,我们判断一下另一个需要的药水是否已知最低消费即可。不用担心这样会不会漏掉配方,反正我们的前向星是存了两遍的。
code
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
using namespace std;
const int maxn=1e6+10;
const int mod=1e9+7;
#define int long long
#define inf 0x3f3f3f3f3f
int read(){
int a=0,op=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') op=-1;c=getchar();}
while(c>='0'&&c<='9') a*=10,a+=c^48,c=getchar();
return a*op;
}
int cnt,head[maxn];
struct node{
int to,nxt,val;
}e[maxn<<2];
void add(int u,int v,int w){
e[++cnt].to=v,e[cnt].val=w,e[cnt].nxt=head[u],head[u]=cnt;
}
struct node2{
int cost,ans;
bool v;
}ptn[maxn];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q;
int n,val[maxn],curr,minn=inf,maxx=-inf,a,b,c;
int num[maxn],dis[maxn];
bool vis[maxn]={0};
signed main(){
n=read();
for(int i=0;i<n;i++)
ptn[i].cost=read(),ptn[i].ans=1,q.push(make_pair(ptn[i].cost,i));
while(scanf("%lld %lld %lld",&a,&b,&c)!=EOF){
add(a,b,c);
if(a==b) continue;add(b,a,c);
}
while(!q.empty()){
int c=q.top().first,u=q.top().second;
q.pop();
if(c!=ptn[u].cost) continue;
ptn[u].v=1;
for(int i=head[u];i;i=e[i].nxt){
int x=e[i].to,v=e[i].val;
if(ptn[x].v){
if(ptn[v].cost>c+ptn[x].cost)
ptn[v].ans=ptn[u].ans*ptn[x].ans,
ptn[v].cost=c+ptn[x].cost,
q.push(make_pair(ptn[v].cost,v));
else if(ptn[v].cost==c+ptn[x].cost)
ptn[v].ans+=ptn[u].ans*ptn[x].ans;
}
}
}
return !printf("%lld %lld",ptn[0].cost,ptn[0].ans);
}
P2047 [NOI2007] 社交网络
problem
一张\((V,E)=(n,m)\)无向有边权图,定义任意一个点\(v\)的重要程度\(I(v)\):
其中\(C_{s,t}\)表示\(s,t\)两点的最短路径条数,\(C_{s,t}(v)\)表示经过\(v\)点的\(s,t\)最短路径条数。
输出每个点的重要程度。
constraint
对于 \(50\%\)的数据, \(n \le 10 , m \le 45\)
对于 \(100\%\)的数据, \(n \le 100 , m \le 4500\),任意一条边的权值 \(c\) 是正整数且 \(1 \leqslant c \leqslant 1000\)。
所有数据中保证给出的无向图连通,且任意两个结点之间的最短路径数目不超过 \(10^{10}\)
solution
数据范围不大,想到\(\operatorname{Floyd}\)。
定义\(dis(i,j)\)表示\((i,j)\)之间的最短路径,\(sum(i,j)\)表示\((i,j)\)之间最短路径的条数。
\(Floyd\)统计的时候
如果\(dis(i,k)+dis(k,j)=dis(i,j)\),说明路径相同,则\(sum(i,j)\leftarrow sum(i,j)+sum(i,k)\times sum(k,j)\)
如果\(dis(i,k)+dis(k,j)<dis(i,j)\),说明有更短路径,则\(sum(i,j)=sum(i,k)\times sum(k,j)\)
code
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
const int maxn=2e6+10;
const int mod=1e9+7;
#define int long long
#define inf 0x3f3f3f3f
int read(){
int a=0,op=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') op=-1;c=getchar();}
while(c>='0'&&c<='9') a*=10,a+=c^48,c=getchar();
return a*op;
}
int cnt,head[maxn];
struct node{int val,nxt,to;}e[maxn<<2];
void add(int u,int v,int w){
e[++cnt].nxt=head[u];
e[cnt].val=w;
e[cnt].to=v;
head[u]=cnt;
}
int n,m,u,v;
double ans,dis[101][101],sum[101][101];
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) dis[i][j]=inf;
for(int i=1;i<=m;i++){
u=read(),v=read();
dis[u][v]=dis[v][u]=read();
sum[u][v]=sum[v][u]=1;
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(i!=j&&j!=k&&i!=k){
if(dis[i][k]+dis[k][j]==dis[i][j]) sum[i][j]+=sum[i][k]*sum[k][j];
else if(dis[i][k]+dis[k][j]<dis[i][j])
dis[i][j]=dis[i][k]+dis[k][j],sum[i][j]=sum[i][k]*sum[k][j];
}
for(int k=1;k<=n;k++){
ans=0;
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
if(j!=i&&j!=k&&i!=k&&dis[i][j]==dis[i][k]+dis[k][j]) ans+=sum[i][k]*sum[k][j]/sum[i][j];
printf("%.3lf\n",ans);
}
return 0;
}
P1629 邮递员送信
problem
求有向图从\(1\)出发到每个点再返回到\(1\)的最短距离和。
constraint
对于 \(30\%\)的数据,\(1 \leq n \leq 200\)。
对于 \(100\%\)的数据,\(1 \leq n \leq 10^3,1 \leq m \leq 10^5,1\leq u,v \leq n,1 \leq w \leq 10^4\),输入保证任意两点都能互相到达。
solution
反向建边。例题。
code
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
const int maxn=1e6+10;
const int mod=1e9+7;
#define int long long
#define inf 0x3f3f3f3f3f
int read(){
int a=0,op=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') op=-1;c=getchar();}
while(c>='0'&&c<='9') a*=10,a+=c^48,c=getchar();
return a*op;
}
int cnt,head[maxn];
int cntnew,headnew[maxn];
struct node{
int to,nxt,val;
}e[maxn<<2],enew[maxn<<2];
void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].nxt=head[u];
e[cnt].val=w;
head[u]=cnt;
}
void addnew(int u,int v,int w){
enew[++cntnew].to=v;
enew[cntnew].nxt=headnew[u];
enew[cntnew].val=w;
headnew[u]=cntnew;
}
int n,m,st,x,y,z,curr,minn=inf,maxx=-inf;
int currnew;
int tot;
bool vis[maxn]={0};
int dis[maxn];
bool visnew[maxn]={0};
int disnew[maxn];
signed main(){
st=1;
n=read(),m=read();
for(int i=1;i<=n;i++) dis[i]=inf,disnew[i]=inf;
for(int i=1;i<=m;i++){
x=read(),y=read(),z=read();
add(y,x,z);
addnew(x,y,z);
}
curr=st,dis[st]=0;
while(!vis[curr]){
vis[curr]=1;
for(int i=head[curr];i;i=e[i].nxt){
int p=e[i].to;
if(!vis[p]&&dis[p]>dis[curr]+e[i].val)
dis[p]=dis[curr]+e[i].val;
}
minn=inf;
for(int i=1;i<=n;i++)
if(!vis[i]&&minn>dis[i]) minn=dis[i],curr=i;
}
currnew=st,disnew[st]=0;
while(!visnew[currnew]){
visnew[currnew]=1;
for(int i=headnew[currnew];i;i=enew[i].nxt){
int p=enew[i].to;
if(!visnew[p]&&disnew[p]>disnew[currnew]+enew[i].val)
disnew[p]=disnew[currnew]+enew[i].val;
}
minn=inf;
for(int i=1;i<=n;i++)
if(!visnew[i]&&minn>disnew[i]) minn=disnew[i],currnew=i;
}
for(int i=1;i<=n;i++) tot+=dis[i]+disnew[i];
printf("%lld",tot);
return 0;
}
P3393 逃离僵尸岛
problem
一张\((V,E)=(n,m)\)有向图中有\(K\)个点是“危险点”,与他们距离不超过\(s\)的点都属于危险区,现在从\(1\)出发走到\(n\)号店,行走到非危险区花费\(P\),行走到危险区花费\(Q\),询问最小的花费。
constraint
对于100%数据,\(2 \le N \le 100000, 1 \le M \le 200000, 0 \le K \le N - 2, 0 \le S \le 100000,1 \le P < Q \le 100000\)
solution
对于其中的危险点,我们虚拟出一个\(0\)号点连接到这若干个危险点上,之后再进行spfa。这种方法叫做虚点连边,能够优化复杂度。
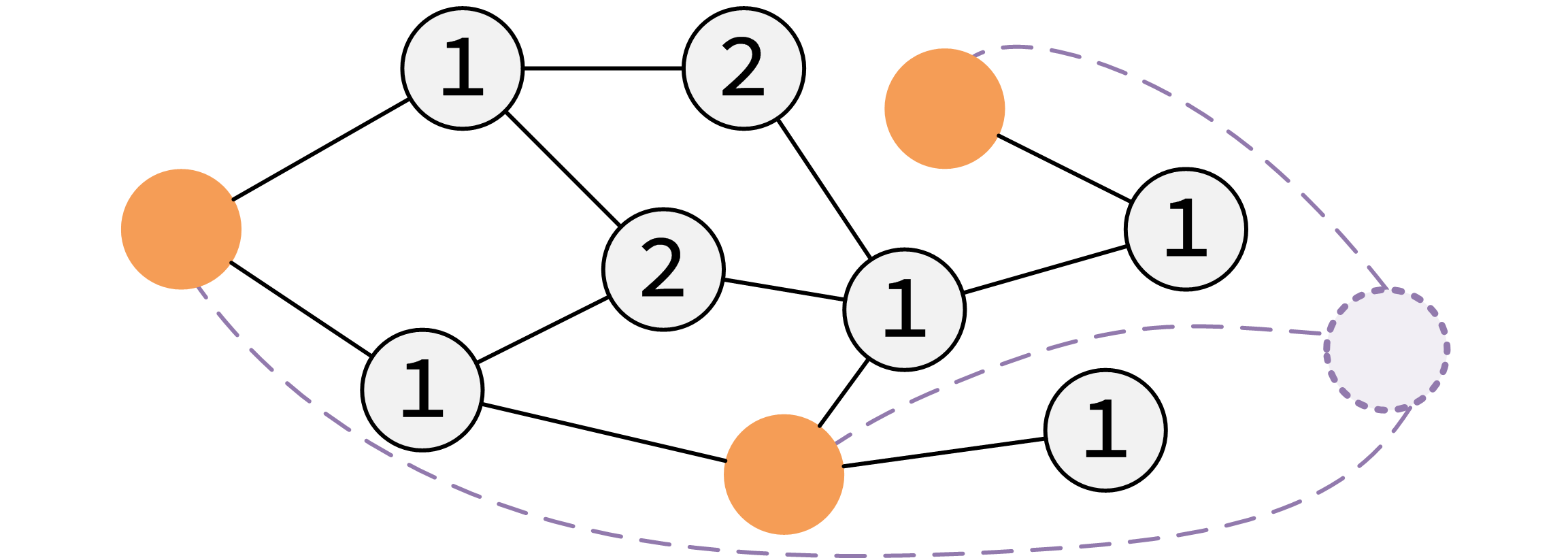
code
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
using namespace std;
const int maxn=1e6+10;
const int mod=1e9+7;
#define int long long
#define inf 0x3f3f3f3f3f
int read(){
int a=0,op=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') op=-1;c=getchar();}
while(c>='0'&&c<='9') a*=10,a+=c^48,c=getchar();
return a*op;
}
queue<int> q;
int cnt;
int dis[maxn],w[maxn<<2];
int f[maxn<<2][2],head[maxn];
bool ocp[maxn],vis[maxn],dgs[maxn];
int n,m,k,s;
int p,Q,c,a,b;
void add(int u,int v){
f[++cnt][0]=v,f[cnt][1]=head[u],head[u]=cnt;
}
void spfa(int now){
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;i++) dis[i]=inf;
while(!q.empty()) q.pop();
q.push(now),dis[now]=0,vis[now]=1;
while(!q.empty()){
int t=q.front();
for(int i=head[t];i;i=f[i][1]){
int to=f[i][0];
if(dis[to]>dis[t]+w[i]) {
dis[to]=dis[t]+w[i];
if(!vis[to]) vis[to]=1,q.push(to);
}
}
vis[t]=0,q.pop();
}
}
signed main(){
n=read(),m=read(),k=read(),s=read();
p=read(),Q=read();
for(int i=1;i<=k;i++) c=read(),ocp[c]=1;
for(int i=1;i<=m;i++){
a=read(),b=read();
if(ocp[a]&&ocp[b]) continue;
if(ocp[a]) add(0ll,b),add(b,0ll);
else if(ocp[b]) add(0ll,a),add(a,0ll);
else add(a,b),add(b,a);
}
for(int i=1;i<=cnt;i++) w[i]=1;
spfa(0);
for(int i=1;i<=n;i++) if(dis[i]<=s) dgs[i]=1;
for(int i=1;i<=cnt;i++) {
if(dgs[f[i][0]]) w[i]=Q;
else if(ocp[f[i][0]]) w[i]=inf;
else w[i]=p;
if(f[i][0]==1||f[i][0]==n) w[i]=0;
}
spfa(1);
printf("%lld",dis[n]);
return 0;
}
生成树
P1265 公路修建
problem
某国有\(n\)个城市,它们互相之间没有公路相通,因此交通十分不便。为解决这一“行路难”的问题,政府决定修建公路。修建公路的任务由各城市共同完成。
修建工程分若干轮完成。在每一轮中,每个城市选择一个与它最近的城市,申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。
政府审批的规则如下:
(1)如果两个或以上城市申请修建同一条公路,则让它们共同修建;
(2)如果三个或以上的城市申请修建的公路成环。如下图,A申请修建公路AB,B申请修建公路BC,C申请修建公路CA。则政府将否决其中最短的一条公路的修建申请;
(3)其他情况的申请一律同意。
一轮修建结束后,可能会有若干城市可以通过公路直接或间接相连。这些可以互相:连通的城市即组成“城市联盟”。在下一轮修建中,每个“城市联盟”将被看作一个城市,发挥一个城市的作用。
当所有城市被组合成一个“城市联盟”时,修建工程也就完成了。
你的任务是根据城市的分布和前面讲到的规则,计算出将要修建的公路总长度。
constraint
\(n\leqslant 5000,-10^6\leqslant x,y\leqslant 10^6\)
solution
首先考虑最小生成树的模型,唯一不同的是第二种情形。
即三个或三个以上的城市申请修建的公路成环
考虑该情形,因为修路的申请是申请离它最近的城市,所以上述条件实质上为
“存在三个或三个以上的城市,他们两两间的最近城市连起来成环”
显然这样的情形是不存在的。
剩下就是简单的最小生成树问题。
本题另外一个问题在于空间的限制上, \(5000\times 5000\)的空间大小会MLE
那么我们发现题目给的是坐标,所以我们想到可以不直接存储距离,而是在Prim的运行流程中把距离即时计算出来即可。
code
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
#include <vector>
using namespace std;
const int maxn=1e6+10;
const int maxm=5e5+10;
const int mod=1e9+7;
#define int long long
#define inf 0x3f3f3f3f3f
int read(){
int a=0,op=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') op=-1;c=getchar();}
while(c>='0'&&c<='9') a*=10,a+=c^48,c=getchar();
return a*op;
}
struct node{
int x,y;
}poi[maxn];
double ans,dis[maxn];
bool vis[maxn];
int n,pos;
double calc(int a,int b){
return sqrt((double)(poi[a].x-poi[b].x)*(poi[a].x-poi[b].x)+(double)(poi[a].y-poi[b].y)*(poi[a].y-poi[b].y));
}
signed main(){
n=read();
for(int i=1;i<=n;i++) poi[i].x=read(),poi[i].y=read(),dis[i]=inf;
pos=0,dis[1]=0;
for(int i=1;i<=n;i++){
double minn=inf;
for(int j=1;j<=n;j++) if(!vis[j]&&dis[j]<minn) minn=dis[j],pos=j;
ans+=minn,vis[pos]=1;
for(int j=1;j<=n;j++){
double d=calc(pos,j);
if(d<dis[j]) dis[j]=d;
}
}
printf("%.2lf\n",ans);
}
P1991 无线通讯网
problem
国防部计划用无线网络连接若干个边防哨所。2 种不同的通讯技术用来搭建无线网络;
每个边防哨所都要配备无线电收发器;有一些哨所还可以增配卫星电话。
任意两个配备了一条卫星电话线路的哨所(两边都ᤕ有卫星电话)均可以通话,无论他们相距多远。而只通过无线电收发器通话的哨所之间的距离不能超过 \(D\),这是受收发器的功率限制。收发器的功率越高,通话距离 \(D\) 会更远,但同时价格也会更贵。
收发器需要统一购买和安装,所以全部哨所只能选择安装一种型号的收发器。换句话说,每一对哨所之间的通话距离都是同一个 \(D\)。你的任务是确定收发器必须的最小通话距离 \(D\),使得每一对哨所之间至少有一条通话路径(直接的或者间接的)。
constraint
对于 \(20\%\) 的数据:\(P = 2,S = 1\)
对于另外 \(20\%\) 的数据:\(P = 4,S = 2\)
对于 \(100\%\) 的数据保证:\(1 ≤ S ≤ 100,S < P ≤ 500,0 ≤ x,y ≤ 10000\)。
solution
做本题首先应该知道一共有\(p\)个点就是树有\(p-1\)条边,有\(s\)个卫星电话就是不用连接最大的\(s-1\)条边。
因为数据范围小,本题适用kruskal。存储每条边的权值和两端进行排序。
但本题最重要的部分是卫星电话,由前文便可只本题一共只需要树中前\((p-s)\)条边里的最大边即可,剩下的边用卫星电话。
code
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
#include <vector>
using namespace std;
const int maxn=1e6+10;
const int maxm=5e5+10;
const int mod=1e9+7;
#define int long long
#define inf 0x3f3f3f3f3f
int read(){
int a=0,op=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') op=-1;c=getchar();}
while(c>='0'&&c<='9') a*=10,a+=c^48,c=getchar();
return a*op;
}
struct node{
int t1,t2;double v;
}lin[maxn];
struct node2{
double x,y;
}st[maxn];
int s,p,num,fa[maxn];
double ans=-1.0;
double dis(int x1,int y1){
return sqrt((st[x1].x-st[y1].x)*(st[x1].x-st[y1].x)
+(st[x1].y-st[y1].y)*(st[x1].y-st[y1].y));
}
bool cmp(node x,node y){
return x.v<y.v;
}
int find(int x){
return fa[x]==x?x:fa[x]=find(fa[x]);
}
void uni(int x,int y){
fa[find(x)]=find(y);
}
double fread(){
double x;
scanf("%lf",&x);
return x;
}
bool check(int x,int y){
if(fa[find(x)]==find(y)) return 1;
return 0;
}
signed main(){
s=read(),p=read();
for(int i=1;i<=p;i++) fa[i]=i;
for(int i=1;i<=p;i++) st[i].x=fread(),st[i].y=fread();
for(int i=1;i<=p;i++)
for(int j=i+1;j<=p;j++)
num++,lin[num].t1=i,lin[num].t2=j,lin[num].v=dis(i,j);
sort(lin+1,lin+num+1,cmp);
int a,b;
s=p-s;
for(int i=1;i<=num,s>0;i++){
a=lin[i].t1,b=lin[i].t2;
if(!check(a,b)) uni(a,b),s--,ans=max(ans,lin[i].v);
}
printf("%.2lf\n",ans);
return 0;
}
problem
constraint
solution
code


 浙公网安备 33010602011771号
浙公网安备 33010602011771号