NOI contest#1

1

problem

给定一个序列\(A\)，定义一个区间 \([l,r]\)的最大子段和为\([l,r]\) 的一段连续子区间的和，满足其为 \([l,r]\)所有连续子区间和中最大的一个。

求出所有 \(1\le l\le r\le n\)的区间 \([l,r]\) 的最大子段和的和，答案对 \(2^{64}\)取模。

具体来说，假设答案为 \(x\)，你需要输出最小的非负整数 \(y\)，满足 \(x\) 和 \(y\) 对 \(2^{64}\)同余。

constraint

对于 \(30\%\)的数据，满足 \(1 \le n \le 1000\)。

对于另外 \(20\%\)的数据，满足 \(0 \le A_i\)
对于 \(100\%\)的数据，满足 \(1 \le n \le 10^5,-10^9 \le A_i \le 10^9\)

solution

30pts:\(O(n^2)\),枚举左端点，然后for右端点，维护所有子区间的最大子段和
50pts:\(O(n)\)
当所有数非负时，最大子段和会包含整个区间
一个在\(i\)位置的数\(a[i]\)被\(i(n-i+1)\)个区间包含，贡献为\(a[i]\times i\times (n-i+1)\)
算出所有位置的贡献
100pts:
考虑对序列进行分治
每次考虑跨过分治中线的左边的后缀和右边的前缀拼起来的贡献
假设两部分分别是A,B
A+B的最大子段和是max(max(A的最大子段和,B的最大子段和),A的最大后缀和+B的最大前缀和))

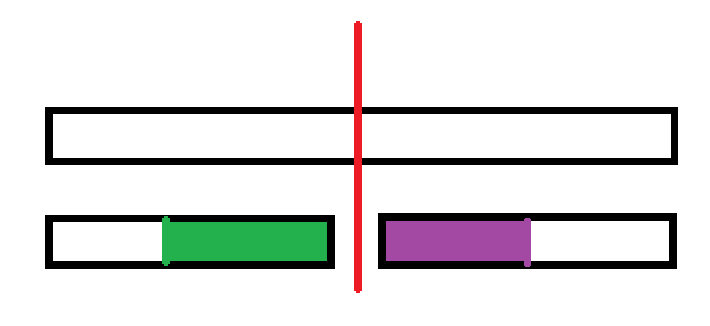
分类讨论一下
如果A的最大子段和最大，设其为\(x\)，设其最大后缀和为\(y\)，则需要找的是B的最大子段和\(\leqslant x\)，且最大前缀和\(\leqslant x-y\)的B个数
这个可以对B的最大子段和排序后，离散化后可以使用树状数组维护，或者直接平衡树维护
B的最大子段和最大同理
分类讨论一下
在其他情况中，则是对于A，找出不满足上述两种情况的B的最大前缀和的和，使用类似的数据结构维护即可

\(O(n\log^2n)\)

code

//std

2

problem

constraint

solution

code

3

problem

constraint

solution

code