排序算法之堆排序

完全二叉树：

　　完全二叉树指的是除最后一层外，其余各层都是满的，而最后一层的节点从左到右是不间断的。满二叉树属于一种特殊的完全二叉树。

          

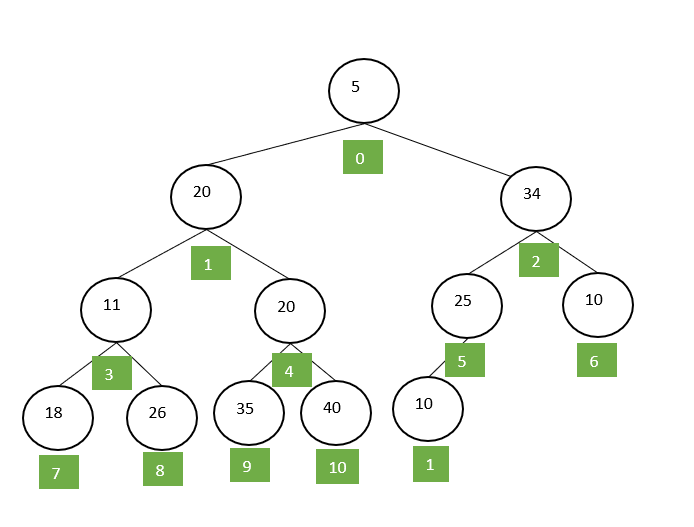
 堆：

　　堆简单的来讲，物理结构是一维数组，而逻辑结构是完全二叉树。堆又分为小顶堆和大顶堆，小顶堆指的是每个节点的值都小于或等于其左右孩子节点的值，大顶堆指的是每个节点的值都大于或等于其左右孩子节点的值。

      

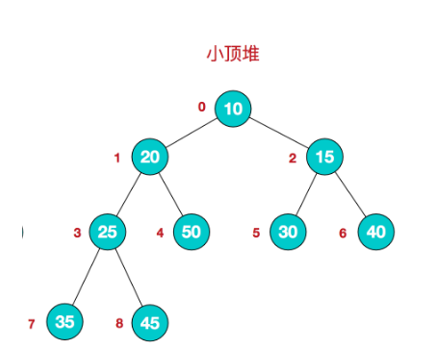
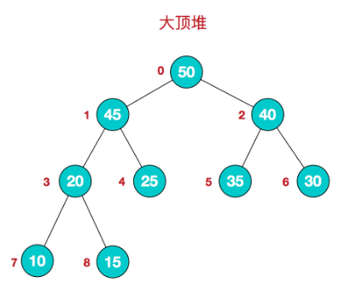
 堆排序：

　　堆排序是利用堆这种数据结构而设计的一种排序算法，求升序用大顶堆，求降序用小顶堆。

堆排序的思路：

　　现在有一个待排序的数组，我们将它看作是逻辑结构上的完全二叉树，如图所示：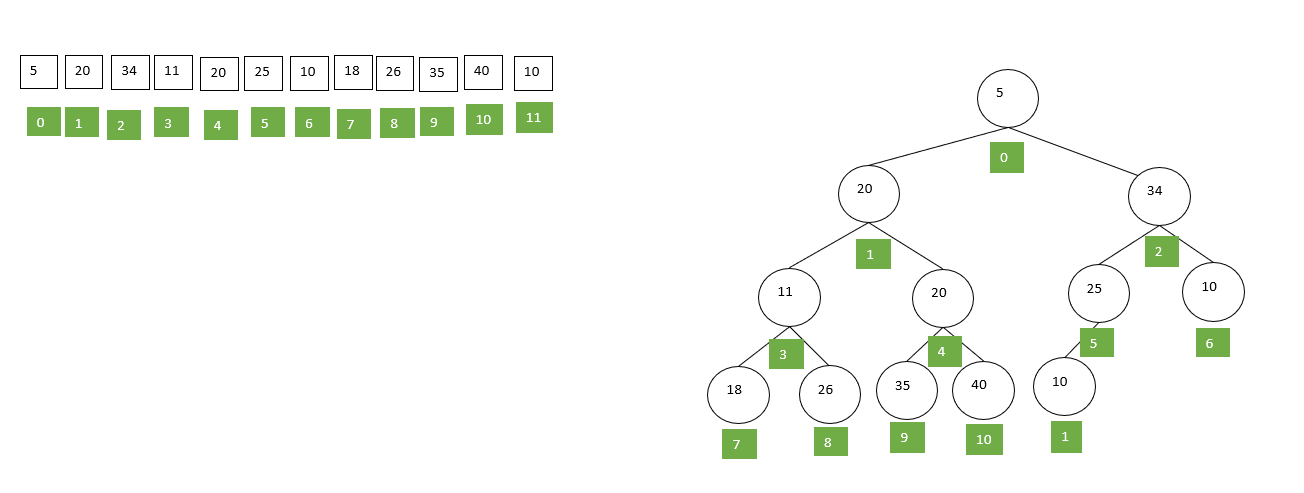 　　

　　如何将完全二叉树调整成大顶堆：

　　第一步：

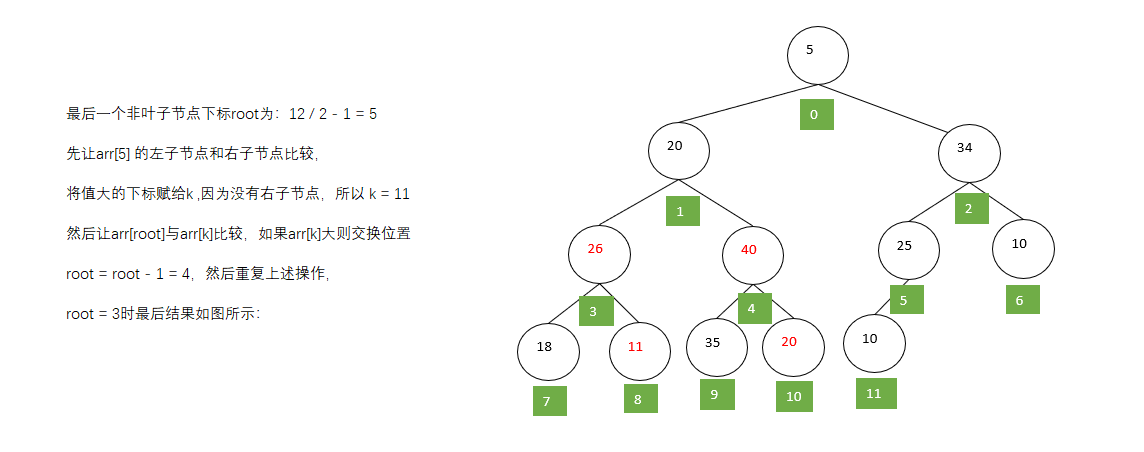
　　第二步：

 

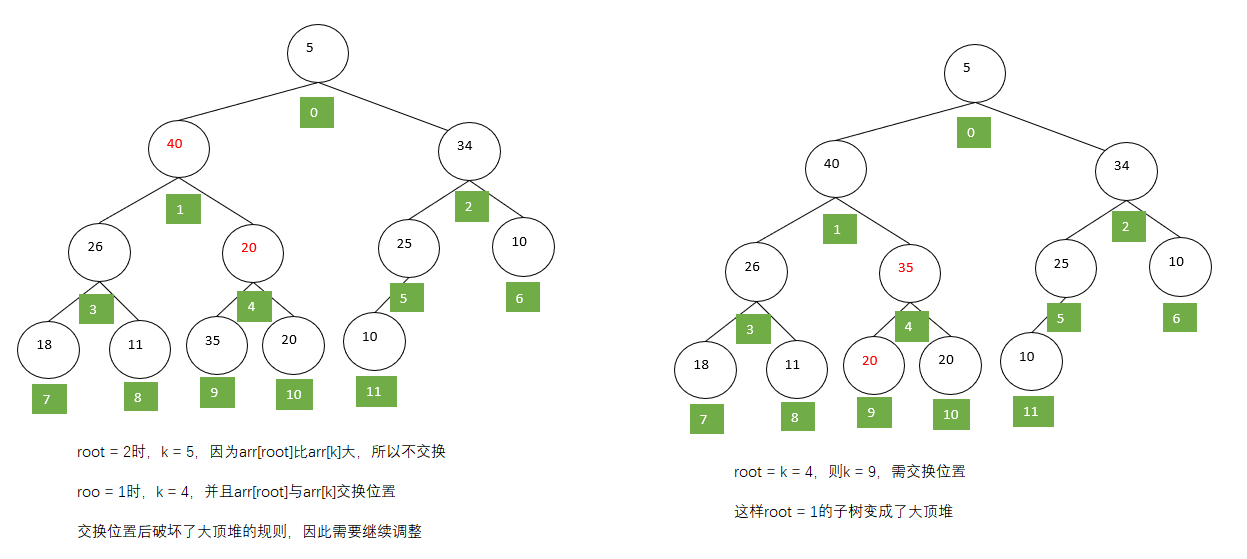
　　第三步：

  

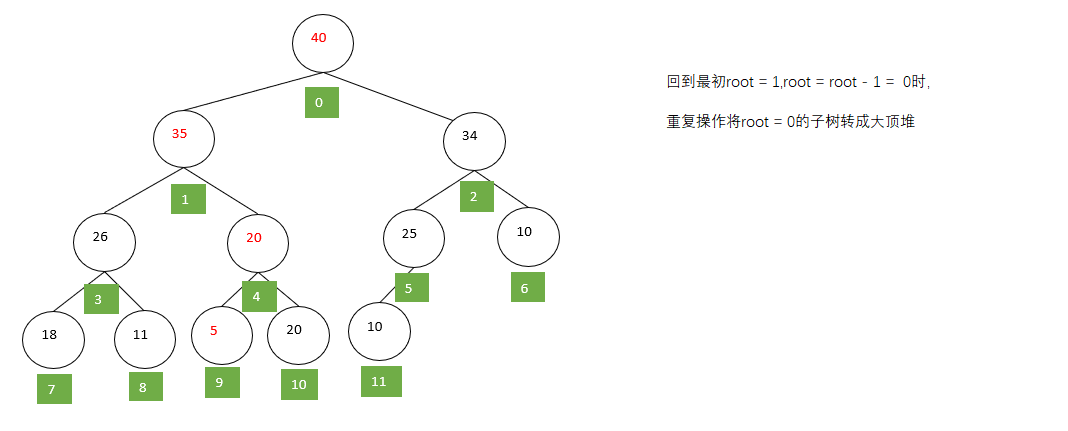
　　具体的排序步骤：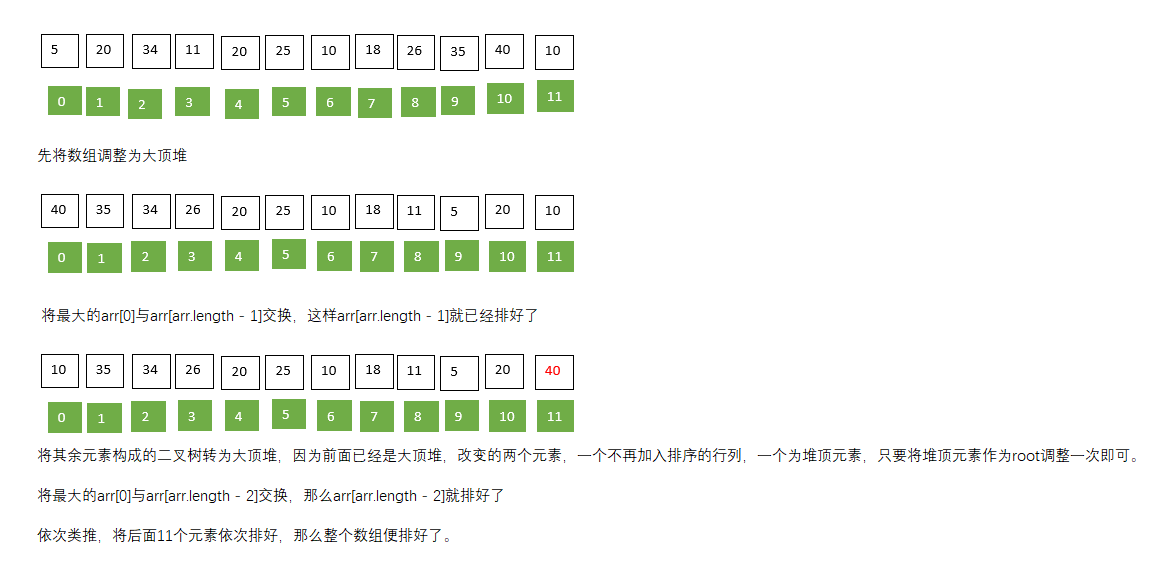 

代码：

    /**
     * 堆排序
     * @param arr
     */
    public static void heapSort(int[] arr) {
        //将物理数组构成的逻辑二叉树转为大顶堆
        for (int root = arr.length / 2 - 1; root >= 0; root--) {
            largeTopHeap(arr, root, arr.length);
        }
        for (int i = arr.length - 1; i > 0; i--) {
            //将最大的堆顶元素与arr[i]交换
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
            //arr[i]不再参与排序,需排序的数组长度为i，
            //只需将堆顶元素作为root调整一次,那么整个需排序数组构成的二叉树就是大顶堆
            largeTopHeap(arr, 0, i);
        }
    }

    /**
     * 将以root为根节点的二叉树调整为大顶堆
     * @param arr 以数组形式存储的二叉树
     * @param root 目标二叉树的根节点
     * @param length 未排序的长度
     */
    private static void largeTopHeap(int[] arr, int root, int length) {
        for (int k = 2 * root + 1; k < length; k = 2 * k + 1) {
            //左子节点与右子节点的值进行比较，大的把下标赋给k
            if (k + 1 < length && arr[k + 1] > arr[k]) {
                k++;
            }

            if (arr[k] > arr[root]) {
                //如果arr[k] > arr[root]，则交换位置
                int temp = arr[root];
                arr[root] = arr[k];
                arr[k] = temp;
                //以k为根节点的子树需要继续调整
                root = k;
            } else {
                //不需要交换说明root的子树已经是大顶堆
                break;
            }
        }
    }