树状数组(Binary Indexed Tree) 总结

1.“树状数组”数据结构的一种应用

　　对含有n个元素的数组(a[1],...,a[k],...,a[n])：

　　(1)求出第i个到第j个元素的和，sum=a[i]+...+a[j]。

　　　　进行j-i+1次加法，复杂度为O(j-i+1)

　　(2)任意修改其中某个元素的值。

　　　　使用数组下标可以直接定位修改，时间复杂度为O(1)

 　　对于同时支持上述两种操作的系统中，求和操作(1)求任意连续个数组元素和的平均时间复杂度为O(n)，修改操作(2)时间复杂度是O(1)。如果系统中大量进行上述两种操作m次，其中执行操作(1)概率1/p，操作(2)概率1-1/p，则系统时间复杂度为：

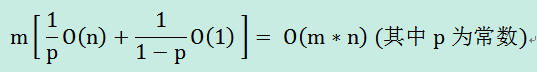
　　可以使用树状数组使得上述两种操作的时间复杂度为O(m*logn)。

2.树状数组介绍

　　核心思想：

　　　　(1)树状数组中的每个元素是原数组中一个或者多个连续元素的和。

　　　　(2)在进行连续求和操作a[1]+...+a[n]时，只需要将树状数组中某几个元素的和即可。时间复杂度为O(lgn)

　　　　(3)在进行修改某个元素a[i]时，只需要修改树状数组中某几个元素的和即可。时间复杂度为O(lgn)

　　下图就是一个树状数组的示意图：

　　解释如下：

　　1)　a[]: 保存原始数据的数组。(操作(1)求其中连续多个数的和，操作(2)任意修改其中一个元素)

　　　　e[]: 树状数组，其中的任意一个元素e[i]可能是一个或者多个a数组中元素的和。如e[2]=a[1]+a[2]; e[3]=a[3]; e[4]=a[1]+a[2]+a[3]+a[4]。 

　　2） e[i]是几个a数组中的元素的和？

　　　　如果数字 i 的二进制表示中末尾有k个连续的0，则e[i]是a数组中2^k个元素的和，则e[i]=a[i-2^k+1]+a[i-2^k+2]+...+a[i-1]+a[i]。

　　　　如：4=100(2)　　e[4]=a[1]+a[2]+a[3]+a[4];

　　　　　　6=110(2)　　e[6]=a[5]+a[6]

　　　　　　7=111(2)　　e[7]=a[7]

　　3)　后继：可以理解为节点的父亲节点。是离它最近的，且编号末位连续0比它多的就是它的父亲,如e[2]是e[1]的后继；e[4]是e[2]的后继。

　　　　　　如e[4] = e[2]+e[3]+a[4] = a[1]+a[2]+a[3]+a[4] ，e[2]、e[3]的后继就是e[4]。

　　　　　　后继主要是用来计算e数组，将当前已经计算出的e[i]添加到他们后继中。

　　　　前驱：节点前驱的编号即为比自己小的，最近的，最末连续0比自己多的节点。如e[7]的前驱是e[6],e[6]的前驱是e[4]。

 　　　　　  前驱主要是在计算连续和时，避免重复添加元素。

　　　　　　如：Sum(7)=a[1]+...+a[7]=e[7]+e[6]+e[4]。(e[7]的前驱是e[6], e[6]的前驱是e[4])

　　　　计算前驱与后继：

　　　　　　lowbit(i) = ( (i-1) ^ i) & i ;

　　　　　　节点e[i]的前驱为 e[ i - lowbit(i) ]；

　　　　　　节点e[i]的前驱为 e[ i + lowbit(i) ]

3.树状数组代码示例

#include <iostream>
#include <stdio.h>

using namespace std;

int input(int*,int*,int);    ///输入数据
int calStageSum(int*,int);    ///计算树状数组
int getSum(int*,int);    ///求出前n个数字的和
int updataElement(int*,int*,int,int,int);    ///更新某一位置上的元素

int main (){
    int n;
    int newValue;
    cout<<"Input the n(n>3) :";
    cin>>n;

    int *num = new int[n+1];
    int *sum = new int[n+1];

    cout<<"Input "<<n<<" numbers"<<endl;
    input(num,sum,n);
    calStageSum(sum,n);

    cout<<"The sum of first three number:"<<getSum(sum,3)<<endl;

    cout<<"Update the 2nd number value:";
    cin>>newValue;
    updataElement(sum,num,n,2,newValue);

    cout<<"The sum of first three number:"<<getSum(sum,3)<<endl;

    delete []num;
    delete []sum;
    return 0;
}

int input(int* num,int *sum,int n){
    for(int i=1;i<=n;i++){
        cin>>num[i];
        sum[i] = num[i];
    }
    return 0;
}

int calStageSum(int *sum,int n){
    int lowbit;
    int par;
    for(int i=1;i<=n;i++){
        lowbit = ((i-1)^i)&i;
        par = lowbit+i;   ///后继节点id
        if(par <= n){
            sum[par] = sum[par] + sum[i];
        }
    }
    return 0;
}

int getSum(int* sum,int n){
    int sumPreN = 0;
    int lowbit  = 0;
    while(n!=0){
        sumPreN += sum[n];
        lowbit = ((n-1)^n)&n;
        n = n - lowbit; ///前驱节点id
    }
    return sumPreN;
}

int updataElement(int* sum,int *num,int n,int pos,int newvalue){
    int lowbit = 0;
    int dis = newvalue - num[pos];
    num[pos] = newvalue;
    sum[pos] = sum[pos]+dis;

    while(true){
        lowbit = ((pos-1)^pos)&pos;
        pos = pos + lowbit; ///后继节点id
        if(pos <= n){
            sum[pos] = sum[pos]+dis;
        }
        else
            break;
    }
    return 0;
}